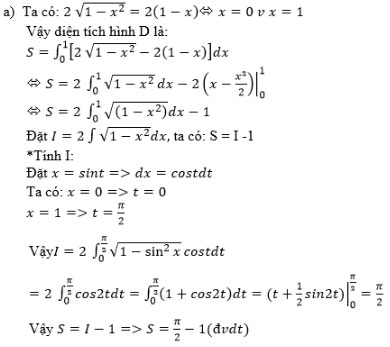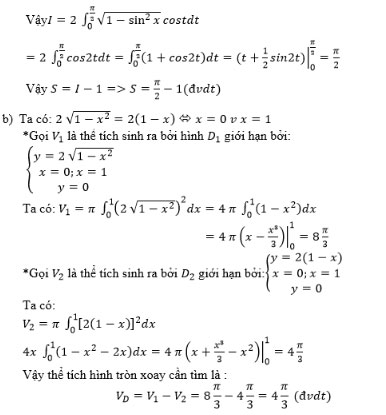Giải bài tập Toán 12 ôn tập chương 3: Nguyên hàm - Tích phân và ứng dụng

Bài tập Toán 12 Giải tích ôn tập chương 3

Để giúp các bạn học sinh học tập hiệu quả hơn môn Toán, VnDoc.com đã tổng hợp bộ câu hỏi ôn tập chương 3 Giải tích kèm theo đáp án giúp các bạn rèn luyện giải bài tập một cách nhanh và chính xác nhất. Mời các bạn học sinh và thầy cô tham khảo.

Giải bài tập Toán 12 ôn tập chương 3: Nguyên hàm - Tích phân và ứng dụng

Bài 1 (trang 126 SGK Giải tích 12):

a) Phát biểu định nghĩa nguyên hàm của hàm số f(x) trên một khoảng.

b) Nêu phương pháp tính nguyên hàm từng phần. Cho ví dụ minh họa.

Lời giải:

a) Cho hàm số f(x) xác định trên K ( k là nửa khoảng hay đoạn của trục số). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x)=f(x) với mọi x thuộc K.

Định lý: Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì:

- Với mỗi hằng số C, F(x) + C cũng là một nguyên hàm của hàm số trên f(x) trên K.

- G(x) cũng là một nguyên hàm của hàm số f(x) trên K thì tồn tại một hằng số C sao cho G(x) = F (x) +C

b)

*Đổi biên số:

Nếu ∫f(u)du=F(u)+C va u(x) là hàm số có đạo hàm liên tục thì:

∫f(ux) u'(x)dx=F(u(x))+C

*Tính nguyên hàm từng phần:

Nếu hai hàm số u= u(x) và v = v(x) có đạo hàm liên tục trên K thì:

∫u(x) v'(x)dx=u(x)v(x)- ∫v(x) u'(x)dx

Hay ∫udv=uv- ∫vdv.

Ví dụ:

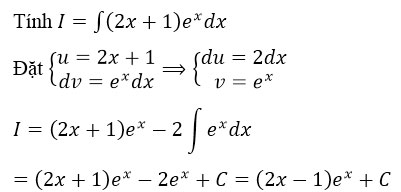
Bài 2 (trang 126 SGK Giải tích 12):

a) Phát biểu định nghĩa tích phân của hàm số f(x) trên một đoạn.

b) Nêu các tính chất của tích phân. Cho ví dụ minh họa.

Lời giải:

Bài 3 (trang 126 SGK Giải tích 12): Tìm nguyên hàm của các hàm số sau:

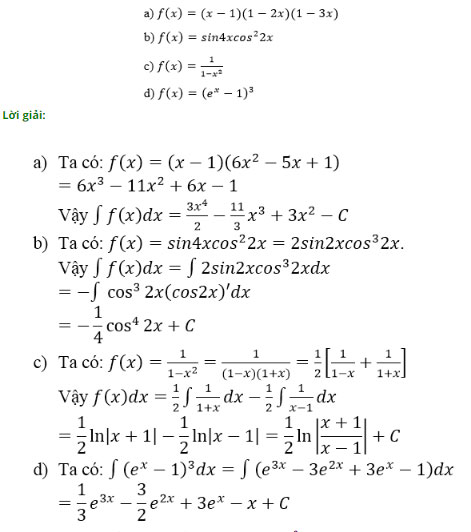
Bài 4 (trang 126 SGK Giải tích 12): Tính:

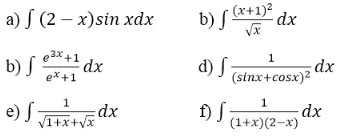
Lời giải

Bài 5 (trang 127 SGK Giải tích 12): Tính:

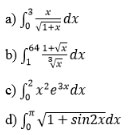
Lời giải

Bài 6 (trang 127 SGK Giải tích 12): Tính:

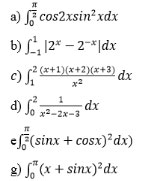
Lời giải

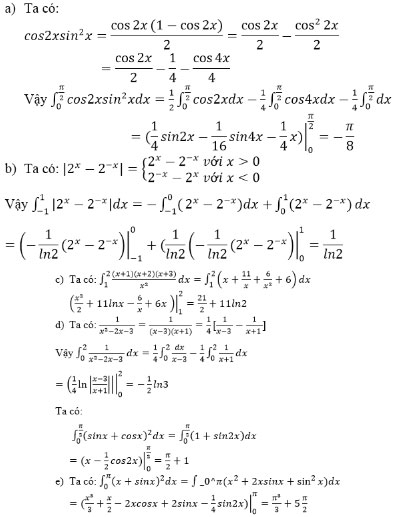
Bài 7 (trang 127 SGK Giải tích 12): Xét hình phẳng D giới hạn bởi y=2√(1-x2 ) và y=2(1-x)

a) Tính diện tích hình D

b) Quay hình D xung quanh trục Ox. Tính thể tích khối tròn xoay được tạo thành.

Lời giải: