Giải vở bài tập Đại số lớp 12 bài 2: Cực trị của hàm số
Giải vở bài tập Đại số lớp 12 bài 2
Mời các bạn học sinh tham khảo tài liệu: Giải vở bài tập Đại số lớp 12 bài 2: Cực trị của hàm số, tài liệu đã được VnDoc.com cập nhật và kèm theo cách giải bài tập Toán 12 chi tiết sẽ giúp các bạn học sinh học tốt môn Toán lớp 12. Mời các bạn học sinh và thầy cô cùng tham khảo.
Giải vở bài tập Đại số lớp 12 bài 1: Sự đồng biến, nghịch biến của hàm số
Lý thuyết Toán 12 chương 1: Cực trị của hàm số
Giải vở bài tập Đại số lớp 12 bài 2: Cực trị của hàm số
Bài 1.11 trang 15 Sách bài tập (SBT) Giải tích 12
a) 
\(y = - 2{x^2} + 7x - 5\)
b) \(y = {x^3} - 3{x^2} - 24x + 7\)
c) \(y = {x^4} - 5{x^2} + 4\)
d) \(y = {(x + 1)^3}(5 - x)\)
e) \(y = {(x + 2)^2}{(x - 3)^3}\)
Hướng dẫn làm bài:
a) \(y = - 2{x^2} + 7x - 5\). TXĐ: R
\(y' = - 4x + 7,y' = 0 < = > x = {7 \over 4}\)\(y'' = - 4 = > y''({7 \over 4}) = - 4 < 0\)
Vậy \(x = {7 \over 4}\) là điểm cực đại của hàm số và \({y_{CD}} = {9 \over 8}\)
b) \(y = {x^3} - 3{x^2} - 24x + 7\) . TXĐ: R
\(y' = 3{x^2} - 6x - 24 = 3({x^2} - 2x - 8)\)
\(y' = 0 \Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 4 \hfill \cr} \right.\)
Vì \(y''( - 2) = - 18 < 0,y''(4) = 18 > 0\) nên hàm số đạt cực đại tại x = - 2 ; đạt cực tiểu tại x = 4 và yCĐ = y(-2) = 35 ; yCT = y(4) = -73.
c) \(y = {x^4} - 5{x^2} + 4\)
TXĐ: R
\(= {{2{x^2} - 2{m^2} - {x^2} - 2mx + 3} \over {{{(x - m)}^2}}} = {{{x^2} - 2mx - 2{m^2} + 3} \over {{{(x - m)}^2}}}\)\(y' = 4{x^3} - 10x = 2x(2{x^2} - 5)\)
\(y' = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = - \sqrt {{5 \over 2}} \hfill \cr
x = \sqrt {{5 \over 2}} \hfill \cr} \right.\)
Vì \(y''( \pm \sqrt {{5 \over 2}} ) = 20 > 0,y''(0) = - 10 < 0\)
Nên hàm số đạt cực đại tại x = 0, đạt cực tiểu tại \(x = \pm \sqrt {{5 \over 2}}\) và ta có:
\(yCĐ = y(0) = 4 , {y_{_{CT}}} = y( \pm \sqrt {{5 \over 2}} ) = - {9 \over 4}\)
d) TXĐ: R
\(y' = - {(x + 1)^3} + 3{(x + 1)^2}(5 - x) = 2{(x + 1)^2}(7 - 2x)\)
\(y' = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr
x = {7 \over 2} \hfill \cr} \right.\)
Bảng biến thiên:
Hàm số đạt cực đại tại \(x = {7 \over 2};{y_{CD}} = y({7 \over 2}) = {{2187} \over {16}}\)
e) TXĐ: R
\(y' = 2(x + 2){(x - 3)^3} + 3{(x + 2)^2}{(x - 3)^2} = 5x(x + 2){(x - 3)^2}\)
\(y' = 0 \Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 0 \hfill \cr
x = 3 \hfill \cr} \right.\)
Bảng biến thiên:
Từ đó suy ra yCĐ = y(-2) = 0 ; yCT = y(0) = -108.
Bài 1.12 trang 15 Sách bài tập (SBT) Giải tích 12
Tìm cực trị của các hàm số sau:
a) \(y = {{x + 1} \over {{x^2} + 8}}\)
b) \(y = {{{x^2} - 2x + 3} \over {x - 1}}\)
c) \(y = {{{x^2} + x - 5} \over {x + 1}}\)
d) \(y = {{{{(x - 4)}^2}} \over {{x^2} - 2x + 5}}\)
Hướng dẫn làm bài:
a) TXĐ: R
\(y' = {{{x^2} + 8 - 2x(x + 1)} \over {{{({x^2} + 8)}^2}}} = {{ - {x^2} - 2x + 8} \over {{{({x^2} + 8)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \matrix{
x = - 4 \hfill \cr
x = 2 \hfill \cr} \right.\)
Bảng biến thiên:
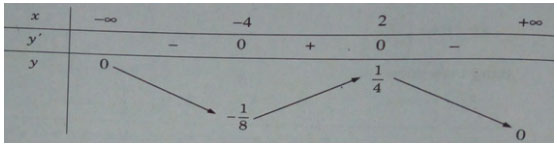
Hàm số đạt cực đại tại x = 2, cực tiểu tại x = - 4 và \({y_{CD}} = y(2) = {1 \over 4};{y_{CT}} = y( - 4) = - {1 \over 8}\)
b) Hàm số xác định và có đạo hàm với mọi x ≠ 1.
\(y' = {{{x^2} - 2x - 1} \over {{{(x - 1)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \matrix{
x = 1 - \sqrt 2 \hfill \cr
x = 1 + \sqrt 2 \hfill \cr} \right.\)
Bảng biến thiên:
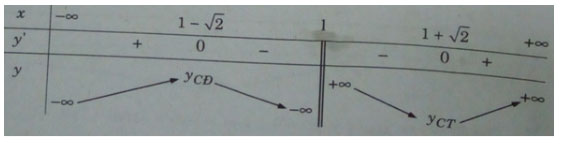
Hàm số đạt cực đại tại \(x = 1 - \sqrt 2\) và đạt cực tiểu tại \(x = 1 + \sqrt 2\), ta có:
\({y_{CD}} = y(1 - \sqrt 2 ) = - 2\sqrt 2 ;{y_{CT}} = y(1 + \sqrt 2 ) = 2\sqrt 2\)
c) TXĐ: R\{-1}
\(y' = {{{x^2} + 2x + 6} \over {{{(x + 1)}^2}}} > 0,\forall x \ne - 1\)
Hàm số đồng biến trên các khoảng và do đó không có cực trị.
d) \(y = {{{{(x - 4)}^2}} \over {{x^2} - 2x + 5}}\)
Vì x2 – 2x + 5 luôn luôn dương nên hàm số xác định trên \(( - \infty ; + \infty )\)
\(y' = {{2(x - 4)({x^2} - 2x + 5) - {{(x - 4)}^2}(2x - 2)} \over {{{({x^2} - 2x + 5)}^2}}} = {{2(x - 4)(3x + 1)} \over {{{({x^2} - 2x + 5)}^2}}}\)
\(y' = 0 \Leftrightarrow \left[ \matrix{
x = - {1 \over 3} \hfill \cr
x = 4 \hfill \cr} \right.\)
Bảng biến thiên:
Hàm số đạt cực đại tại \(x = - {1 \over 3}\), đạt cực tiểu tại x = 4 và \({y_{CD}} = y( - {1 \over 3}) = {{13} \over 4};{y_{CT}} = y(4) = 0\)
Bài 1.13 trang 15 Sách bài tập (SBT) Giải tích 12
Tìm cực trị của các hàm số sau:
a) \(y = x - 6\root 3 \of {{x^2}}\)
b) \(y = (7 - x)\root 3 \of {x + 5}\)
c) \(y = {x \over {\sqrt {10 - {x^2}} }}\)
d) \(y = {{{x^3}} \over {\sqrt {{x^2} - 6} }}\)
Hướng dẫn làm bài:
a) TXĐ: R
\(y' = 1 - {4 \over {\root 3 \of x }} = {{\root 3 \of x - 4} \over {\root 3 \of x }}\)
\(y' = 0 < = > x = 64\)
Bảng biến thiên:
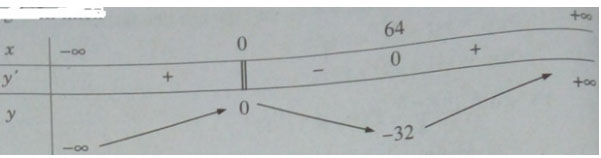
Vậy ta có yCĐ = y(0) = 0 và yCT = y(64) = -32.
b) Hàm số xác định trên khoảng \((−∞;+∞)(−∞;+∞).\)
\(y' = - \root 3 \of {x + 5} + {{7 - x} \over {3\root 3 \of {{{(x + 5)}^2}} }} = {{ - 4(x + 2)} \over {3\root 3 \of {{{(x + 5)}^2}} }}\)
Bảng biến thiên:
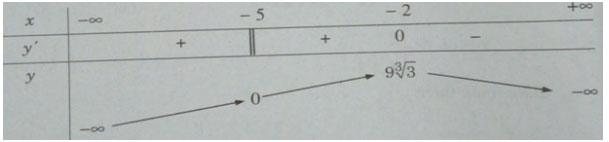
Vậy \({y_{CD}} = y( - 2) = 9\root 3 \of 3\)
c) Hàm số xác định trên khoảng \(( - \sqrt {10} ;\sqrt {10} )\)
\(y' = {{\sqrt {10 - {x^2}} + {{{x^2}} \over {\sqrt {10 - {x^2}} }}} \over {10 - {x^2}}} = {{10} \over {(10 - {x^2})\sqrt {10 - {x^2}} }}\)
Vì y’ > 0 với mọi \(( - \sqrt {10} ;\sqrt {10} )\) nên hàm số đồng biến trên khoảng đó và do đó không có cực trị.
d) TXĐ: \(D = ( - \infty ; - \sqrt 6 ) \cup (\sqrt 6 ; + \infty )\)
\(y' = {{3{x^2}\sqrt {{x^2} - 6} - {{{x^4}} \over {\sqrt {{x^2} - 6} }}} \over {{x^2} - 6}}\)\(= {{3{x^2}({x^2} - 6) - {x^4}} \over {\sqrt {{{({x^2} - 6)}^3}} }}\)\(= {{2{x^2}({x^2} - 9)} \over {\sqrt {{{({x^2} - 6)}^3}} }}\)
Bảng biến thiên:
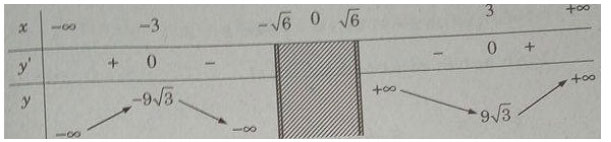
Từ đó ta thấy hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x =- 3 và \({y_{CT}} = y(3) = 9\sqrt 3 ;{y_{CD}} = y( - 3) = - 9\sqrt 3\)
Bài 1.14 trang 15 Sách bài tập (SBT) Giải tích 12
a) \(y = \sin 2x\)
b) \(y = \cos x - \sin x\)
c) \(y = {\sin ^2}x\)
Hướng dẫn làm bài:
a) \(y = \sin 2x\)
Hàm số có chu kỳ \(T = \pi\)
Xét hàm số \(y = \sin 2x\) trên đoạn \({\rm{[}}0;\pi {\rm{]}}\), ta có:
\(y' = 2\cos 2x\)
\(y = 0 \Leftrightarrow \left[ \matrix{
x = {\pi \over 4} \hfill \cr
x = {{3\pi } \over 4} \hfill \cr} \right.\)
Bảng biến thiên:
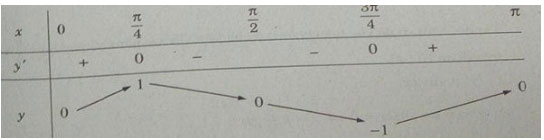
Do đó trên đoạn \({\rm{[}}0;\pi {\rm{]}}\), hàm số đạt cực đại tại \({\pi \over 4}\), đạt cực tiểu tại \({{3\pi } \over 4}\) và \({y_{CD}} = y({\pi \over 4}) = 1;\,\,{y_{CT}} = y({{3\pi } \over 4}) = - 1\)
Vậy trên R ta có:
\({y_{CĐ}} = y({\pi \over 4} + k\pi ) = 1;\)
\({y_{CT}} = y({{3\pi } \over 4} + k\pi ) = - 1,k \in Z\)
b)
Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn \({\rm{[}} - \pi ;\pi {\rm{]}}\)
\(y' = - \sin x - \cos x\)\(y' = 0 < => \tan x = - 1 < = > x = - {\pi \over 4} + k\pi ,k \in Z\)
Lập bảng biến thiên trên đoạn [−π;π]
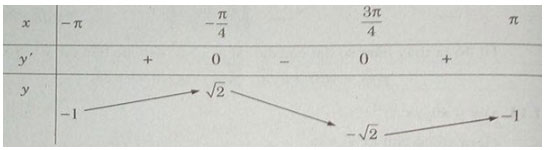
Hàm số đạt cực đại tại \(x = - {\pi \over 4} + k2\pi\), đạt cực tiểu tại \(x = {{3\pi } \over 4} + k2\pi (k \in Z)\) và
\({y_{CĐ}} = y( - {\pi \over 4} + k2\pi ) = \sqrt 2 ;\)
\({y_{CT}} = y({{3\pi } \over 4} + k2\pi ) = - \sqrt 2 (k \in Z)\)
c) Ta có: \(y = {\sin ^2}x = {{1 - \cos 2x} \over 2}\)
Do đó, hàm số đã cho tuần hoàn với chu kỳ \(\pi\). Ta xét hàm số \(y = {1 \over 2} - {1 \over 2}\cos 2x\) trên đoạn \({\rm{[}}0;\pi {\rm{]}}\).
\(y' = \sin 2x\)\(y' = 0 < = > \sin 2x = 0 < = > x = k.{\pi \over 2}(k \in Z)\)
Lập bảng biến thiên trên đoạn \(\left[ {0,\pi } \right]\)
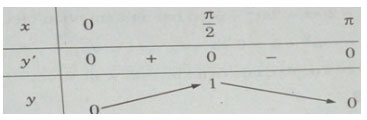
Từ đó, ta thấy hàm số đạt cực tiểu tại \(x = k.{\pi \over 2}\) với k chẵn, đạt cực đại tại \(x = k.{\pi \over 2}\) với k lẻ, và
\({y_{CT}} = y(2m\pi ) = 0;\)
\({y_{CĐ}} = y((2m + 1){\pi \over 2}) = 1(m \in Z)\)
Bài 1.15 trang 15 Sách bài tập (SBT) Giải tích 12
Xác định giá trị của m để hàm số sau có cực trị:
a) \(y = {x^3} - 3{x^2} + mx - 5\)
b) \(y = {x^3} + 2m{x^2} + mx - 1\)
c) \(y = {{{x^2} - 2mx + 5} \over {x - m}}\)
Hướng dẫn làm bài:
a) TXĐ: D = R
\(y' = 3{x^2} - 6x + m\)
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.
⇔ 3x2 – 6x + m có hai nghiệm phân biệt.
⇔ ∆’ = 9 – 3m > 0 ⇔ 3m < 9 ⇔ m < 3.
Vậy hàm số đã cho có cực trị khi m < 3.
b) TXĐ: D = R
y’ = 3x2 + 4mx + m
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên R.
⇔ 3x2 + 4mx + m có hai nghiệm phân biệt.
⇔ ∆’ = 4m2 -3m > 0 ó m(4m – 3) > 0
\(\Leftrightarrow \left[ \matrix{
m < 0 \hfill \cr
m > {3 \over 4} \hfill \cr} \right.\)
Vậy hàm số đã cho có cực đại, cực tiểu khi m < 0 hoặc \(m > {3 \over 4}\).
c) TXĐ: D = R\{m}
\(y' = {{{x^2} - 2mx + 2{m^2} - 5} \over {{{(x - m)}^2}}}\)
Hàm số có cực trị khi và chỉ khi y’ đổi dấu trên D
⇔ x2 – 2mx + 2m2 – 5 có hai nghiệm phân biệt.
⇔ ∆’ = - m2 + 5 > 0 ⇔ \(- \sqrt 5 < m < \sqrt 5\)
Bài 1.16 trang 15 Sách bài tập (SBT) Giải tích 12
Xác định giá trị của tham số m để hàm số y = x3 – 2x2 + mx + 1 đạt cực tiểu tại x = 1.
Hướng dẫn làm bài:
TXĐ: D = R
y’ = 3x2 – 4x + m ; y’ = 0 ⇔ 3x2 – 4x + m = 0
Phương trình trên có hai nghiệm phân biệt khi:
∆’ = 4 – 3m > 0 ⇔ m<\(\frac{4}{3}\)(*)
Hàm số có cực trị tại x = 1 thì:
y’(1) = 3 – 4 + m = 0 => m = 1 (thỏa mãn điều kiện (*))
Mặt khác, vì:
y’’ = 6x – 4 => y’’(1) = 6 – 4 = 2 > 0
cho nên tại x = 1, hàm số đạt cực tiểu.
Vậy với m = 1, hàm số đã cho đạt cực tiểu tại x = 1
Bài 1.17 trang 16 Sách bài tập (SBT) Giải tích 12
Xác định m để hàm số: \(y = {x^3} - m{x^2} + (m - {2 \over 3})x + 5\) có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Hướng dẫn làm bài:
\(y = {x^3} - m{x^2} + (m - {2 \over 3})x + 5\)
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có:
\(y' = 3{x^2} - 2mx + (m - {2 \over 3})\)
∆’ > 0 khi m < 1 hoặc m > 2 (*)
Để hàm số có cực trị tại x = 1 thì
\(y'(1) = 3 - 2m + m - {2 \over 3} = 0 < = > m = {7 \over 3}\), thỏa mãn điều kiện (*)
Với \(m = {7 \over 3}\) thì hàm số đã cho trở thành:
\(y = {x^3} - {7 \over 3}{x^2} + {5 \over 3}x + 5\)
Ta có:
\(y' = 3{x^2} - {{14} \over 3}x + {5 \over 3}\)\(y'' = 6x - {{14} \over 3}\)
Vì \(y''(1) = 6 - {{14} \over 3} > 0\) nên hàm số đạt cực tiểu tại x = 1 và \({y_{CT}} = {y_{\left( 1 \right)}} = {{16} \over 3}\)
Bài 1.18 trang 16 Sách bài tập (SBT) Giải tích 12
Chứng minh rằng hàm số:
\(f(x) = \left\{ \matrix{
- 2x,\forall x \ge 0 \hfill \cr
\sin {x \over 2},\forall x < 0 \hfill \cr} \right.\)
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.
Hướng dẫn làm bài:
Hàm số:
\(f(x) = \left\{ \matrix{
- 2x,\forall x \ge 0 \hfill \cr
\sin {x \over 2},\forall x < 0 \hfill \cr} \right.\)
Không có đạo hàm tại x = 0 vì:
\(\mathop {\lim }\limits_{x \to {0^ + }} {{f(x) - f(0)} \over x} = \mathop {\lim }\limits_{x \to {0^ + }} {{ - 2x} \over x} = - 2\)\(\mathop {\lim }\limits_{x \to {0^ + }} {{f(x) - f(0)} \over x} = \mathop {\lim }\limits_{x \to {0^ + }} {{ - 2x} \over x} = - 2\)
Mặt khác, với x < 0 thì \(y' = {1 \over 2}\cos {x \over 2}\), với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
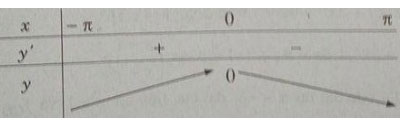
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và yCĐ = y(0) = 0.
Bài 1.19 trang 16 Sách bài tập (SBT) Giải tích 12
Xác định giá trị m để hàm số sau không có cực trị.
y=x2+2mx−3x−m
Hướng dẫn làm bài:
Hàm số không có cực trị khi đạo hàm của nó không đổi dấu trên tập xác định R\{m}.
Ta có:
\(y = {{{x^2} + 2mx - 3} \over {x - m}}\)\(y' = {{(2x + 2m)(x - m) - ({x^2} + 2mx - 3)} \over {{{(x - m)}^2}}}\)\(= {{2{x^2} - 2{m^2} - {x^2} - 2mx + 3} \over {{{(x - m)}^2}}} = {{{x^2} - 2mx - 2{m^2} + 3} \over {{{(x - m)}^2}}}\)
Xét g(x) = x2 – 2mx – 2m2 + 3
∆’g = m2 + 2m2 – 3 = 3(m2 – 1);
∆’g ≤ 0 khi – 1 ≤ m ≤ 1.
Khi – 1 ≤ m ≤ 1 thì phương trình g(x) = 0 vô nghiệm hay y’ = 0 vô nghiệm và y’ > 0 trên tập xác định. Khi đó, hàm số không có cực trị.
Khi m = 1 hoặc m = -1, hàm số đã cho trở thành y = x + 3 (với x ≠ 1) hoặc y = x – 3 (với x ≠ - 1) Các hàm số này không có cực trị.
Vậy hàm số đã cho không có cực trị khi – 1 ≤ m ≤ 1.
