Giải vở bài tập Đại số lớp 12 bài 1: Sự đồng biến, nghịch biến của hàm số
Giải vở bài tập Đại số lớp 12 bài 1 chương 1
VnDoc.com xin giới thiệu tới bạn đọc tài liệu: Giải vở bài tập Đại số lớp 12 bài 1: Sự đồng biến, nghịch biến của hàm số, với cách giải bài tập Toán 12 một cách chi tiết sẽ giúp các bạn học sinh học tốt Toán lớp 12 và có kết quả cao hơn trong học tập. VnDoc.com mời các bạn học sinh và thầy cô tham khảo.
Đề kiểm tra 15 phút môn Toán 12: Sự đồng biến, nghịch biến của hàm số
Lý thuyết Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
Trắc nghiệm Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
Giải vở bài tập Đại số lớp 12 bài 1: Sự đồng biến, nghịch biến của hàm số
Bài 1.1 trang 7 Sách bài tập (SBT) Giải tích 12
Xét sự đồng biến, nghịch biến của các hàm số:
a) 
\(y = 3{x^2} - 8{x^3}\)
b) \(y = 16x + 2{x^2} - {{16} \over 3}{x^3} - {x^4}\)
c) \(y = {x^3} - 6{x^2} + 9x\)
d) \(y = {x^4} + 8{x^2} + 5\)
Hướng dẫn làm bài
a) TXĐ: R
\(y' = 6x - 24{x^2} = 6x(1 - 4x)\)
\(y' = 0 <=> \left[ {\matrix{{x = 0} \cr {x = {1 \over 4}} \cr} } \right.\)
y' > 0 trên khoảng \((0;{1 \over 4})\) , suy ra y đồng biến trên khoảng \((0;({1 \over 4})\)
y' < 0 trên các khoảng \((-∞;0 ); ({1 \over 4}; + \infty )\) suy ra y nghịch biến trên các khoảng \((-∞;0 ); ({1 \over 4}; + \infty )\)
b) TXĐ: R
\(y' = 16 + 4x - 16{x^2} - 4{x^3} = - 4(x + 4)({x^2} - 1)\)
\(y' = 0 <=> \left[ {\matrix{{x = - 4} \cr {x = - 1} \cr {x = 1} \cr} } \right.\)
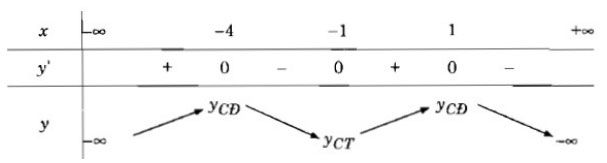
Vậy hàm số y đã cho đồng biến trên các khoảng \((-∞; -4)\)\(và (-1; 1)\), nghịch biến trên các khoảng (-4; -1) và \((1; +∞)\)
c) TXĐ: R
\(y' = 3{x^2} - 12x + 9\)
\(y'=0 <=> \left[ {\matrix{{x = 1} \cr {x = 3} \cr} } \right.\)
y' > 0 trên các khoảng \((-∞; 1), (3; +∞)\) nên y đồng biến trên các khoảng \((-∞; 1), (3; +∞)\)
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
\(y'=4x^3+16x=4x(x^2+4)\)
y' = 0 <=> x = 0
y' > 0 trên khoảng \((0; +∞)\) => y đồng biến trên khoảng \((0; +∞)\)
y' < 0 trên khoảng \((-∞; 0)\)=> y nghịch biến trên khoảng \((-∞; 0)\)
Bài 1.2 trang 7 Sách bài tập (SBT) Giải tích 12
a) \(y = {{3 - 2x} \over {x + 7}}\)
b) \(y = {1 \over {{{(x - 5)}^2}}}\)
c) \(y = {{2x} \over {{x^2} - 9}}\)
d) \(y = {{{x^4} + 48} \over x}\)
e) \(y = {{{x^2} - 2x + 3} \over {x + 1}}\)
g) \(y = {{{x^2} - 5x + 3} \over {x - 2}}\)
Hướng dẫn làm bài
a) TXĐ: R\ {-7}
\(y' = {{ - 17} \over {{{(x + 7)}^2}}}\)
y' < 0 trên các khoảng \((-∞; -7), (-7; +∞)\) nên hàm số nghịch biến trên các khoảng đó
b) TXĐ: R\ {5}
\(y' = {{ - 2} \over {{{(x - 5)}^3}}}\)
y' < 0 trên khoảng \((5; +∞)\) nên y nghịch biến trên khoảng \((5; +∞)\)
y' > 0 trên khoảng \((-∞; 5)\) nên y đồng biến trên khoảng \((-∞; 5)\)
c) TXĐ: R\{-3; 3}
\(y' = {{ - 2({x^2} + 9)} \over {{{({x^2} - 9)}^2}}}\)
y' < 0 trên các khoảng \((-∞; - 3), (-3; 3), (3; +∞)\) nên hàm số đã cho nghịch biến trên các khoảng đó.
d) TXĐ: R\ {0}
\(y' = {{3({x^4} - 16)} \over {{x^2}}} = {{3({x^2} - 4)({x^2} + 4)} \over {{x^2}}}\)
\(y' = 0 <=> \left[ {\matrix{{x = - 2} \cr {x = 2} \cr} } \right.\)
Bảng biến thiên
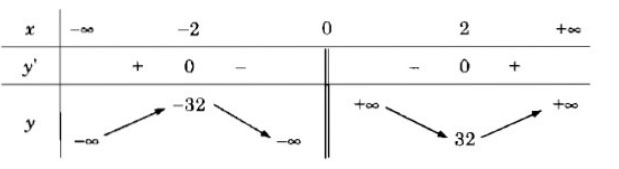
Vậy hàm số đã cho đồng biến trên các khoảng \((-∞; -2), (2; +∞)\) và nghịch biến trên các khoảng (-2; 0), (0; 2)
e) TXĐ: R \ {-1}
\(y' = {{{x^2} + 2x - 5} \over {{{(x + 1)}^2}}}\)
\(y' = 0 <=> \left[ {\matrix{{x = - 1 - \sqrt 6 } \cr {x = - 1 + \sqrt 6 } \cr} } \right.\)
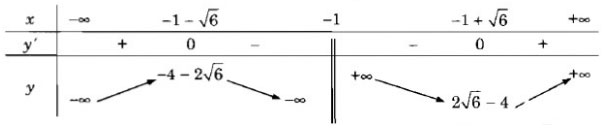
Vậy hàm số đã cho đồng biến trên các khoảng \(( - \infty ; - 1 - \sqrt 6 ),( - 1 + \sqrt 6 ; + \infty )\)
và nghịch biến trên các khoảng \(( - 1 - \sqrt 6 ; - 1),( - 1; - 1 + \sqrt 6 )\)
g) TXĐ: R\ {2}
\(y' = {{{x^2} - 4x + 7} \over {{{(x - 2)}^2}}} > 0\)
(do \({x^2} - 4x + 7\) có ∆' = - 3 < 0)
Vậy hàm số đã cho đồng biến trên các khoảng \(( - \infty ;2),(2; + \infty )\)
Bài 1.3 trang 8 Sách bài tập (SBT) Giải tích 12
a) \(y = \sqrt {25 - {x^2}}\)
b) \(y = {{\sqrt x } \over {x + 100}}\)
c) \(y = {x \over {\sqrt {16 - {x^2}} }}\)
d) \(y = {{{x^3}} \over {\sqrt {{x^2} - 6} }}\)
Hướng dẫn làm bài
a) TXĐ: [-5; 5]
\(y' = {{ - x} \over {\sqrt {25 - {x^2}} }}\) \(; y’ = 0 <=> x = 0\)
Bảng biến thiên
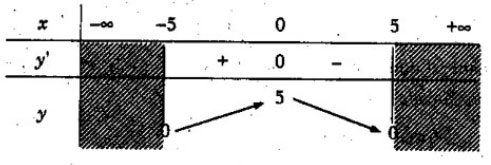
Vậy hàm số đồng biến trên khoảng (-5; 0) nghịch biến trên khoảng (0; 5)
b) TXĐ: \([0; +∞)\)
\(y' = {{100 - x} \over {2\sqrt x {{(x + 100)}^2}}}\)\(; y’ = 0 <=> x = 100\)
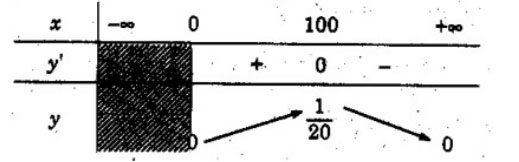
Vậy hàm số đồng biến trên khoảng (0; 100) và nghịch biến trên khoảng \((100; +∞)\)
c) TXĐ: (-4; 4)
\(y' = {{16} \over {(16 - {x^2})\sqrt {16 - {x^2}} }}\)> 0 ; ∀ x ∈ (-4; 4)
Vậy hàm số đồng biến trên khoảng (-4; 4).
d) TXĐ:\((-∞; √66) ∪ (√66; +∞)\)
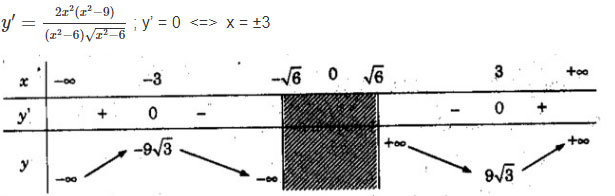
Vậy hàm số đồng biến trên các khoảng \((-∞; -3), (3; +∞)\), nghịch biến trên các khoảng \((-3;-\sqrt 6 ), (\sqrt 6 ; 3)\).
Bài 1.4 Trang 8 Sách bài tập (SBT) Giải tích 12
Xét sự đồng biến, nghịch biến của các hàm số:
a) \(y = x - {\mathop{\rm s}\nolimits} {\rm{inx}}, x ∈ [0; 2π].\)
b) \(y = x + 2\cos x , x ∈ ({\pi \over 6};{{5\pi } \over 6})\)
c) \(y = \sin {1 \over x} , (x > 0)\)
Hướng dẫn làm bài
a) \(y = x - {\mathop{\rm s}\nolimits} {\rm{inx}}, x ∈ [0; 2π].\)
\(y' = 1 - c{\rm{osx }} ≥ 0\) với mọi x ∈ [0; 2π]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.
Vậy hàm số đồng biến trên đoạn [0; 2π].
b) \(y = x + 2\cos x , x ∈ ({\pi \over 6};{{5\pi } \over 6})\)
\(y' = 1 - 2\sin x\) < 0 với \(x ∈\) \(({\pi \over 6};{{5\pi } \over 6})\)
Do đó, hàm số nghịch biến trên khoảng \(({\pi \over 6};{{5\pi } \over 6})\)
c) Xét hàm số \(y = \sin {1 \over x}\) với x > 0.
\(y' = - {1 \over {{x^2}}}\cos {1 \over x}\)
Giải bất phương trình sau trên khoảng \((0; +∞)\)
\({1 \over {{x^2}}}( - \cos {1 \over x}) > 0 ⟺ \cos {1 \over x}) < 0\)
⟺ \({\pi \over 2}(1 + 4k) < {1 \over x} < {\pi \over 2}(3 + 4k) ,k = 0, 1, 2 ….\)
⟺ \({2 \over {\pi (1 + 4k)}} > x > {2 \over {\pi (3 + 4k)}} , k = 0, 1, 2 ……..\)
Do đó, hàm số đồng biến trên các khoảng
\(....,({2 \over {(4k + 3)\pi }};{2 \over {(4k + 1)\pi }}),({2 \over {(4k - 1)\pi }};{2 \over {(4k - 3)\pi }}),.....,\)\(({2 \over {7\pi }};{2 \over {5\pi }}),({2 \over {3\pi }};{2 \over \pi })\)
Và nghịch biến trên các khoảng
\(……, ({2 \over {(4k + 1)\pi }};{2 \over {(4k - 1)\pi }}),({2 \over {5\pi }};{2 \over {3\pi }}),.....,\)\(({2 \over \pi }; + \infty )\)
với k = 0, 1, 2 …
Bài 1.5 trang 8 Sách bài tập (SBT) Giải tích 12
Xác định m để hàm số sau:
a) \(y = {{mx - 4} \over {x - m}}\) đồng biến trên từng khoảng xác định;
b) \(y = {{ - mx - 5m + 4} \over {x + m}}\) nghịch biến trên từng khoảng xác định;
c) \(y = - {x^3} + m{x^2} - 3x + 4\) nghịch biến trên;
d) \(y = {x^3} - 2m{x^2} + 12x - 7\) đồng biến trên R.
Hướng dẫn làm bài:
a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng \(( - \infty ;m),(m; + \infty )\) khi và chỉ khi:
\(y' = {{ - {m^2} + 4} \over {{{(x - m)}^2}}} > 0 \Leftrightarrow - {m^2} + 4 > 0\)\({m^2} < 4 \Leftrightarrow - 2 < m < 2\)
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
\(y' = {{ - {m^2} + 5m - 4} \over {{{(x + m)}^2}}} < 0 \Leftrightarrow - {m^2} + 5m-4 < 0\)
\(\left[ \matrix{
m < 1 \hfill \cr
m > 4 \hfill \cr} \right.\)
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
\(y' = - 3{x^2} + 2mx - 3 \le 0 \Leftrightarrow ' = {m^2} - 9 \le 0 \Leftrightarrow {m^2} \le 9\)
⇔ \(- 3 \le m \le 3\)
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
\(y' = 3{x^2} - 4mx + 12 \ge 0 \Leftrightarrow ' = 4{m^2} - 36 \le 0\)
⇔ \({m^2} \le 9 \Leftrightarrow - 3 \le m \le 3\)
Bài 1.6 trang 8 Sách bài tập (SBT) Giải tích 12
Chứng minh các phương trình sau có nghiệm duy nhất
a) \(3(c{\rm{os x - 1) + }}{\rm{2sin x + 6x = 0}}\)
b) \(4x + c{\rm{os x - 2sin x - 2 = 0}}\)
c) \(- {x^3} + {x^2} - 3x + 2 = 0\)
d) \({x^5} + {x^3} - 7 = 0\)
Hướng dẫn làm bài
a) Đặt y = 3(cos x – 1) + 2sin x + 6
Hàm số xác định, liên tục và có đạo hàm tại mọi x ∈ R
Ta có: y( ) = 0 và ý = -3sin x + 2cos x + 6 >0, x ∈ R.
Hàm số đồng biến trên R và có một nghiệm \(x = \pi\)
Vậy phương trình đã cho có một nghiệm duy nhất.
b) Đặt \(y = 4x + \cos x - 2\sin x - 2\)
Hàm số xác định, liên tục và có đạo hàm tại mọi x ∈ R
Ta có: y(0) = 1 – 2 = -1 < 0 ; \(y(\pi ) = 4 .\)
Hàm số liên tục trên \({\rm{[}}0;\pi {\rm{]}}\) và y’(0) < 0 nên tồn tại \({x_0} \in (0;\pi )\) sao cho \(y({x_0}) = 0\)
Suy ra phương trình có một nghiệm \({x_0}\)
c) Đặt y = – x3 + x2 – 3x + 2
Hàm số xác định, liên tục và có đạo hàm trên R.
Ta có: y’ = – x2 + 2x – 3 < 0, \(y(\pi ) = 4\pi - 3 > 0, x ∈ R.\)
Vì a = -3 < 0 và . Suy ra y nghịch biến trên R.
Mặt khác y(-1) = 1 + 1 +3 + 2 = 7 > 0
y(1) = -1 +1 – 3 + 2 = -1 < 0
Hàm số liên tục trên [-1; 1] và y(-1)y(1) < 0 cho nên tồn tại \({x_0} \in {\rm{[}} - 1;1]\) sao cho \(y({x_0}) = 0\)
Suy ra phương trình đã cho có đúng một nghiệm.
d) Đặt y = x5 + x3 – 7
Hàm số xác định, liên tục và có đạo hàm trên R.
Ta có: y(0) = -7 < 0 ; y(2) = 32 + 8 – 7 = 33 > 0
Hàm số liên tục trên [0; 2] và y(0) y(2) < 0 cho nên tồn tại \({x_0} \in (0;2)\) sao cho \(y({x_0}) = 0\)
Mặt khác \(y' = 5{x^4} + 3{x^2} = {x^2}(5{x^2} + 3) \ge 0,\forall x \in R\)
=> Hàm số đồng biến trên \(( - \infty ; + \infty )\)
Suy ra phương trình đã cho có đúng một nghiệm.
Bài 1.7 trang 8 Sách bài tập (SBT) Giải tích 12
Chứng minh phương trình \({x^5} - {x^2} - 2x - 1 = 0\) có nghiệm duy nhất
(Đề thi đại học năm 2004)
Hướng dẫn làm bài:
Trước hết cần tìm điều kiện của nghiệm phương trình (tức là xem nghiệm phương trình, nếu có, phải nằm trong khoảng nào). Ta nhận xét
x5 – x2 – 2x – 1 = 0 ⇔ x5 = (x + 1)2 0 => x ≥ 0
=> (x + 1)2 1 => x5 1 => x 1
Vậy, nếu có, nghiệm của phương trình phải thuộc \({\rm{[}}1; + \infty {\rm{]}}) .\)
Xét hàm số \(f(x) = {x^5} - {x^2} - 2x - 1\)ta thấy f(x) liên tục trên R
Mặt khác, \(f(1) = - 3 < 0,f(2) = 23 > 0\)
Vì f(x) liên tục trên [1; 2] và f(1) f(2) < 0 nên tồn tại \({x_0} \in (1;2)\) sao cho \(f({x_0}) = 0\)
Ta có: f’(x) = 5x4 – 2x – 2 = (2x4 – 2x) + (2x4 – 2) + x4
= 2x(x3 – 1) + 2(x4 – 1) + x4 > 0 , \(\forall x \ge 1\)
Suy ra f(x) đồng biến trên \({\rm{[}}1; + \infty {\rm{]}}\)
Bài 1.8 trang 8 Sách bài tập (SBT) Giải tích 12
Chứng minh các bất đẳng thức sau:
a) \(\tan x > \sin x,0 < x < {\pi \over 2}\)
b) \(1 + {1 \over 2}x - {{{x^2}} \over 8} < \sqrt {1 + x} < 1 + {1 \over 2}x\) với \(0 < x < + \infty\)
Hướng dẫn làm bài:
a) Xét hàm số \(f(x) = \tan x - \sin x\) trên nửa khoảng \({\rm{[}}0;{\pi \over 2})\);
\(f'(x) = {1 \over {{{\cos }^2}x}} - \cos x = {{1 - {{\cos }^3}x} \over {{{\cos }^2}}} \ge 0;x \in {\rm{[}}0;{1 \over 2})\)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng \({\rm{[}}0;{\pi \over 2})\)
Mặt khác, ta có f(0) = 0, nên f(x) = tan x – sin x > 0 hay tan x > sin x với mọi \(x \in {\rm{[}}0;{1 \over 2})\)
b) Xét hàm số \(h(x) = 1 + {1 \over 2}x - \sqrt {1 + x}\) trên \({\rm{[}}0; + \infty )\)
\(h'(x) = {1 \over 2} - {1 \over {2\sqrt {1 + x} }} \ge 0\)\(1 + {1 \over 2}x - {{{x^2}} \over 8} < \sqrt {1 + x} ,0 \le x \le + \infty\)
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng \({\rm{[}}0; + \infty )\).
Vì h(x) = 0 nên \(h(x) = 1 + {1 \over 2}x - \sqrt {1 + x} > 0\)
Hay \(1 + {1 \over 2}x > \sqrt {1 + x}\) với \(0 \le x < + \infty\)
Xét hàm số trên \(f(x) = \sqrt {1 + x} - 1 - {1 \over 2}x + {{{x^2}} \over 8}\)trên \({\rm{[}}0; + \infty ) ;\)
\(g(x) = f'(x) = {1 \over {2\sqrt {1 + x} }} - {1 \over 2} + {x \over 4}\)
\(g'(x) = {1 \over 4} - {1 \over {4(1 + x)\sqrt {1 + x} }} \ge 0,0 \le x < + \infty\)
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng \({\rm{[}}0; + \infty )\) nên \(g(x) \ge 0\), tức là \(f'(x) \ge 0\) trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng.
Mặt khác, ta có f(0) = 0 nên
\(f(x) = \sqrt {1 + x} - 1 - {1 \over 2}x + {{{x^2}} \over 8} > 0\)
hay \(1 + {1 \over 2}x - {{{x^2}} \over 8} < \sqrt {1 + x}\)
Với mọi \(0 < x < + \infty\).
Bài 1.9 trang 9 Sách bài tập (SBT) Giải tích 12
Chứng minh rằng phương trình \({x^3} - 3x + c = 0\) không thể có hai nghiệm thực trong đoạn [0; 1].
Hướng dẫn làm bài:
Đặt \(f(x) = {x^3} - 3x + c\). TXĐ: R
\(f'(x) = 3{x^2} - 3 = 3({x^2} - 1)\)
\(f'(x) = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = - 1 \hfill \cr} \right.\)
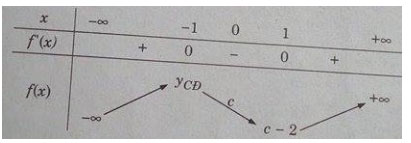
Trên đoạn [0; 1] hàm số f(x) nghịch biến nên đồ thị của hàm số f(x) không thể cắt trục hoành tại hai điểm trên đoạn này, tứclà phương trình \({x^3} - 3x + c = 0\) không thể có hai nghiệm thực trên đoạn [0; 1].
Bài 1.10 trang 9 Sách bài tập (SBT) Giải tích 12
Xác định giá trị của b để hàm số \(f(x) = \sin x - bx + c\) nghịch biến trên toàn trục số.
Hướng dẫn làm bài:
\(f(x) = \sin x - bx + c\) nghịch biến trên R nếu ta có:
\(f'(x) = \cos x - b \le 0,\forall x \in R\)
Vì \(|\cos x| \le 1\) nên \((f'(x) \le 0,\forall x \in R < = > b \ge 1.\)
