Giải SBT Toán 12: Câu hỏi trắc nghiệm ôn tập cuối năm
Hình học 12: Câu hỏi trắc nghiệm ôn tập cuối năm
VnDoc xin giới thiệu tới bạn đọc Giải SBT Toán 12: Câu hỏi trắc nghiệm ôn tập cuối năm. Tài liệu kèm theo lời giải chi tiết sẽ giúp các bạn giải bài tập Toán 12 hiệu quả hơn. Mời các bạn học sinh tham khảo.
Bài tập trắc nghiệm trang 170, 171, 172, 173, 174 Sách bài tập Hình học 12:
Bài 1: Cho hình chóp ngũ giác S.ABCDE. Gọi A', B', C', D', E' lần lượt là trung điểm của SA, SB, SC, SD, SE. Khi đó:
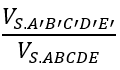
A. 1/2
B. 1/5
C. 1/8
D. 1/32
Bài 2: Thể tích hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a bằng:
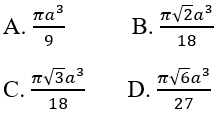
Bài 3: Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khi đó thể tích hình chóp A.A'BCD' bằng:
A. a3/2
B. a3/3
C. a3/4
D. a3/6
Bài 4: Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó:
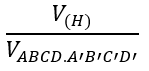
A. 1/3
B. π/6
C. π/8
D. π/12
Bài 5: Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình trụ tròn xoay ngoại tiếp hình lập phương đó. Khi đó:
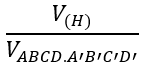
A. 3/2
B. π/2
C. π/3
D. π/(√3)
Bài 6: Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình cầu nội tiếp hình lập phương đó. Khi đó:
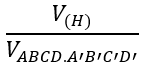
A. π/6
B. π/4
C. π/3
D. π/(√3)
Bài 7: Cho một mặt cầu có diện tích S, thể tích khối cầu đó là V. Bán kính R của mặt cầu là:
A. R = 4V/S
B. R = S/3V
C. R = 3V/S
D. R = V/3S
Bài 8: Cho mặt cầu S(O;R) và điểm A cố định với OA = d > R. Qua A kẻ đường thẳng Δ tiếp xúc với mặt cầu S(O;R) tại M. Độ dài đoạn thẳng AM là:
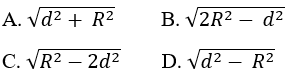
Bài 9: Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật. Tâm của mặt cầu (S) là:
A. Tâm của hình hộp chữ nhật
B. Tâm của một mặt bên của hình hộp chữ nhật
C. Trung điểm của một cạnh của hình hộp chữ nhật
D. Một đỉnh bất kì của hình hộp chữ nhật
Bài 10: Cho mặt cầu S(O;R) và đường thẳng Δ. Biết khoảng cách từ O tới Δ bằng d. Với điều kiện nào sau đây thì đường thẳng Δ tiếp xúc với mặt cầu S(O;R)?
A. d = R
B. d > R
C. d < R
D. d ≠ R
Bài 11: Cho đường tròn (C) và điểm A nằm ngoài mặt phẳng chứa (C). Có tất cả bao nhiêu mặt cầu chứa đường tròn (C) và đi qua A?
A. 0
B. 1
C. 2
D. Vô số
Bài 12: Cho hai điểm A, B phân biệt. Tập hợp tâm những mặt cầu đi qua A và B là
A. Mặt phẳng trung trực của đoạn thẳng AB
B. Đường trung trực của AB
C. Mặt phẳng song song với đường thẳng AB
D. Trung điểm của đoạn AB
Bài 13: Từ điểm M nằm ngoài mặt cầu S(O;R) có thể kẻ được bao nhiêu tiếp tuyến với mặt cầu?
A. 0
B. 1
C. 2
D. Vô số
Bài 14: Một đường thẳng d thay đổi qua A và tiếp xúc với mặt cầu S(O;R) tại M. Gọi H là hình chiếu của M lên đường thẳng OA. M thuộc mặt phẳng nào trong những mặt phẳng sau đây?
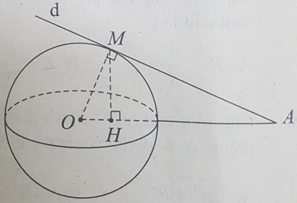
A. Mặt phẳng qua H và vuông góc với OA
B. Mặt phẳng trung trực của OA
C. Mặt phẳng qua O và vuông góc với AM
D. Mặt phẳng qua A và vuông góc với OM.
Bài 15: Một khinh khí cầu có một mặt cầu có đường kính 11m. Nếu làm tròn kết quả đến chữ số thập phân thứ hai, thì diện tích bề mặt khinh khí cầu là:
A. 379,94 (m2)
B. 697,19 (m2)
C. 190,14 (m2)
D. 95,07 (m2)
Bài 16: Cho hình nón có thiết diện qua trục là một tam giác đều cạnh 2a và thể tích là V1 và hình cầu có đường kính bằng chiều cao hình nón, có thể tích là V2.
Tỉ số thể tích V1/V2 là:
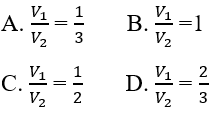
Bài 17: Diện tích xung quanh của hình trụ có bán kính đáy a và đường cao a√3 là:
A. 2πa2√3
B. 2πa2
C. πa2
D. πa2√3
Bài 18: Một hình nón có đường kính đáy là 2aπ3, góc ở đỉnh 120o. Thể tích của khối nón đó theo a là:
A. 2√3πa3
B. 3πa3
C. πa3
D. πa3√3
Bài 19: Cho một hình trụ có bán kính đáy R, chiều cao h, thể tích V1 và một hình nón có đáy trùng với đáy của một hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (xem hình) và thể tích V2. Hệ thức giữa V1 và V2 là:
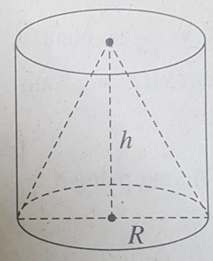
A. V1 = 2V2
B. V1 = 3V2
C. V2 = 3V1
D. V2 = V1
Bài 20: Một khối trụ có chu vi đáy bằng 6π cm và thiết diện đi qua là một hình chữ nhật có độ dài đường chéo bằng 10 cm. Thể tích khối trụ là:
A. 72π (cm3)
B. 24π (cm3)
C. 48π (cm3)
D. 18π√(34) (cm3)
Các bài tập dưới đây cho trong không gian Oxyz
Bài 21: Cho A(0; 0; a), B(b; 0; 0), C(0; c; 0). Phương trình mặt phẳng (ABC) là:
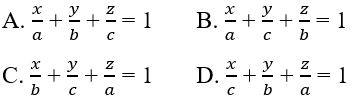
Bài 22: Cho ba mặt phẳng:
(P): 2x + y + z + 3 = 0
(Q): x - y - z - 1 = 0
(R): y - z + 2 = 0
Khẳng định nào sau đây là sai?
A. Không có điểm nào cùng thuộc ba mặt phẳng trên
B. (P) ⊥ (Q)
C. (P) ⊥ (R)
D. (Q) ⊥ (R)
Bài 23: Cho hai đường thẳng
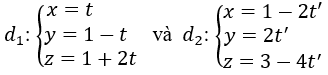
Khẳng định nào sau đây là đúng?
A. d1 và d2 cắt nhau
B. d1 và d2 chéo nhau
C. d1 và d2 song song
D. d1 và d2 trùng nhau
Bài 24: Cho đường thẳng
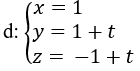
và hai mặt phẳng: (P): x - y + z + 1 = 0 và (Q): 2x + y - z - 4 = 0
Khẳng định nào sau đây là đúng?
A. d // (P)
B. d // (Q)
C. d = (P) ∩ (Q)
D. d ⊥ (P).
Đáp án và hướng dẫn giải
| 1. C | 2. D | 3. B | 4. D | 5. B | 6. A |
| 7. C | 8. D | 9. A | 10. A | 11. B | 12. A |
| 13. D | 14. A | 15. A | 16. D | 17. A | 18. C |
| 19. B | 20. A | 21. C | 22. A | 23. D | 24. C |
Bài 1: Chọn C.
Bài 2: Chọn D.
Hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a có bán kính đáy r = a√3/3 và có chiều cao và chiều cao tứ diện đều và bằng a√6/3
Thể tích hình nón là:
![]()
Bài 3: Chọn B.
Hình nón A.A'BCD' với đáy là hình chữ nhật A'BCD' có diện tích S = A'B.BC = a2√2 và chiều cao h = (a√2)/2 nên có thể tích V = a3/3
Bài 4: Chọn D.
Gọi 2a là cạnh của hình lập phương ta có hình nón tròn xoay nội tiếp hình lập phương đó có bán kính đáy r = a và chiều cao h = 2a
Suy ra:
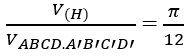
Bài 5: Chọn B
Gọi a là cạnh của hình lập phương ta có hình trụ tròn xoay ngoại tiếp hình lập phương đó có bán kính đáy r = (a√2)/2 và chiều cao h = a.
Suy ra:
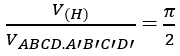
Bài 6: Chọn A.
Gọi 2a là cạnh của hình lập phương thì hình cầu nội tiếp hình lập phương đó có bán kính r = a.
Suy ra:
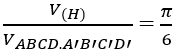
Bài 7: Chọn C.
Dựa vào công thức diện tích mặt cầu và thể tích hình cầu, ta có:
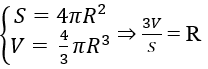
Bài 8: Chọn D.
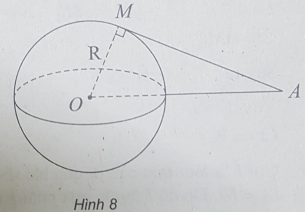
(h.8) Vì Δ tiếp xúc với S(O;R) tại M nên OM ⊥ Δ tại M.
Xét tam giác OMA vuông tại M, ta có:
AM2 = OA2 - OM2 = d2 - R2
![]()
Bài 9: Chọn A.
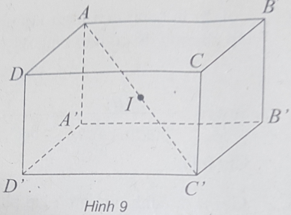
(h.9) Tâm của hình hộp chữ nhật cách đều 8 đỉnh của hình hộp nên tâm của mặt cầu (S) chính là tâm của hình hộp chữ nhật.
Bài 10: Chọn A.
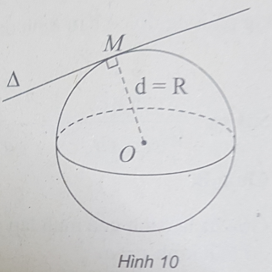
(h.10) Đường thẳng Δ tiếp xúc với mặt cầu S(O;R) khi d = R.
Bài 11: Chọn B.
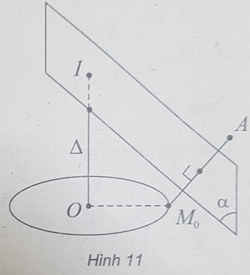
(h.11) Lấy điểm M0 cố định trên đường tròn (C).
Gọi (α) là mặt phẳng trung trực của AM0 và đường thẳng Δ là trục của (C)
Ta có: I = (α) ∩ Δ là tâm mặt cầu thỏa mãn yêu cầu đề bài.
Nhận xét: Tâm I là duy nhất. Thật vậy, giả sử M nằm trên đường tròn (C) khác với M0
Gọi (α') là mặt phẳng trung trực của AM và I' = (α') ∩ Δ
Khi đó, mặt cầu tâm I' thỏa mãn yêu cầu đề bài.
Ta có: I'A = I'M = I'M0 cho ta I' thuộc mặt phẳng trung trực (α) của AM0
Suy ra: I' = (α) ∩ Δ
Vậy I' ≡ I
Bài 12: Chọn A.
Gọi I là tâm mặt cầu đi qua hai điểm A, B cố định và phân biệt thì ta luôn có IA = IB. Do đó I thuộc mặt phẳng trung trực của đoạn AB.
Bài 13: Chọn D.
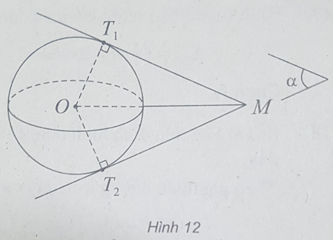
(h.12) Gọi (α) là mặt phẳng chứa đường thẳng MO
Ta có: (α) cắt mặt cầu S(O;R) theo giao tuyến là đường tròn (C) có tâm O, bán kính R.
Trong mặt phẳng (α), từ điểm M nằm ngoài (C) ta luôn kẻ được hai tiếp tuyến MT1, MT2 với đường tròn (C). Đây cũng là hai tiếp tuyến với mặt cầu S(O;R).
Nhận xét: Do có vô số mặt phẳng (α) chứa đường thẳng MO. Những mặt phẳng này cắt mặt cầu S(O;R) theo các giao tuyến là đường tròn khác nhau nên cũng có vô số tiếp tuyến với mặt cầu được kẻ từ điểm M nằm ngoài mặt cầu.
Bài 14: Chọn A.
Trong mặt phẳng (d,O), tam giác OMA vuông tại M có MH là đường cao nên:
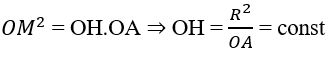
⇒ H cố định
Vậy M thuộc mặt phẳng vuông góc với OA tại H.
Bài 15: Chọn A.
Diện tích của khing khí cầu là: S = πd2 = 379,94 (m2)
Bài 16: Chọn D.
Hình nón có bán kính đáy là a, chiều cao a√3 nên có thể tích:
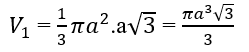
Hình cầu có bán kính (a√3)/2 nên có thể tích:
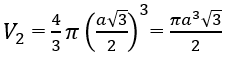
Từ đó suy ra:
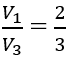
Bài 17: Chọn A.
Hình trụ có bán kính đáy a và đường cao a√3 nên:
Sxq = 2πrh = 2πa.a√3 = 2πa2√3
Bài 18: Chọn C.
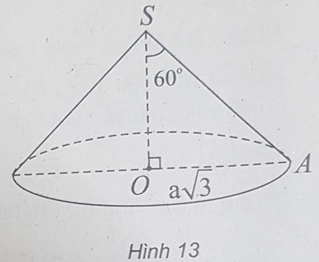
(h.13) Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Theo giả thiết, đường tròn đáy có bán kính R = OA = a√3 và ∠ = 60o0
Trong tam giác SOA vuông tại O, ta có: OA = SO.tan60o ⇒ SO = a.
Do đó chiều cao của hình nón là h = a.
Vậy thể tích hình nón là: V = πa3
Bài 19: Chọn B.
Hình trụ có bán kính đáy R và chiều cao h nên thể tích V1 = πR2h.
Hình nón có bán kính đáy R và chiều cao h nên thể tích V2 = (πR2h) / 3
Từ đó suy ra: V1 = 3V2
Bài 20: Chọn A.
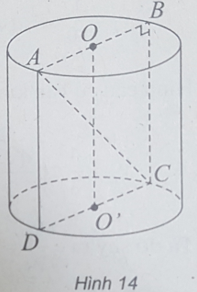
(h.14) Gọi O, O' là hai tâm của hai đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.
Do chu vi đáy của hình trụ đó bằng 6π (cm) nên bán kính đáy của hình trụ là: R = 3 (cm)
Vì thiết diện đi qua trục là một hình chữ nhật ABCD có AC = 10 (cm) và AB = 2R = 6 (cm) nên chiều cao của hình trụ là:
h = OO' = BC = 8 (cm)
Vậy thể tích khối trụ là: V = πR2h = 72π (cm3)
Bài 21: Chọn C.
Phương trình mặt phẳng theo đoạn chắn (ABC) là:
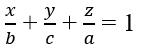
Bài 22: Chọn A.
Các mặt phẳng đôi một vuông góc và có một điểm chung.
Bài 23: Chọn D.
Hai đường thẳng d1 và d2 có hai vectơ chỉ phương tỉ lệ (-2; 2; -4) = -2(1; -1; 2) và có điểm chung M(0; 1; 1)
Suy ra d1 và d2 trùng nhau.
Bài 24: Chọn C.
Đường thẳng d có điểm chung M(1; 1; -1) với cả hai mặt phẳng (P), (Q) và d có vectơ chỉ phương (0; 1; 1) vuông góc với cả hai vectơ pháp tuyến của (P), (Q), do đó d nằm trên cả hai mặt phẳng (P), (Q). Suy ra d = (P) ∩ (Q).


