Giải SBT Toán 12: Đề toán tổng hợp ôn tập cuối năm
Hình học 12: Đề toán tổng hợp ôn tập cuối năm
VnDoc xin giới thiệu tới bạn đọc Giải SBT Toán 12: Đề toán tổng hợp ôn tập cuối năm. Tài liệu kèm theo lời giải chi tiết sẽ giúp các bạn giải bài tập Toán 12 hiệu quả hơn. Mời các bạn học sinh tham khảo.
Bài 1 trang 168 Sách bài tập Hình học 12: Cho lăng trụ ABC.A'B'C'
a) Tính tỉ số: 
\(\frac{V_{ACA'B'}}{V_{ABC.A'B'C'}}\)
b) Tính VACA'B' biết rằng tam giác ABC là tam giác đều cạnh bằng a, AA' = b và AA' tạo với (ABC) một góc bằng 60 o
Lời giải:
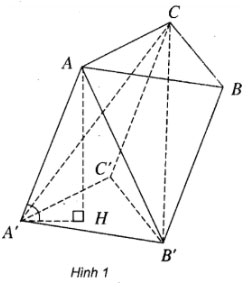
VACA'B' = VB'.ACA' = VB'.CA'C' = VC.A'B'C' = \(V=\frac{ABC.A'B'C'}{3}\)
Từ đó suy ra tỉ số phải tìm bằng \(\frac{1}{3}\)
b) Gọi H là chân đường cao đi qua A của lăng trụ. Khi đó góc (A'H, A'A) = 60o. Từ đó suy ra AH = \(\frac{(b\sqrt{3})}{2}\)
Ta cũng có: \(S_{A'B'C'}=\frac{\sqrt{3}}{4}a^2\)
Do đó: \(V=_{ABC.A'B'C'}=\frac{3}{8}a^2b\)
Từ đó suy ra: \(V_{ACA'B'}=\ \frac{1}{8}a^2b\)
Bài 2 trang 168 Sách bài tập Hình học 12: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của AB và AD, H là giao điểm của MD và NC. Biết rằng SH là đường cao của hình chóp đã cho và cạnh SC tạo với đáy hình chóp đó một góc bằng 60o
a) Thể tích hình chóp S.CDNM
b) Tính khoảng cách giữa DM và SC.
Lời giải:
a) Xét các hình vuông ABCD. Ta có hai tam giác vuông ADM và DCN bằng nhau nên ∠DMA = ∠CND. Từ đó suy ra DM ⊥ CN. Trong tam giác vuông CDN ta có:
CD2 = CH.CN ⇒ CH = \(\frac{2a}{\sqrt{5}}\)
SCDNM = SABCD - SAMN - SBCM = \(\frac{5a^2}{8}\)
VS.CDNM = \(\frac{a^{^3}\sqrt{15}}{12}\)
b) Gọi I là chân đường vuông góc kẻ từ H lên SC
Vì MD ⊥ (SCN), MD ∩ (SCN) = H nên d(MD, SC) = d(H, SC) = HI = HC.sin60o=\(\frac{a\sqrt{15}}{5}\)
Bài 3 trang 169 Sách bài tập Hình học 12: Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c.
a) Chứng minh rằng các đường vuông góc chung của các cặp cạnh đối diện đồng quy và đôi một vuông góc với nhau;
b) Tính VABCD theo a, b, c;
c) Chứng minh rằng tâm các mặt cầu nội tiếp và ngoại tiếp của tứ diện ABCD trùng nhau. Tính bán kính của các mặt cầu đó theo a, b, c.
Lời giải:
a) Gọi I và J lần lượt là trung điểm của AB và CD. Vì ΔACD = ΔBDC nên các tiếp tuyến tương ứng của chúng bằng nhau, do đó AJ = BJ. Từ đó suy ra IJ ⊥ AB. Tương tự, IJ ⊥ CD. Vậy IJ là đường vuông góc chung của AB và CD.
Làm tương tự đối với các cặp cạnh đối diện khác ta chứng minh được rằng đường nối trung điểm của các cặp cạnh đối diện là đường vuông góc chung của cặp cạnh đó. Do đó các đường đó đồng quy tại O là trung điểm của mỗi đường.
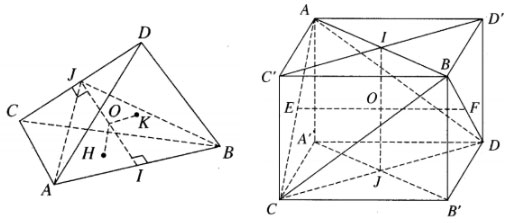
Gọi (P) là mặt phẳng qua AB và song song với CD, (Q) là mặt phẳng qua CD và song song với AB; A', B' lần lượt là hình chiếu vuông góc của A, B lên (Q); C', D' lần lượt là hình chiếu vuông góc của C, D lên (P). Dễ thấy AC'BD'.A'CB'D là hình hộp chữ nhật. Đường nối hai tâm của mỗi cặp mặt đối diện của hình hộp chữ nhật đó chính là đường vuông góc chung của các cặp cạnh đối diện của tứ diện ABCD. Do đó chúng đôi một vuông góc với nhau.
b) Đặt AC' = x, AD' = y, AA' = z.
Ta có:
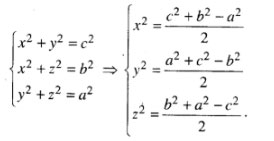
Từ đó suy ra \(V_{ABCD}=\frac{V_{_{AC'BD'.A'CB'D}}}{3}\)
c) Ta có O là tâm của hình hộp chữ nhật AC'BD'.A'C'B'D nên nó là tâm của mặt cầu ngoại tiếp tứ diện ABCD. Bán kính của mặt cầu ngoại tiếp tứ diện ABCD là
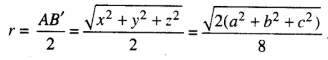
Gọi H và K theo thứ tự là chân đường vuông góc kẻ từ O đến (ABC) và (ABD). Vì OA = OB = OC nên HA = HB = HC, tương tự KA = KB = KD. Vì ΔABD = ΔBAC nên HA = KA. Do đó OH = OK. Tương tự, ta chứng minh được khoảng cách từ O đến các mặt của tứ diện ABCD bằng nhau nên O cũng là tâm của mặt cầu nội tiếp tứ diện ABCD.
Khi đó ta có VABCD = VOABC + VOBCD + VOCDA + VODAB
= 4VOABC =\(\frac{4r'S_{ABC}}{3}\)
Do đó:
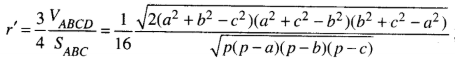
Trong đó \(p=\frac{a+b+c}{2}\)
Bài 4 trang 169 Sách bài tập Hình học 12:Cho hình nón tròn xoay (H) đỉnh S, đáy là hình tròn bán kính R, chiều cao bằng h.
Gọi (H') là hình trụ tròn xoay có đáy là hình tròn bán kính r (0 < r < R) nội tiếp (H).
a) Tính tỉ số thể tích của (H') và (H);
b) Xác định r để (H') có thể tích lớn nhất.
Lời giải:
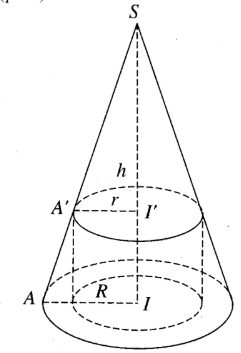
a) Giả sử đường cao SI của hình nón (H) cắt hai đáy của hình trụ (H') tại I và I'.
Khi đó \(\frac{r}{R}=\frac{SI'}{h}\)
Do đó
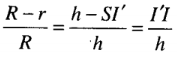
Từ đó suy ra \(I'I=\frac{h\left(R-r\right)}{R}\)
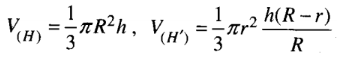
Do đó
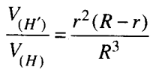
b) V(H') lớn nhất khi f(r) = r2(R - r) (với 0 < r < R) là lớn nhất. Khảo sát hàm số f(r), với 0 < r < R. Ta có f'(r) = 2Rr - 3r2 = 0, khi r = 0 (loại), hoặc \(r=\frac{2R}{3}\). Lập bảng biến thiên ta thấy f(r) đạt cực đại tại \(r=\frac{2R.}{3}\)
Khi đó
\(V_{\left(H'\right)}=\frac{4}{81}\pi R^2h\)
Bài 5 trang 169 Sách bài tập Hình học 12: Cho ba điểm A(1; 2; 1), B(2; -1; 1), C(0; 3; 1) và đường thẳng d:
\(\frac{x}{-3}=\frac{y}{-1}=\frac{z}{2}\)
a) Viết phương trình mặt phẳng (P) đi qua A, song song với d, sao cho khoảng cách từ B đến (P) bằng khoảng cách từ C đến (P).
b) Tìm tập hợp những điểm cách đều ba điểm A, B, C.
Lời giải:
a) Có hai trường hợp xảy ra:
Trường hợp 1:
(P) đi qua A, song song với hai đường thẳng d và BC. Vectơ chỉ phương của d là \(\underset{V}{\rightarrow}\)(-3; -1; 2) và \(\underset{BC}{\rightarrow}\)(-2; 4; 0).
Do đó nP→ = \(\underset{V}{\rightarrow}\) ∧ \(\underset{BC}{\rightarrow}\) = (-8; -4; -14).
Phương trình mặt phẳng (P) là: -8(x - 1) - 4(y - 2) - 14(z - 1) = 0 hay 4x + 2y + 7z - 15 = 0
Trường hợp 2:
(P) đi qua A, đi qua trung điểm F(1; 1; 1) của BC, và song song với d.
Ta có: \(\underset{FA}{\rightarrow}\)(0; 1; 0), \(\underset{FA}{\rightarrow}\) ∧ \(\underset{V}{\rightarrow}\)= (2; 0; 3).
Suy ra phương trình của (P) là: 2(x - 1) + 3(z - 1) = 0 hay 2x + 3z - 5 = 0.
b) Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.
Những điểm cách đều ba điểm A, B, C là giao tuyến Δ = (Q) ∩ (R).
(Q) đi qua trung điểm E(\(\frac{3}{2}\); \(\frac{1}{2}\); 1) của AB và có nQ→ = \(\underset{FA}{\rightarrow}\) (1; -3; 0) do đó phương trình của (Q) là: x - \(\frac{3}{2}\) - 3(y - \(\frac{1}{2}\)) = 0 hay x - 3y = 0
(R) đi qua trung điểm F(1; 1; 1) của BC và có nR→ = \(\underset{BC}{\rightarrow}\) = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0
Ta có: nQ→ ∧ nR→ = (0; 0; -2).
Lấy D(-3; -1; 0) thuộc (Q) ∩ (R)
Suy ra Δ là đường thẳng đi qua D và có vectơ chỉ phương \(\underset{u}{\rightarrow}\)(0; 0; 1)
nên có phương trình là:
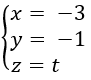
Bài 6 trang 169 Sách bài tập Hình học 12: Cho hai đường thẳng d, d' và M(2; -1; 0)
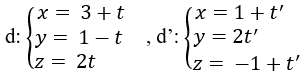
a) Chứng minh rằng d và d' chéo nhau.
b) Tìm tọa độ điểm A trên d và điểm B trên d' để M, A, B thẳng hàng.
Lời giải:
a) Ta chứng minh được d không song song với d' vì chúng có các vectơ chỉ phương không cùng phương.
Giải hệ phương trình
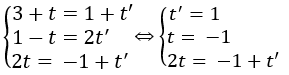
⇒ hệ phương trình vô nghiệm
Do đó d và d' chéo nhau.
b) Lấy A(3 + t; 1 - t; 2t) thuộc d và B(1 + t'; 2t'; -1 + t') thuộc d'. Ta có \(\underset{MA}{\rightarrow}\) = (1 + t; 2 - t; 2t), \(\underset{MB}{\rightarrow}\) = (-1 + t'; 1 + 2t'; -1 + t').
M, A, B thẳng hàng ⇔ \(\underset{MB}{\rightarrow}\) = k\(\underset{MA}{\rightarrow}\)
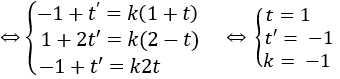
Từ đó suy ra A(4; 0; 2), B(0; -2; -2.
Bài 7 trang 169 Sách bài tập Hình học 12: Trong không gian Oxyz, cho mặt phẳng (P): x + 2y - z + 5 = 0 và hai điểm A(-2; -1; 1), B(6; 6; 5). Trong các đường thẳng qua A và song song với (P) hãy viết phương trình đường thẳng mà khoảng cách từ B đến đường thẳng đó là nhỏ nhất.
Lời giải:
Gọi (Q) là mặt phẳng đi qua A và song song với (P) thì phương trình của (Q) là (x + 2) + 2(y + 1) - (z - 1) = 0 hay x + 2y - z + 5 = 0. Gọi H là hình chiếu vuông góc của B lên (Q). Giả sử Δ là đường thẳng qua A và song song với (P), I là chân đường vuông góc kẻ từ B đến Δ. Khi đó I ∈ (Q) và BH ≤ BI.
Do đó AH chính là đường phải tìm.
Gọi d là đường thẳng đi qua B và vuông góc với (Q).
Phương trình của d là:
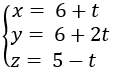
Để tìm giao điểm H = d ∩ (Q) ta thay phương trình của d vào phương trình của (Q), ta có:
6 + t + 2(6 + 2t) - (5 - t) + 5 = 0 ⇒ t = -3.
Do đó H = (3; 0; 8)
Phương trình đường thẳng AH là:
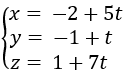
Bài 8 trang 169 Sách bài tập Hình học 12: Trong không gian Oxyz, cho mặt cầu (S): x2 + y2 + z2 - 2x + 4y + 2z - 19 = 0
và mặt phẳng (P): x - 2y + 2z - 12 = 0
a) Chứng minh rằng (P) cắt (S) theo một đường tròn.
b) Tìm tọa độ tâm và bán kính của đường tròn đó.
Lời giải:
a) Mặt cầu (S) tâm I(1; -2; -1) bán kính R = 5
d(I,(P)) = 3 < R
Do đó (P) cắt (S) theo một đường tròn, gọi đường tròn đó là (C).
b) Gọi d là đường thẳng qua I và vuông góc với (P). Phương trình của d là
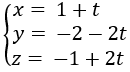
Tâm của (C) là điểm H = d ∩ (P). Để tìm H ta thay phương trình của d vào phương trình của (P).
Ta có: 1 + t - 2(-2 - 2t) + 2(-1 + 2t) - 12 = 0
Suy ra t = 1, do đó H = (2; -4; 1).
Bán kính của (C) bằng
\(\sqrt{R^2-IH^2}=\sqrt{25-9}=4\)
Bài 9 trang 170 Sách bài tập Hình học 12:
a) Hãy tìm tọa độ các đỉnh còn lại.
b) Chứng minh A'C ⊥ (BC'D)
c) Tìm tọa độ của chân đường vuông góc chung của B'D' và BC'.
Lời giải:
a) Dễ thấy C(1; 1; 0), B'(1; 0; 1), D'(0; 1; 1), C'(1; 1; 1), D'(0; 1; 1).
b) Ta có: \(\underset{A'C}{\rightarrow}\) = (1; 1; -1)
\(\underset{BC'}{\rightarrow}\) = (0; 1; 1)
\(\underset{BD}{\rightarrow}\) = \(\underset{B'D'}{\rightarrow}\) = (-1; 1; 0)
do đó \(\underset{A'C}{\rightarrow}\).\(\underset{BC'}{\rightarrow}\) = 0 và \(\underset{A'C}{\rightarrow}\).\(\underset{BD}{\rightarrow}\) = 0
Từ đó suy ra A'C ⊥ (BC'D).
c)
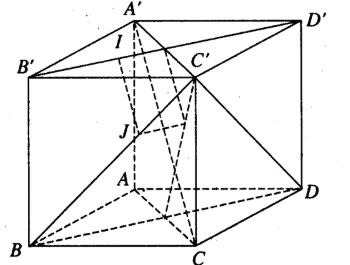
Gọi IJ là đường vuông góc chung của B'D' và BC', \(\underset{n_{1} }{\rightarrow}\) là vectơ pháp tuyến của mặt phẳng (P) qua B'D' và song song với AC', \(\underset{n_{2} }{\rightarrow}\) là vectơ pháp tuyến của mặt phẳng (Q) qua BC' và song song với A'C.
Khi đó \(\underset{n_{1} }{\rightarrow}\) = \(\underset{A'C}{\rightarrow}\) ∧ \(\underset{B'D'}{\rightarrow}\) = (1; 1; 2)
\(\underset{n_{2} }{\rightarrow}\) = \(\underset{A'C}{\rightarrow}\) ∧ \(\underset{BC'}{\rightarrow}\) = (2; -1; 1)
Phương trình của (P) là: (x - 1) + y + 2(z - 1) = 0 hay x + y + 2z - 3 = 0.
Phương trình của (Q) là: 2(x - 1) - y + z = 0 hay 2x - y + z - 2 = 0.
Phương trình của (B'D') là: x = 1 - t, y = t, z = 1.
Phương trình của (BC') là: x = 1, y = t, z = t.
I là giao điểm của đường thẳng B'D' và (Q), để tìm tọa độ của I ta thế phương trình đường thẳng B'D' vào phương trình của (Q)
Ta có: 2(1 - t) - t + 1 - 2 = 0, hay t = \(\frac{1}{3}\). Từ đó suy ra I\(\frac{2}{3}\); \(\frac{1}{3}\); 1)
Tương tự, ta tìm được J(1; \(\frac{2}{3}\); \(\frac{1}{3}\)).
Bài 10 trang 170 Sách bài tập Hình học 12: Trong không gian Oxyz, cho S(0; 0; 2), A(0; 0; 0), B(1; 2; 0), C(0; 2; 0)
a) Viết phương trình của mặt phẳng (P) qua A và vuông góc với SB;
b) Tìm tọa độ của các điểm B' là gia của (P) với đường thẳng SB, C' là giao của (P) với đường thẳng SC;
c) Tính thể tích tứ diện SAB'C';
d) Tìm điểm đối xứng với B qua mặt phẳng (P);
e) Chứng minh các điểm A, B, C, B', C' cùng thuộc một mặt cầu. Viết phương trình của mặt cầu đó và phương trình của mặt phẳng tiếp xúc với mặt cầu đó tại C'.
Lời giải:
a) \(\underset{SB}{\rightarrow}\)= (1; 2; -2). Phương trình (P): x + 2y - 2z = 0.
b) Phương trình đường thẳng SB: x - t, y = 2t, z = 2 - 2t. Để tìm B' ta giải hệ
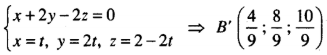
Tương tự, C'(0; 1; 1)
c)
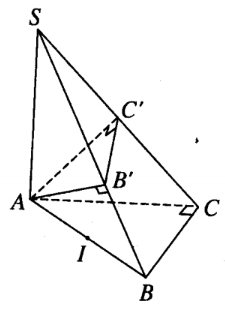
\(V_{SAB'C'}=\frac{4}{27}\)
d) Đường thẳng qua B và vuông góc với (P) có phương trình:
x = 1 + t; y = 2 + 2t; z = -2t.
Để tìm giao điểm Bo của đường thẳng này với (P) ta giả hệ
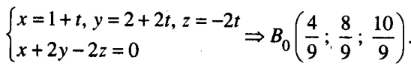
Từ đó suy ra điểm đối xứng với B qua (P) là
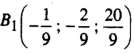
e) Dễ thấy \(\underset{BC}{\rightarrow}\) ⊥ \(\underset{AC}{\rightarrow}\), \(\underset{BC}{\rightarrow}\)⊥ \(\underset{AC}{\rightarrow}\), \(\underset{BB'}{\rightarrow}\) ⊥ \(\underset{AB'}{\rightarrow}\) nên A, B, C, B', C' cùng thuộc mặt cầu tâm I(\(\frac{1}{2}\); 1; 0) là trung điểm của AB, bán kính IA =\(\frac{(\sqrt{5})}{2}\)
Phương trình mặt cầu đó là
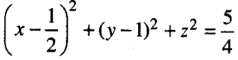
Vì điểm C' thuộc mặt cầu, nên mặt phẳng tiếp xúc với mặt cầu tại C' phải vuông góc với \(\underset{IC'}{\rightarrow}\) = (\(-\frac{1}{2}\); 0; 1). Phương trình của mặt phẳng đó là: x - 2(z - 1) = 0 hay x - 2z + 2 = 0.
