Giải bài tập Toán 12 Nâng cao Chương 1 bài 7: Khảo sát sự biến thiên và vẽ đồ thị hàm số của một số hàm phân thức hữu tỉ

Giải bài tập sgk Toán 12 Nâng cao bài 7 Đại số và Giải tích là tài liệu hướng dẫn các em giải các bài tập trong sách giáo khoa Toán 12 Nâng cao. Tài liệu sẽ giúp các em làm các dạng bài về Khảo sát sự biến thiên và vẽ đồ thị hàm số của một số hàm phân thức hữu tỉ.

Bài 49 trang 61 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số : \(y = {{x - 2} \over {2x + 1}}\)

b) Chứng minh rằng giao điểm I của hai đường tiệm cận của đồ thị là tâm đối xứng của đồ thị.

Giải

a) TXĐ:\(R\backslash \left\{ { - {1 \over 2}} \right\}\)
Ta có: \(\mathop {\lim }\limits_{x \to {{\left( { - {1 \over 2}} \right)}^ + }} y = - \infty và \mathop {\lim }\limits_{x \to {{\left( { - {1 \over 2}} \right)}^ - }} y = + \infty nên đường thẳng x = - {1 \over 2}\) là tiệm cận đứng của đồ thị.
Vì \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = {1 \over 2}\)nên đường thẳng \(y = {1 \over 2}\) là tiệm cận ngang của đồ thị.

\(y' = {{\left| \matrix{ 1\,\,\,\,\,\,\,\,\,2 \hfill \cr 2\,\,\,\,\,\,\,\,\,1 \hfill \cr} \right|} \over {{{\left( {2x + 1} \right)}^2}}} = {5 \over {{{\left( {2x + 1} \right)}^2}}} > 0 với mọi x \ne - {1 \over 2}\)

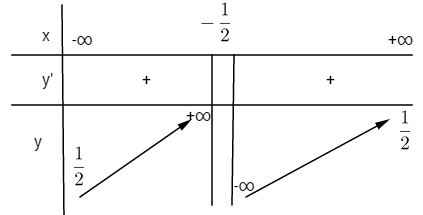
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - {1 \over 2}} \right)\)và \(\left( { - {1 \over 2}; + \infty } \right)\)

Đồ thị cắt trục tung tại điểm (0;-2) và cắt trục hoành tại điểm (2;0).

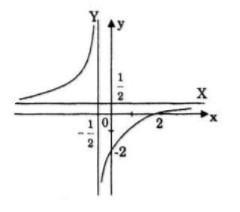
b) Giao điểm hai tiệm cận của đồ thị \(I\left( { - {1 \over 2};{1 \over 2}} \right)\)
Công thức đổi trục tịnh tiến theo vectơ \(I\left( { - {1 \over 2};{1 \over 2}} \right)\)\(I\left( { - {1 \over 2};{1 \over 2}} \right)\) là:

\(\left\{ \matrix{ x = X - {1 \over 2} \hfill \cr y = Y + {1 \over 2} \hfill \cr} \right.\)

Phương trình của đồ thị (C) đối với trục IXY:

\(Y + {1 \over 2} = {{X - {1 \over 2} - 2} \over {2\left( {X - {1 \over 2}} \right) + 1}} \Leftrightarrow Y + {1 \over 2} = {{X - {5 \over 2}} \over {2X}} \Leftrightarrow Y = - {5 \over {4X}}\)

Đây là hàm số lẻ nên đồ thị nhận I làm tâm đối xứng.

Bài 50 trang 61 sgk Toán 12 Nâng cao Đại số và Giải tích

Khảo sát sự biến thiên và vẽ đồ thị hàm số sau:

a)\(y = {{x + 1} \over {x - 1}}\)

b) \(y = {{2x + 1} \over {1 - 3x}}\)

Giải

a) TXĐ: \(D =\mathbb R\backslash \left\{ 1 \right\}\)

\(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty ;\,\,\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty\) nên x = 1 là tiệm cận đứng.

\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } = 1\) nên y=1 là tiệm cận ngang.

\(y = {{\left| \matrix{ 1\,\,\,\,\,\,\,\,\,\,\,1 \hfill \cr 1\,\,\,\,\,\,\, - 1 \hfill \cr} \right|} \over {{{\left( {x - 1} \right)}^2}}} = {{ - 2} \over {{{\left( {x - 1} \right)}^2}}} < 0 với mọi x \ne 1\)

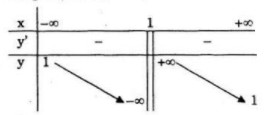
Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;1} \right)\)và \(\left( {1; + \infty } \right)\)

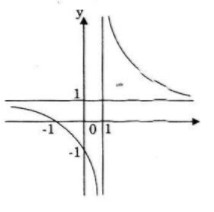
Đồ thị hàm số cắt trục tung tại điểm (0;-1) cắt trục hoành tại điểm (-1;0).

Đồ thị nhận giao điểm hai tiệm cận I(1;1) làm tâm đối xứng.

b) TXĐ: \(D =\mathbb R\backslash \left\{ {{1 \over 3}} \right\}\)

\(\mathop {\lim }\limits_{x \to {{\left( {{1 \over 3}} \right)}^ + }} y = - \infty ;\,\mathop {\lim }\limits_{x \to {{\left( {{1 \over 3}} \right)}^ - }} y = - \infty\)nên\(x = {1 \over 3}\) là tiệm cận đứng.
Vì\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } = - {2 \over 3} nên y = - {2 \over 3}\) là tiệm cận ngang.

\(y = {{\left| \matrix{ 2\,\,\,\,\,\,\,1 \hfill \cr - 3\,\,\,\,1 \hfill \cr} \right|} \over {{{\left( {1 - 3x} \right)}^2}}} = {5 \over {{{\left( {1 - 3x} \right)}^2}}} > 0 với mọi(x \ne {1 \over 3}\)

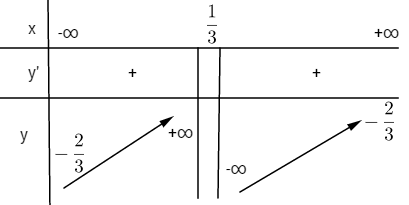
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;{1 \over 3}} \right)\)và \(\left( {{1 \over 3}; + \infty } \right)\)
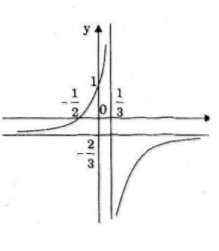
Đồ thị cắt trục tung tại điểm (0;1) và cắt trục hoành tại điểm \(\left( { - {1 \over 2};0} \right)\)
Đồ thị nhận giao điểm hai tiệm cận \(I\left( {{1 \over 3};{1 \over 2}} \right)\)làm tâm đối xứng.

Bài 51 trang 61 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số:\(y = {{2{x^2} + 5x + 4} \over {x + 2}}\)

b) Chứng minh rằng giao điểm I của đường tiệm cận của đồ thị là tâm đối xứng của đồ thị.

c) Tùy theo các giá trị của m, hãy biện luận số nghiệm của phương trình:

\({{2{x^2} + 5x + 4} \over {x + 2}} + m = 0\)

Giải

a) TXĐ:\(D =\mathbb R\backslash \left\{ { - 2} \right\}\)

\(\mathop {\lim }\limits_{x \to - {2^ + }} y = + \infty ;\,\,\mathop {\lim }\limits_{x \to - {2^ - }} y = - \infty\) nên x = -2 là tiệm cận đứng.

Ta có: \(y = 2x + 1 + {2 \over {x + 2}}\)

\(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {2x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {2 \over {x + 2}} = 0\) nên \(y = 2x + 1\) là tiệm cận xiên

\(\eqalign{ & y' = 2 - {2 \over {{{\left( {x + 2} \right)}^2}}} = {{2\left[ {{{\left( {x + 2} \right)}^2} - 1} \right]} \over {{{\left( {x + 2} \right)}^2}}} = {{2\left( {x + 1} \right)\left( {x + 3} \right)} \over {{{\left( {x + 2} \right)}^2}}} \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = - 1;\,\,y\left( { - 1} \right) = 1 \hfill \cr x = - 3;\,\,y\left( { - 3} \right) = - 7 \hfill \cr} \right. \cr}\)

Bảng biến thiên:

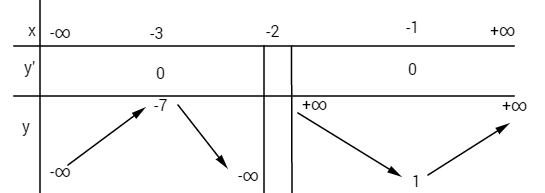
Điểm đặc biệt: \(x = 0 \Rightarrow y = 2\)

b) Giao điểm hai đường tiệm cận của đồ thị là nghiệm của hệ.

\(\left\{ \matrix{ x = - 2 \hfill \cr y = 2x + 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 2 \hfill \cr y = - 3 \hfill \cr} \right. Vậy I\left( { - 2; - 3} \right)\)

Công thức đổi trục tịnh tiến theo véc tơ \(\overrightarrow {OI}\) là

\(\left\{ \matrix{x = X - 2 \hfill = Y - 3 \hfill } \right.\)

Ta có

\(\eqalign{ & Y - 3 = 2(X - 2) + 1 + {2 \over {X - 2 + 2}} \cr & \Leftrightarrow Y - 3 = 2X - 4 + 1 + {2 \over X} \cr & \Leftrightarrow Y = 2X + {2 \over X} \cr}\)

Hàm số là hàm số lẻ nên đồ thị của hàm số nhận gốc I làm tâm đối xứng.

c) Ta có:\({{2{x^2} + 5x + 4} \over {x + 2}} + m = 0 \Leftrightarrow {{2{x^2} + 5x + 4} \over {x + 2}} = - m\)

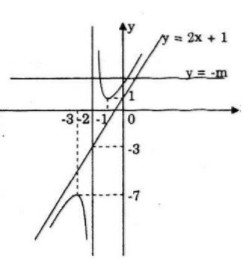
Số nghiệm của phương trình chính là số giao điểm của đồ thị (C) hàm số và đường thẳng y = -m, vào đồ thị ta có:
+) - m< -7 hoặc\(–m>1\ \Leftrightarrow m > 7 hoặc m< -1\) : phương trình có 2 nghiệm.

+) -m=-7 hoặc \(–m = 1 \Leftrightarrow m = 7 hoặc m = -1\): phương trình có 1 nghiệm.

+) - 7<m< 1 => -1 < m < 7: phương trình vô nghiệm.

Bài 52 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a)\(y = {{{x^2} - 3x + 6} \over {x - 1}}\)

b) \(y = {{2{x^2} - x + 1} \over {1 - x}}\)

c) \(y = {{2{x^2} + 3x - 3} \over {x + 2}}\)

d) \(y = - x + 2 + {1 \over {x - 1}}\)

Giải

a)\(y = x- 2 + {4 \over {x - 1}}\)
TXĐ: \(D =\mathbb R\backslash \left\{ 1 \right\}\)

\(\mathop {\lim }\limits_{x \to {1^ + }} y = + \infty ;\,\mathop {\lim }\limits_{x \to {1^ - }} y = - \infty\)nên x = 1 là tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 2} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {4 \over {x - 1}} = 0\) nên y = x – 2 là tiệm cận xiên.

\(\eqalign{ & y' = 1 - {4 \over {{{\left( {x - 1} \right)}^2}}} = {{{{\left( {x - 1} \right)}^2} - 4} \over {{{\left( {x - 1} \right)}^2}}} = {{\left( {x - 3} \right)\left( {x + 1} \right)} \over {{{\left( {x - 1} \right)}^2}}} \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = - 1;\,\,\,y\left( { - 1} \right) = -5 \hfill \cr x = 3;\,\,\,y\left( 3 \right) = 3 \hfill \cr} \right. \cr}\)

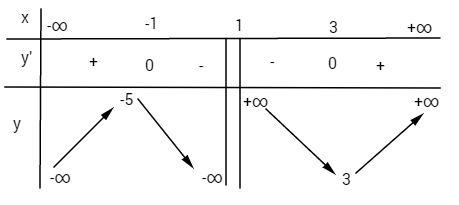
Điểm đặc biệt: \(x = 0 \Rightarrow y = - 6\)

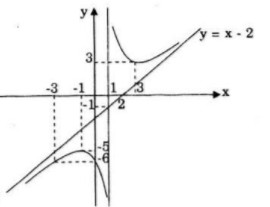
Đồ thị nhận giao điểm I(1;-1) của hai đường tiệm cận làm tâm đối xứng.

b) \(y = {{ - 2{x^2} + x - 1} \over {x - 1}}\)

\(y = - 2x - 1 - {2 \over {x - 1}}\)

TXĐ: \(D =\mathbb R\backslash \left\{ 1 \right\}\)

Tiệm cận đứng: x = 1

Tiệm cận xiên: y = -2x – 1

\(\eqalign{ & y' = - 2 + {2 \over {{{\left( {x - 1} \right)}^2}}} = {{ - 2{{\left( {x - 1} \right)}^2} + 2} \over {{{\left( {x - 1} \right)}^2}}} = {{ - 2{x^2} + 4x} \over {{{\left( {x - 1} \right)}^2}}} \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 0;\,\,\,\,\,y\left( 0 \right) = 1 \hfill \cr x = 2;\,\,\,\,\,\,y\left( 2 \right) = - 7 \hfill \cr} \right. \cr}\)

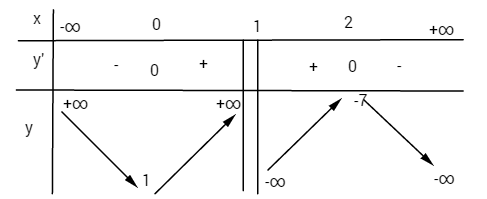
Điểm đặc biệt

\(x = 0 \Rightarrow y = 1\)

\(x = -1 \Rightarrow y = 2\)

Đồ thị:

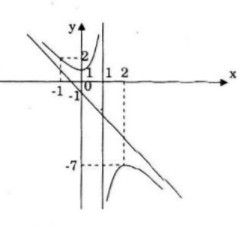
Đồ thị nhận I(1;-3) làm tâm đối xứng.

c) \(y = 2x - 1 - {1 \over {x + 2}}\)

TXĐ: \(D =\mathbb R\backslash \left\{ { - 2} \right\}\)

Tiệm cận đứng: x = 2

Tiệm cận xiên: y = 2x -1

\(D =\mathbb R\backslash \left\{ { - 2} \right\}\)

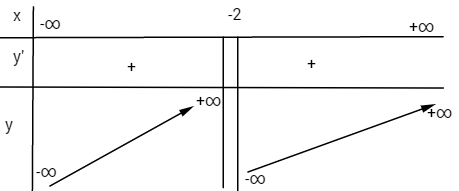
• Điểm đặc biệt: \(x = 0 \Rightarrow y = - {3 \over 2}\)

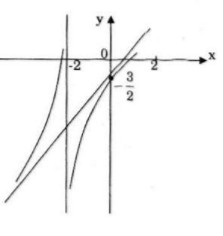
Đồ thị nhận I(-2; -5) làm tâm đối xứng.
d) \(y = - x + 2 + {1 \over {x - 1}}\)

TXĐ: \(D =\mathbb R\backslash \left\{ 1 \right\}\)

Tiệm cận đứng: x = 1

Tiệm cận xiên y = -x +2

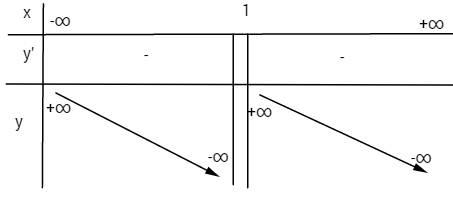
Điểm đặc biệt: \(x = 0 \Rightarrow y = 1\)

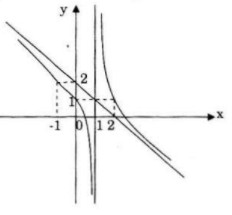
Đồ thị nhận điểm I(1;-1) làm tâm đối xứng.

Bài 53 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = {{x + 1} \over {x - 2}}\)

b) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại giao điểm A của đồ thị với trục tung.

c) Viết phương trinh tiếp tuyến của đồ thị song song với tiếp tuyến tại điểm A.

Giải

a) TXĐ: \(D =\mathbb R\backslash \left\{ 2 \right\}\)

Tiệm cận đứng x = 2; tiệm cận ngang y = 1.

\(y' = {{ - 3} \over {{{\left( {x - 2} \right)}^2}}} < 0 với mọi x \ne 2\)

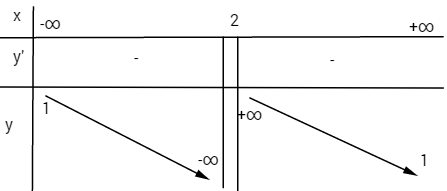
Điểm đặc biệt: \(A\left( {0; - {1 \over 2}} \right),\,B\left( { - 1;0} \right)\)

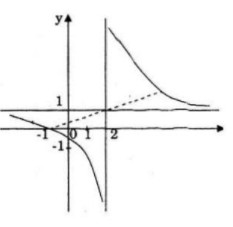
Đồ thị nhận điểm I(2;1) làm tâm đối xứng.

b) Giao điểm của đồ thị với trục tung\(A\left( {0; - {1 \over 2}} \right) y'\left( 0 \right) = - {3 \over 4}\)

Phương trình tiếp tuyến của đồ thị tại A là:

\(y + {1 \over 2} = - {3 \over 4}\left( {x - 0} \right) \Leftrightarrow y = - {3 \over 4}x - {1 \over 2}\)

c) Giả sử M là tiếp điểm của tiếp tuyến song song với tiếp tuyến tại A ta có:

\(y'\left( {{x_M}} \right) = - {3 \over 4} \Leftrightarrow {{ - 3} \over {{{\left( {{x_M} - 2} \right)}^2}}} = - {3 \over 4} \Leftrightarrow {\left( {{x_M} - 2} \right)^2} = 4\)

\(\Leftrightarrow \left[ \matrix{ {x_M} - 2 = 2 \hfill \cr {x_M} - 2 = - 2 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ {x_M} = 4 \hfill \cr {x_M} = 0\,\,(\text{ loại vì }{x_A} = 0) \hfill \cr} \right. y\left( 4 \right) = {5 \over 2}. Vậy M\left( {4;{5 \over 2}} \right)\)

Phương trình tiếp tuyến tại điểm M là: \(y - {5 \over 2} = - {3 \over 4}\left( {x - 4} \right) \Leftrightarrow y = - {3 \over 4}x + {{11} \over 2}\)

Bài 54 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số\(y = 1 - {1 \over {x + 1}}\)
b) Từ đồ thị \((H)\) suy ra cách vẽ đồ thị của hàm số \(y = 1 + {1 \over {x + 1}}\)

Giải

a)\(y = {x \over {x + 1}}\)

TXĐ: \(D = R\backslash \left\{ { - 1} \right\}\)

Tiệm cận đứng x = -1; tiệm cận ngang y = 1.

\(y' = {1 \over {{{\left( {x + 1} \right)}^2}}} > 0 với mọi x \ne - 1\)

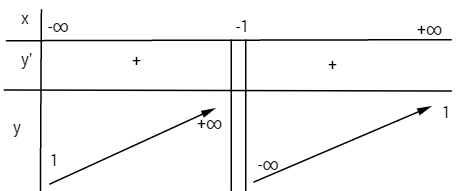
Điểm đặc biệt

\(\eqalign{ & x = 0 \Rightarrow y = 0 \cr & x = 1 \Rightarrow y = {1 \over 2} \cr}\)

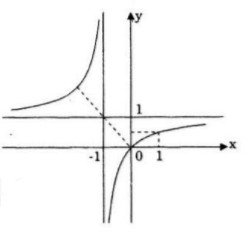
Đồ thị nhận I(-1;1) làm tâm đối xứng.

b) Ta có \(y = - 1 + {1 \over {x + 1}} = {{ - x} \over {x + 1}}\)

Do đó đồ thị của hàm số \(y = - 1 + {1 \over {x + 1}}\) là hình đối xứng của H qua trục hoành.

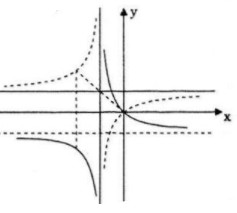
Bài 55 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = x - {2 \over {x - 1}}\)

b) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho biết rằng tiếp tuyến đó đi qua điểm (3;3).

Giải

a) Tập xác định: \(D = R\backslash \left\{ 1 \right\}\)

\(y' = 1 + {2 \over {{{\left( {x - 1} \right)}^2}}} > 0,\forall x \in D\)

Vậy hàm số đồng biến trên khoảng \(( - \infty ;1)\) và \((1; + \infty )\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to {1^ - }} y = + \infty \cr & \mathop {\lim }\limits_{x \to {1^ + }} y = - \infty \cr}\)

Do đó x=1 là tiệm cận đứng.

\(\mathop {\lim }\limits_{x \to \pm \infty } (y - x) = \mathop {\lim }\limits_{x \to \pm \infty } \left( { - {2 \over {x - 1}}} \right) = 0\)

Vậy y=x là tiệm cận xiên.

Bảng biến thiên:

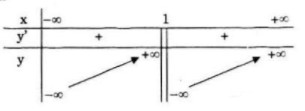
Đồ thị giao Ox tại (-1;0),(2;0)

Đồ thị giao (Oy tại (0;2)

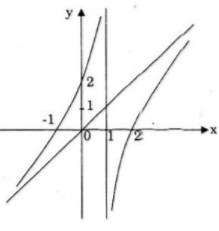
b) Ta có: \(y' = 1 + {2 \over {{{\left( {x - 1} \right)}^2}}}\)

Phương trình tiếp tuyến với đồ thị hàm số đã cho tại điểm \(M\left( {{x_o};{y_o}} \right) \in \left( C \right)\) là:

\(\left( d \right):\,y - {x_o} + {2 \over {{x_o} - 1}} = \left[ {1 + {2 \over {{{\left( {{x_o} - 1} \right)}^2}}}} \right]\left( {x - {x_o}} \right)\,\left( {x \ne 1} \right)\)

Vì \(\left( {3;3} \right) \in d nên 3 - {x_o} + {2 \over {{x_o} - 1}} = {{{{\left( {{x_o} - 1} \right)}^2} + 2} \over {{{\left( {{x_o} - 1} \right)}^2}}}\left( {3 - {x_o}} \right)\)

\(\eqalign{ & \Leftrightarrow \left( {3 - {x_o}} \right){\left( {{x_o} - 1} \right)^2} + 2\left( {{x_o} - 1} \right) = \left( {{x_o} - 2{x_o} + 3} \right)\left( {3 - {x_o}} \right) \cr & \Leftrightarrow {x_o} = 2;\,{y_o} = y\left( 2 \right) = 0 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y'\left( 2 \right) = 3 \cr}\)

Vậy phương trình tiếp tuyến cần tìm là: \(y = 3\left( {x - 2} \right)\) hay y = 3x - 6.

Bài 56 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị C của hàm số \(y = {{{x^2}} \over {x + 1}}\)

b) Từ đồ thị C suy ra cách vẽ đồ thị của hàm số \(y = {{{x^2}} \over {\left| {x + 1} \right|}}\)

Giải

a) \(D = R\backslash \left\{ { - 1} \right\}\)

\(\eqalign{ & y' = {{{x^2} + 2x} \over {{{\left( {x + 1} \right)}^2}}} \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = - 2 \hfill \cr} \right. \cr}\)

Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\)và \(\left( {0; + \infty } \right)\)

Hàm số nghịch biến trên khoảng (-2;-1) và (1;0)

Hàm số đạt cực đại tại x=-2, \(y_{CĐ}=-4\)

Hàm số đạt cực tiểu tại x=0, \(y_{CT}=0\)

\(\mathop {\lim }\limits_{x \to - {1^ + }} y = + \infty \mathop {\lim }\limits_{x \to - {1^ - }} y = - \infty\)

Vậy x=-1 là tiệm cận đứng.

\(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - (x - 1)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{1 \over {x + 1}}} \right) = 0\)

Vậy y= x-1 là tiệm cận xiên.

Bảng biến thiên

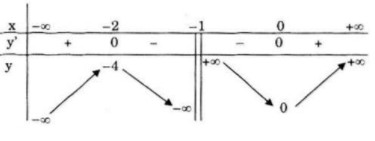
Đồ thị

Đồ thị giao Ox, Oy tại O(0;0)

\(x=-2\rightarrow y=-4\)

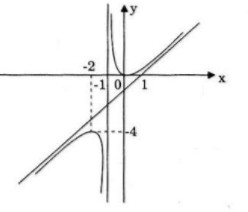
b) Ta có

\(y = {{{x^2}} \over {\left| {x + 1} \right|}} = \left\{ \matrix{ {{{x^2}} \over {x + 1}}\,\,\text{nếu} \,x > - 1 \hfill \cr - {{{x^2}} \over {x + 1}}\,\,\text{ nếu }\,x < - 1 \hfill \cr} \right.\)

Giữ nguyên phần đồ thị C ở bên phải tiệm cận đứng x = -1 và lấy đối xứng của phần C bên trái tiệm cận đứng qua trục hoành.

Đây là tài liệu rất cần thiết để các em tham khảo trong quá trình làm bài tập. Tài liệu chủ yếu cung cấp cho các em phương pháp giải các bài tập hiệu quả, ngắn gọn và dễ hiểu. Các em có thể tự ôn bài ở nhà, củng cố và nắm vững kiến thức. Các em có thể tham khảo thêm Giải bài tập Toán 12 hoặc Giải vở bài tập Toán 12 để làm quen với nhiều dạng bài khác nhau.

VnDoc xin giới thiệu tới các em Giari bài tập sgk Toán 12 Nâng cao bài 7 Đại số và Giải tích. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt kết quả cao trong học tập và trong các kì thi quan trọng. Các em có thể tham khảo thêm các tài liệu khác tại Tài liệu học tập lớp 12 do VnDoc đã tổng hợp và đăng tải như: Trắc nghiệm Tiếng Anh 12, Trắc nghiệm Hóa học 12, Trắc nghiệm Sinh học 12,...