VnDoc.com

Giải bài tập Toán Nâng cao Đại số và Giải tích 12 bài 2

Cực trị của hàm số

Bài trước

Bài sau

Giải bài tập Toán 12 Nâng cao Đại số và Giải tích 12 là tài liệu tham khảo hướng dẫn các em giải các bài tập trong sách giáo khoa Toán 12 chương trình Nâng cao. Tài liệu được trình bày cụ thể, rõ ràng giúp các em dễ dàng nắm bắt kiến thức.

Giải bài tập SGK Toán 12 Nâng cao bài 2

Bài 11 sgk trang 16, 17 Toán Nâng cao 12 Đại số và giải tích
Bài 12 sgk trang 17 Toán Nâng cao 12 Đại số và giải tích
Bài 13 sgk trang 17 Toán Nâng cao 12 Đại số và giải tích
Bài 14 sgk trang 17 Toán Nâng cao 12 Đại số và giải tích
Bài 15 sgk trang 17 Toán Nâng cao 12 Đại số và giải tích

Bài 11 sgk trang 16, 17 Toán Nâng cao 12 Đại số và Giải tích

Tìm cực trị của các hàm số sau:

a) $f\left( x \right) = {1 \over 3}{x^3} + 2{x^2} + 3x - 1$ $f\left( x \right) = {1 \over 3}{x^3} + 2{x^2} + 3x - 1$

b) $f\left( x \right) = {1 \over 3}{x^3} - {x^2} + 2x - 10$ $f\left( x \right) = {1 \over 3}{x^3} - {x^2} + 2x - 10$

c) $f\left( x \right) = x + {1 \over x}$ $f\left( x \right) = x + {1 \over x}$

d) $f\left( x \right) = \left| x \right|\left( {x + 2} \right);$ $f\left( x \right) = \left| x \right|\left( {x + 2} \right);$

e) $f\left( x \right) = {{{x^5}} \over 5} - {{{x^3}} \over 3} + 2$ $f\left( x \right) = {{{x^5}} \over 5} - {{{x^3}} \over 3} + 2$

f) $f\left( x \right) = {{{x^2} - 3x + 3} \over {x - 1}}$ $f\left( x \right) = {{{x^2} - 3x + 3} \over {x - 1}}$

Giải

a) TXĐ: $D=\mathbb R$ $D=\mathbb R$

$f'\left( x \right) = {x^2} + 4x + 3;\,f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \hfill \cr x = - 3 \hfill \cr} \right.;f\left( { - 1} \right) = - {7 \over 3};\,f\left( { - 3} \right) = - 1$

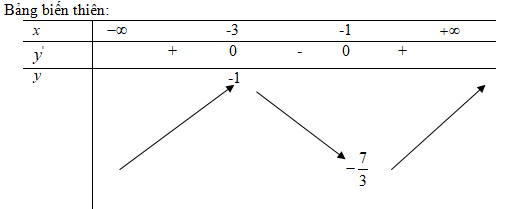
Giải bài tập sgk Toán 12 Nâng cao bài 11 câu a

Hàm số đạt cực đại tại điểm $x = - 3$, giá trị cực đại của hàm số là $f\left( { - 3} \right) = - 1$ $f\left( { - 3} \right) = - 1$

Hàm số đạt cực tiểu tại điểm x= -1, giá trị cực tiểu của hàm số là $f\left( { - 1} \right) = - {7 \over 3}$ $f\left( { - 1} \right) = - {7 \over 3}$

b) TXĐ: $D=\mathbb R$ $D=\mathbb R$

$f'\left( x \right) = {x^2} - 2x + 2 > 0$ với mọi $x \in\mathbb R (vì a > 0,\Delta$ $x \in\mathbb R (vì a > 0,\Delta ' < 0)$

Hàm số đồng biến trên $\mathbb R$ $\mathbb R$ , không có cực trị.

c) TXĐ: $D = \mathbb R\backslash \left\{ 0 \right\}$ $D = \mathbb R\backslash \left\{ 0 \right\}$

$f'\left( x \right) = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}};f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = 1\,\,\,\,;f\left( 1 \right) = 2 \hfill \cr x = - 1;f\left( { - 1} \right) = - 2 \hfill \cr} \right.$

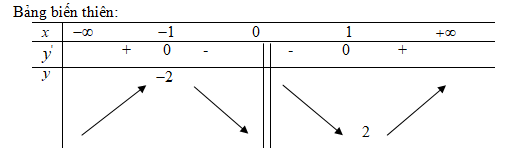
Giải bài tập sgk Toán 12 Nâng cao bài 11 câu c

Hàm số đạt cực đại tại điểm $x=-1$, giá trị cực đại $f\left( { - 1} \right) = - 2$ $f\left( { - 1} \right) = - 2$ Hàm số đạt cực tiểu tại điểm x=1, giá trị cực tiểu $f\left( 1 \right) = 2$ $f\left( 1 \right) = 2$

d) TXĐ: $D=\mathbb R Hàm số liên tục trên \mathbb R$ $D=\mathbb R Hàm số liên tục trên \mathbb R$

$f\left( x \right) = \left\{ \matrix{ x\left( {x + 2} \right)\,\,\,\,\,\,\,x \ge 0 \hfill \cr - x\left( {x + 2} \right)\,\,\,\,\,x < 0\, \hfill \cr} \right.$ $f\left( x \right) = \left\{ \matrix{ x\left( {x + 2} \right)\,\,\,\,\,\,\,x \ge 0 \hfill \cr - x\left( {x + 2} \right)\,\,\,\,\,x < 0\, \hfill \cr} \right.$

Với $x > 0:\,f$ $x > 0:\,f'\left( x \right) = 2x + 2 > 0 với mọi x>0$

Với $x < 0:\,f$ $x < 0:\,f'\left( x \right) = - 2x - 2\,;\,\,f'\left( x \right) = 0 \Leftrightarrow x = - 1,f\left( { - 1} \right) = 1$

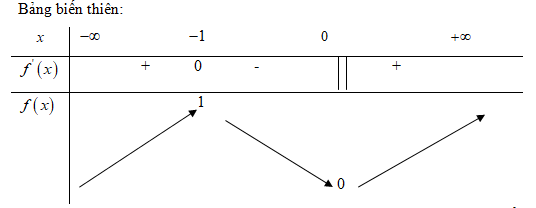
Giải bài tập sgk Toán 12 Nâng cao bài 11 câu d

Hàm số đạt cực đại tại x= -1, giá trị cực đại $f\left( { - 1} \right) = 1$ $f\left( { - 1} \right) = 1$. Hàm số đạt cực tiểu tại điểm x=0, giá trị cực tiểu $f\left( 0 \right) = 0$ $f\left( 0 \right) = 0$

e) TXĐ: $D=\mathbb R$ $D=\mathbb R$

$f'\left( x \right) = {x^4} - {x^2} = {x^2}\left( {{x^2} - 1} \right)f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = 0;f\left( 0 \right) = 2 \hfill \cr x = - 1;f\left( { - 1} \right) = {{32} \over {15}} \hfill \cr x = 1;f\left( 1 \right) = {{28} \over {15}} \hfill \cr} \right.$

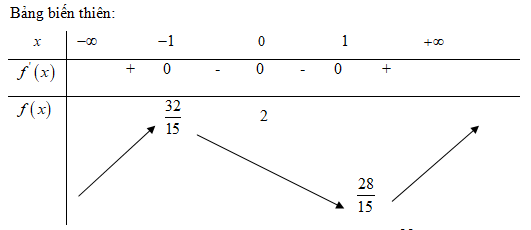
Giải bài tập sgk Toán 12 Nâng cao bài 11 câu e

Hàm số đạt cực đại tại điểm x=-1, giá trị cực đại $f\left( { - 1} \right) = {{32} \over {15}}$ $f\left( { - 1} \right) = {{32} \over {15}}$

Hàm số đạt cực tiểu tại x=1, giá trị cực tiểu $f\left( 1 \right) = {{28} \over {15}}$ $f\left( 1 \right) = {{28} \over {15}}$

f) TXĐ: $D = {\bf{R}}\backslash \left\{ 1 \right\}$ $D = {\bf{R}}\backslash \left\{ 1 \right\}$

$y'\left( x \right) = {{\left( {2x - 3} \right)\left( {x - 1} \right) - \left( {{x^2} - 3x + 3} \right)} \over {{{\left( {x - 1} \right)}^2}}} = {{{x^2} - 2x} \over {{{\left( {x - 1} \right)}^2}}}(f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = 0;f\left( 0 \right) = - 3 \hfill \cr x = 2;f\left( 2 \right) = 1 \hfill \cr} \right.$

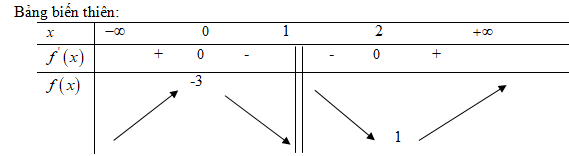
Giải bài tập sgk Toán 12 Nâng cao bài 11 câu f

Hàm số đạt cực đại tại điểm x=0, giá trị cực đại $f\left( 0 \right) = - 3$ $f\left( 0 \right) = - 3$

Hàm số đạt cực tiểu tại điểm x=2, giá trị cực tiểu $f\left( 2 \right) = 1$ $f\left( 2 \right) = 1$

Bài 12 sgk trang 17 Toán Nâng cao 12 Đại số và Giải tích

Tìm cực trị của các hàm số sau:

a) $y=x\sqrt{4-x^2}$ $y=x\sqrt{4-x^2}$

$b)\ y=\sqrt{8-x^2}$ $b)\ y=\sqrt{8-x^2}$

c) $y=x-\sin2x+2$ $y=x-\sin2x+2$

$d)\ y=3-2\cos x-\cos2x$ $d)\ y=3-2\cos x-\cos2x$

Giải

a) Tập xác định: $D = \left[ { - 2;2} \right]$ $D = \left[ { - 2;2} \right]$

$y' = \sqrt {4 - {x^2}} + x.{{ - x} \over {\sqrt {4 - {x^2}} }} = {{4 - {x^2} - {x^2}} \over {\sqrt {4 - {x^2}} }} = {{4 - 2{x^2}} \over {\sqrt {4 - {x^2}} }}y' = 0 \Leftrightarrow 4 - 2{x^2} = 0 \Leftrightarrow x = \pm \sqrt 2\left( { - \sqrt 2 } \right) = - 2;y\left( {\sqrt 2 } \right) = 2$

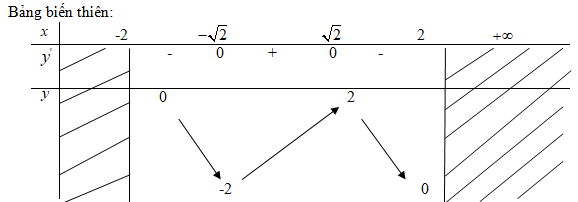
Giải bài tập sgk Toán 12 Nâng cao câu a

Hàm số đạt cực tiểu tại điểm $x = - \sqrt 2$ $x = - \sqrt 2$; giá trị cực tiểu $y\left( { - \sqrt 2 } \right) = - 2$ $y\left( { - \sqrt 2 } \right) = - 2$

Hàm số đạt cực đại tại điểm $x = \sqrt 2$ $x = \sqrt 2$; giá trị cực đại $y\left( {\sqrt 2 } \right) = 2$ $y\left( {\sqrt 2 } \right) = 2$

b) TXĐ: $D = \left[ { - 2\sqrt 2 ;2\sqrt 2 } \right]$ $D = \left[ { - 2\sqrt 2 ;2\sqrt 2 } \right]$

$y' = {{ - x} \over {\sqrt {8 - {x^2}} }};\,y' = 0 \Leftrightarrow x = 0;\,y\left( 0 \right) = 2\sqrt 2$

Bảng biến thiên:

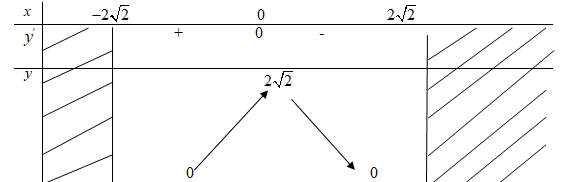
Giải bài tập Toán 12 Nâng cao bài 12 câu b

Hàm số đạt cực đại tại điểm x=0, giá trị cực đại $y\left( 0 \right) = 2\sqrt 2$ $y\left( 0 \right) = 2\sqrt 2$

c) Áp dụng quy tắc 2.

TXĐ: $D=\mathbb R$ $D=\mathbb R$

$\,y$ $\,y' = 1 - 2\cos 2x;y' = 0 \Leftrightarrow \cos 2x = {1 \over 2} = \cos {\pi \over 3} \Leftrightarrow x = \pm {\pi \over 6} + k\pi ,k \in {\mathbb {Z}}(y'' = 4\sin 2x$

* Ta có:$y''\left( {{\pi \over 6} + k\pi } \right) = 4\sin \left( { - {\pi \over 3}} \right) = - 2\sqrt 3 < 0$

Do đó hàm số đạt cực đại tại các điểm $x = - {\pi \over 6} + k\pi ,k \in {\mathbb{Z}}$ $x = - {\pi \over 6} + k\pi ,k \in {\mathbb{Z}}$ giá trị cực đại

$y\left( { - {\pi \over 6} + k\pi } \right) = - {\pi \over 6} + k\pi + {{\sqrt 3 } \over 2} + 2y$ $y\left( { - {\pi \over 6} + k\pi } \right) = - {\pi \over 6} + k\pi + {{\sqrt 3 } \over 2} + 2y''\left( {{\pi \over 6} + k\pi } \right) = 4\sin \left( {{\pi \over 3}} \right) = 2\sqrt 3 > 0$

Do đó hàm số đạt cực tiểu tại các điểm $x = {\pi \over 6} + k\pi ,k \in {\mathbb{Z}}$ $x = {\pi \over 6} + k\pi ,k \in {\mathbb{Z}}$ giá trị cực tiểu:

$y\left( {{\pi \over 6} + k\pi } \right) = {\pi \over 6} + k\pi - {{\sqrt 3 } \over 2} + 2$ $y\left( {{\pi \over 6} + k\pi } \right) = {\pi \over 6} + k\pi - {{\sqrt 3 } \over 2} + 2$

d) Áp dụng quy tắc 2.

$\,y$ $\,y' = 2\sin x + 2\sin 2x = 2\sin x\left( {1 + 2\cos x} \right);y' = 0 \Leftrightarrow \left[ \matrix{ \sin x = 0 \hfill \cr \cos x = - {1 \over 2} \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = k\pi \hfill \cr x = \pm {{2\pi } \over 3} + 2k\pi ,k \in {\mathbb{Z}} \hfill \cr} \right.$

$y'' = 2\cos x + y''\left( {k\pi } \right) = 2\cos k\pi + 4\cos 2k\pi = 2\cos k\pi + k \in {\mathbb{Z}}$

Do đó hàm số đã cho đạt cực tiểu tại các điểm $x = k\pi$ $x = k\pi$, giá trị cực tiểu:

$y\left( {k\pi } \right) = 3 - 2\cos k\pi - \cos 2k\pi = 2 - 2\cos k\pi$ $y\left( {k\pi } \right) = 3 - 2\cos k\pi - \cos 2k\pi = 2 - 2\cos k\pi$

$y''\left( { \pm {{2\pi } \over 3} + k2\pi } \right) = 2\cos {{2\pi } \over 3} + 4\cos {{4\pi } \over 3} = 6\cos {{2\pi } \over 3} = - 3 < 0.$

Do đó hàm số đã cho đạt cực đại tại các điểm $x = \pm {{2\pi } \over 3} + k2\pi ,k \in {\mathbb{Z}}$ $x = \pm {{2\pi } \over 3} + k2\pi ,k \in {\mathbb{Z}}$; giá trị cực đại:

$y\left( { \pm {{2\pi } \over 3} + k2\pi } \right) = 3 - 2\cos {{2\pi } \over 3} - \cos {{4\pi } \over 3} = {9 \over 2}$ $y\left( { \pm {{2\pi } \over 3} + k2\pi } \right) = 3 - 2\cos {{2\pi } \over 3} - \cos {{4\pi } \over 3} = {9 \over 2}$

Bài 13 sgk trang 17 Toán Nâng cao 12 Đại số và Giải tích

Tìm các hệ số a, b, c, d của hàm số: $f\left( x \right) = a{x^3} + b{x^2} + cx + d$ $f\left( x \right) = a{x^3} + b{x^2} + cx + d$sao cho hàm số $f$ đạt cực tiểu tại điểm $x = 0,f\left( 0 \right) = 0$ $x = 0,f\left( 0 \right) = 0$ và đạt cực đại tại điểm $x = 1,f\left( 1 \right) = 1.$ $x = 1,f\left( 1 \right) = 1.$

Giải

Ta có: $f'\left( x \right) = 3a{x^2} + 2bx + c$

f đạt cực tiểu tại điểm x=0 nên $f'\left( 0 \right) = 0 \Rightarrow c = 0$

$f\left( 0 \right) = 0 \Rightarrow d = 0$ $f\left( 0 \right) = 0 \Rightarrow d = 0$. Vậy $f\left( x \right) = a{x^3} + b{x^2}$ $f\left( x \right) = a{x^3} + b{x^2}$

f đạt cực đại tại điểm x=1 nên $f'\left( 1 \right) = 0 \Rightarrow 3a + 2b = 0$

$f\left( 1 \right) = 1 \Rightarrow a + b = 1$ $f\left( 1 \right) = 1 \Rightarrow a + b = 1$

Ta có hệ phương trình:

$\left\{ \matrix{ 3a + 2b = 0 \hfill \cr a + b = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a = - 2 \hfill \cr b = 3 \hfill \cr} \right.$ $\left\{ \matrix{ 3a + 2b = 0 \hfill \cr a + b = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a = - 2 \hfill \cr b = 3 \hfill \cr} \right.$

Thử lại với $a=-2, b=3, c=d=0$ ta được:

$f\left( x \right) = - 2{x^3} + 3{x^2};\,\,\,\,\,\,\,f$ $f\left( x \right) = - 2{x^3} + 3{x^2};\,\,\,\,\,\,\,f'\left( x \right) = - 6{x^2} + 6x;\,\,\,\,\,\,f''\left( x \right) = - 12x + 6$

$f''\left( 0 \right) = 6 > 0 : Hàm số đạt cực tiểu tại điểm x=0; f\left( 0 \right) = 0;f''\left( 1 \right) = - 6 < 0$

Hàm số đạt cực đại tại điểm $x = 1;f\left( 1 \right) = 1$ $x = 1;f\left( 1 \right) = 1$

Vậy $a = - 2;b = 3;c = d = 0$

Bài 14 sgk trang 17 Toán Nâng cao 12 Đại số và Giải tích

Xác định các hệ số $a,b, c$ sao cho hàm số $f\left( x \right) = {x^3} + a{x^2} + bx + c$ $f\left( x \right) = {x^3} + a{x^2} + bx + c$đạt cực trị bằng 0 tại điểm x=-2 và đồ thị của hàm số đi qua điểm $A\left( {1;0} \right)$ $A\left( {1;0} \right)$

Giải

$f'\left( x \right) = 3{x^2} + 2ax + b$ f đạt cực trị tại điểm x=-2 nên $f'\left( { - 2} \right) = 0$

$\Rightarrow \,12 - 4a + b = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)f\left( { - 2} \right) = 0 \Rightarrow - 8 + 4a - 2b + c = 0\,\,\,\,\left( 2 \right)$ $\Rightarrow \,12 - 4a + b = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)f\left( { - 2} \right) = 0 \Rightarrow - 8 + 4a - 2b + c = 0\,\,\,\,\left( 2 \right)$

Đồ thị hàm số đi qua điểm $A\left( {1;0} \right)$ $A\left( {1;0} \right)$nên: $(f\left( 1 \right) = 0 \Rightarrow 1 + a + b + c = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)$ $(f\left( 1 \right) = 0 \Rightarrow 1 + a + b + c = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)$

Từ (1), (2), (3) ta có hệ phương trình:

$\left\{ \matrix{ 4a - b = 12 \hfill \cr 4a - 2b + c = 8 \hfill \cr a + b + c = - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a = 3 \hfill \cr b = 0 \hfill \cr c = - 4 \hfill \cr} \right.$ $\left\{ \matrix{ 4a - b = 12 \hfill \cr 4a - 2b + c = 8 \hfill \cr a + b + c = - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ a = 3 \hfill \cr b = 0 \hfill \cr c = - 4 \hfill \cr} \right.$

Vậy $a=3, b=0, c=-4$

Bài 15 sgk trang 17 Toán Nâng cao 12 Đại số và Giải tích

Chứng minh rằng với mọi giá trị của m, hàm số: $y = {{{x^2} - m\left( {m + 1} \right)x + {m^3} + 1} \over {x - m}}$ $y = {{{x^2} - m\left( {m + 1} \right)x + {m^3} + 1} \over {x - m}}$ luôn có cực đại và cực tiểu

Giải

TXĐ: $D = {\mathbb{R}}\backslash \left\{ m \right\}$ $D = {\mathbb{R}}\backslash \left\{ m \right\}$

$\eqalign{ & y$ $\eqalign{ & y' = {{\left[ {2x - m\left( {m + 1} \right)} \right]\left( {x - m} \right) - \left[ {{x^2} - m\left( {m + 1} \right)x + {m^3} + 1} \right]} \over {{{\left( {x - m} \right)}^2}}} \cr & \,\,\,\,\, = {{{x^2} - 2mx + {m^2} - 1} \over {{{\left( {x - m} \right)}^2}}},x \ne m \cr}$

$\eqalign{ & y$ $\eqalign{ & y' = 0 \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0 \Leftrightarrow {\left( {x - m} \right)^2} = 1 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \left[ \matrix{ x = m - 1;f\left( {m - 1} \right) = - {m^2} + m - 2 \hfill \cr x = m + 1;f\left( {m + 1} \right) = - {m^2} + m + 2 \hfill \cr} \right. \cr}$

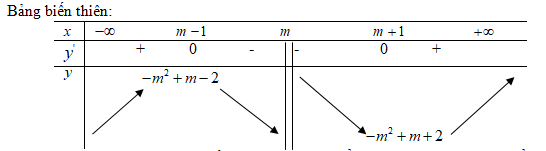
Giải bài tập sgk Toán Nâng cao bài 15

Với mọi giá trị của m, hàm số đạt cực đại tại điểm $x=m-1$ và đạt cực tiểu tại điểm x= m+1

Đây là tài liệu hỗ trợ các em trong quá trình ôn luyện kiến thức môn Toán 12 , giúp các em củng cố bài học và làm quen với các dạng bài tập cơ bản. Tài liệu cung cấp lời giải chi tiết để các em làm bài hiệu quả hơn, phục vụ các em trang bị kiến thức để bước vào các kì thi.

VnDoc xin giới thiệu tới các em giải bài tập sgk Toán 12 nâng cao bài 2. Hi vọng đây sẽ là tài liệu hữu ích giúp các em tự học. Để đạt kết quả cao hơn các em có thể tham khảo các tài liệu khác tại mục Tài liệu học tập lớp 12 mà VnDoc đã tổng hợp và đăng tải như: Trắc nghiệm Tiếng Anh 12, Trắc nghiệm Hóa học 12,...

Chia sẻ, đánh giá bài viết

1

566

Bài trước

Bài sau