Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải bài tập sgk Toán 12 Nâng cao Chương 1 bài 5: Đường tiệm cận của đồ thị hàm số

Giải sgk Toán 12 Nâng cao trang 35, 36

Bài trước

Bài sau

Giải bài tập Toán 12 Nâng cao bài 5 Đại số và Giải tích là tài liệu để các em tham khảo lời giải các bài tập trong sách giáo khoa Toán 12 Nâng cao. Tài liệu hướng dẫn các em làm bài cụ thể về Đường tiệm cận của đồ thị hàm số.

Giải bài tập SGK Toán 12 Nâng cao bài 5

Bài 34 trang 35 sgk Toán 12 Nâng cao Đại số và Giải tích
Bài 35 trang 35 sgk Toán 12 Nâng cao Đại số và Giải tích
Bài 36 trang 35 sgk Toán 12 Nâng cao Đại số và Giải tích
Bài 37 trang 36 sgk Toán 12 Nâng cao Đại số và Giải tích
Bài 38 trang 36 sgk Toán 12 Nâng cao Đại số và Giải tích
Bài 39 trang 36 sgk Toán 12 Nâng cao Đại số và Giải tích

Bài 34 trang 35 sgk Toán 12 Nâng cao Đại số và Giải tích

Tìm các đường tiệm cận của đồ thị hàm số sau:

a) $y = {{x - 2} \over {3x + 2}}$ $y = {{x - 2} \over {3x + 2}}$

b) $y = {{ - 2x - 2} \over {x + 3}}$ $y = {{ - 2x - 2} \over {x + 3}}$

c) $y = x + 2 - {1 \over {x - 3}}$ $y = x + 2 - {1 \over {x - 3}}$

d) $y = {{{x^2} - 3x + 4} \over {2x + 1}}$ $y = {{{x^2} - 3x + 4} \over {2x + 1}}$

e) $y = {{x + 2} \over {{x^2} - 1}}$ $y = {{x + 2} \over {{x^2} - 1}}$

f) $y = {x \over {{x^3} + 1}}$ $y = {x \over {{x^3} + 1}}$

Giải

a) TXĐ: $D = \mathbb R\backslash \left\{ { - {2 \over 3}} \right\}$ $D = \mathbb R\backslash \left\{ { - {2 \over 3}} \right\}$
Vì $\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{x + 2} \over {3x + 2}} = \mathop {\lim }\limits_{x \to + \infty } {{1 - {2 \over x}} \over {3 + {2 \over x}}} = {1 \over 3} và \mathop {\lim }\limits_{x \to - \infty } y = {1 \over 3} nên đường thẳng y = {1 \over 3}$ $\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{x + 2} \over {3x + 2}} = \mathop {\lim }\limits_{x \to + \infty } {{1 - {2 \over x}} \over {3 + {2 \over x}}} = {1 \over 3} và \mathop {\lim }\limits_{x \to - \infty } y = {1 \over 3} nên đường thẳng y = {1 \over 3}$là đường tiệm cận ngang của đồ thị.
Vì $\mathop {\lim }\limits_{x \to {{\left( { - {2 \over 3}} \right)}^ + }} y = - \infty\mathop {\lim }\limits_{x \to {{\left( { - {2 \over 3}} \right)}^ - }} y = + \infty ;$ $\mathop {\lim }\limits_{x \to {{\left( { - {2 \over 3}} \right)}^ + }} y = - \infty\mathop {\lim }\limits_{x \to {{\left( { - {2 \over 3}} \right)}^ - }} y = + \infty ;$ nên đường thẳng $x = - {2 \over 3}$ $x = - {2 \over 3}$là tiệm cận đứng của đồ thị.
b) TXĐ: $D =\mathbb R\backslash \left\{ { - 3} \right\}$ $D =\mathbb R\backslash \left\{ { - 3} \right\}$
Vì $\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{ - 2 - {2 \over x}} \over {1 + {3 \over x}}} = - 2 và \mathop {\lim }\limits_{x \to - \infty } y = - 2$ $\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{ - 2 - {2 \over x}} \over {1 + {3 \over x}}} = - 2 và \mathop {\lim }\limits_{x \to - \infty } y = - 2$ nên đường thẳng $y = - 2$ là tiệm cận ngang của đồ thị.
Vì $\mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ + }} y = + \infty và \mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} y = - \infty$ $\mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ + }} y = + \infty và \mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} y = - \infty$ nên đường thẳng $x = - 3$ là tiệm cận đứng của đồ thị.
c) TXĐ: $D =\mathbb R\backslash \left\{ 3 \right\}$ $D =\mathbb R\backslash \left\{ 3 \right\}$
Vì $\mathop {\lim }\limits_{x \to {3^ + }} y = - \infty và \mathop {\lim }\limits_{x \to {3^ - }} y = + \infty$ $\mathop {\lim }\limits_{x \to {3^ + }} y = - \infty và \mathop {\lim }\limits_{x \to {3^ - }} y = + \infty$ nên đường thẳng X=3 là tiệm cận đứng của đồ thị.
Ta có:

$\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x + 2} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } {{ - 1} \over {x - 3}} = 0 và \mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x + 2} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } {{ - 1} \over {x - 3}} = 0 nên đường thẳng y = x + 2$ $\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x + 2} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } {{ - 1} \over {x - 3}} = 0 và \mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x + 2} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } {{ - 1} \over {x - 3}} = 0 nên đường thẳng y = x + 2$ là tiệm cận xiên của đồ thị.
d) TXĐ: $D =\mathbb R\backslash \left\{ { - {1 \over 2}} \right\}$ $D =\mathbb R\backslash \left\{ { - {1 \over 2}} \right\}$
Vì $\mathop {\lim }\limits_{x \to {{\left( { - {1 \over 2}} \right)}^ + }} y = + \infty và \mathop {\lim }\limits_{x \to {{\left( { - {1 \over 2}} \right)}^ - }} y = - \infty nên đường thẳng x = - {1 \over 2} là$ $\mathop {\lim }\limits_{x \to {{\left( { - {1 \over 2}} \right)}^ + }} y = + \infty và \mathop {\lim }\limits_{x \to {{\left( { - {1 \over 2}} \right)}^ - }} y = - \infty nên đường thẳng x = - {1 \over 2} là$ tiệm cận đứng của đồ thị.

Tiệm cận xiên có dạng $y = ax + b$

$\eqalign{ & a = \mathop {\lim }\limits_{x \to \pm \infty } {y \over x} = \mathop {\lim }\limits_{x \to \pm \infty } {{{x^2} - 3x + 4} \over {x\left( {2x + 1} \right)}} = {1 \over 2} \cr & b = \mathop {\lim }\limits_{x \to \pm \infty } \left( {y - {x \over 2}} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{{{x^2} - 3x + 4} \over {2x + 1}} - {x \over 2}} \right) = \mathop {\lim }\limits_{x \to \pm \infty } {{ - 7x + 8} \over {2\left( {2x + 1} \right)}} = - {7 \over 4} \cr} \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty$ $\eqalign{ & a = \mathop {\lim }\limits_{x \to \pm \infty } {y \over x} = \mathop {\lim }\limits_{x \to \pm \infty } {{{x^2} - 3x + 4} \over {x\left( {2x + 1} \right)}} = {1 \over 2} \cr & b = \mathop {\lim }\limits_{x \to \pm \infty } \left( {y - {x \over 2}} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{{{x^2} - 3x + 4} \over {2x + 1}} - {x \over 2}} \right) = \mathop {\lim }\limits_{x \to \pm \infty } {{ - 7x + 8} \over {2\left( {2x + 1} \right)}} = - {7 \over 4} \cr} \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty$

Đường thẳng $y = {x \over 2} - {7 \over 4}$ $y = {x \over 2} - {7 \over 4}$là tiệm cận xiên của đồ thị (khi $x \to + \infty và x \to - \infty$ $x \to + \infty và x \to - \infty$).

Cách khác:

Ta có: $y = {1 \over 2}.{{{x^2} - 3x + 4} \over {x + {1 \over 2}}} = {1 \over 2}\left( {x - {7 \over 2} + {{23} \over {4\left( {x + {1 \over 2}} \right)}}} \right)$ $y = {1 \over 2}.{{{x^2} - 3x + 4} \over {x + {1 \over 2}}} = {1 \over 2}\left( {x - {7 \over 2} + {{23} \over {4\left( {x + {1 \over 2}} \right)}}} \right)$

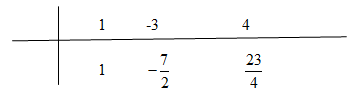
Giải bài tập Toán Nâng cao 12 bài 34
Vì $\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {{x \over 2} - {7 \over 4}} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {{23} \over {8\left( {x + {1 \over 2}} \right)}} = 0$ $\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {{x \over 2} - {7 \over 4}} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {{23} \over {8\left( {x + {1 \over 2}} \right)}} = 0$nên đường thẳng $y = {x \over 2} - {7 \over 4}$ $y = {x \over 2} - {7 \over 4}$ là tiệm cận xiên của đồ thị.

e) TXĐ: $D =\mathbb R\backslash \left\{ { - 1;1} \right\}$ $D =\mathbb R\backslash \left\{ { - 1;1} \right\}$
Vì $\mathop {\lim }\limits_{x \to \pm \infty } y = 0$ $\mathop {\lim }\limits_{x \to \pm \infty } y = 0$ nên đường thẳng y = 0 là tiệm cận ngang của đồ thị. $\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = + \infty và \mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = - \infty$ $\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = + \infty và \mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = - \infty$ nên đường thẳng x = 1 là tiệm cận đứng của đồ thị.

$\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = - \infty và \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = + \infty$ $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = - \infty và \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = + \infty$nên đường thẳng $x = - 1$ là tiệm cận đứng của đồ thị.

f) TXĐ: $D =\mathbb R\backslash \left\{ { - 1} \right\}$ $D =\mathbb R\backslash \left\{ { - 1} \right\}$
Vì $\mathop {\lim }\limits_{x \to \pm \infty } y = 0$ $\mathop {\lim }\limits_{x \to \pm \infty } y = 0$nên y=0 là tiệm cận ngang

$\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = - \infty$ $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = - \infty$ và \ $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty$ $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty$ nên x= -1 là tiệm cận đứng.

Bài 35 trang 35 sgk Toán 12 Nâng cao Đại số và Giải tích

Tìm các tiệm cận của đồ thị hàm số sau:
(a) $\,y = {{2x - 1} \over {{x^2}}} + x - 3\,;$ $\,y = {{2x - 1} \over {{x^2}}} + x - 3\,;$

(b) $\,\,{{{x^3} + 2} \over {{x^2} - 2x}}$ $\,\,{{{x^3} + 2} \over {{x^2} - 2x}}$

(d) $\,\,{{{x^2} + x + 1} \over { - 5{x^2} - 2x + 3}}$ $\,\,{{{x^2} + x + 1} \over { - 5{x^2} - 2x + 3}}$

Giải

a) TXĐ: $D =\mathbb R\backslash \left\{ 0 \right\}$ $D =\mathbb R\backslash \left\{ 0 \right\}$
Vì $\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ - }} y = - \infty$ $\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ - }} y = - \infty$ nên x = 0 là tiệm cận đứng.

$\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 3} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {{2x - 1} \over {{x^2}}} = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{2 \over x} - {1 \over {{x^2}}}} \right) = 0 nên y = x – 3$ $\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 3} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {{2x - 1} \over {{x^2}}} = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{2 \over x} - {1 \over {{x^2}}}} \right) = 0 nên y = x – 3$ là tiệm cận xiên.
b) TXĐ: $D =\mathbb R\backslash \left\{ {0;2} \right\}$ $D =\mathbb R\backslash \left\{ {0;2} \right\}$
$\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} {{{x^3} + 2} \over {x\left( {x - 2} \right)}} = - \infty và(\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ + }} {{{x^3} + 2} \over {x\left( {x - 2} \right)}} = + \infty$ $\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} {{{x^3} + 2} \over {x\left( {x - 2} \right)}} = - \infty và(\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ + }} {{{x^3} + 2} \over {x\left( {x - 2} \right)}} = + \infty$nên x = 0 là tiệm cận đứng.
$\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} {{{x^3} + 2} \over {x\left( {x - 2} \right)}} = + \infty và \mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} {{{x^3} + 2} \over {x\left( {x - 2} \right)}} = - \infty$ $\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} {{{x^3} + 2} \over {x\left( {x - 2} \right)}} = + \infty và \mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} {{{x^3} + 2} \over {x\left( {x - 2} \right)}} = - \infty$ nên x=2 là tiệm cận đứng.

Tiệm cận xiên có dạng $y = ax +b$

$\eqalign{ & a = \mathop {\lim }\limits_{x \to \pm \infty } {y \over x} = \mathop {\lim }\limits_{x \to \pm \infty } {{{x^3} + 2} \over {{x^3} - 2{x^2}}} = \mathop {\lim }\limits_{x \to \pm \infty } {{1 + {2 \over {{x^3}}}} \over {1 - {2 \over x}}} = 1 \cr & b = \mathop {\lim }\limits_{x \to \pm \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{{{x^3} + 2} \over {{x^2} - 2x}} - x} \right) = \mathop {\lim }\limits_{x \to \pm \infty } {{2{x^2} + 2} \over {{x^2} - 2x}} = 2 \cr}$ $\eqalign{ & a = \mathop {\lim }\limits_{x \to \pm \infty } {y \over x} = \mathop {\lim }\limits_{x \to \pm \infty } {{{x^3} + 2} \over {{x^3} - 2{x^2}}} = \mathop {\lim }\limits_{x \to \pm \infty } {{1 + {2 \over {{x^3}}}} \over {1 - {2 \over x}}} = 1 \cr & b = \mathop {\lim }\limits_{x \to \pm \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{{{x^3} + 2} \over {{x^2} - 2x}} - x} \right) = \mathop {\lim }\limits_{x \to \pm \infty } {{2{x^2} + 2} \over {{x^2} - 2x}} = 2 \cr}$

Đường thẳng $y = x + 2$ là tiệm cận xiên của đồ thị.

c) TXĐ: $D =\mathbb R\backslash \left\{ { - 1;1} \right\}$ $D =\mathbb R\backslash \left\{ { - 1;1} \right\}$
$\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} {{{x^3} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = + \infty và \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} {{{x^3} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = - \infty$ $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} {{{x^3} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = + \infty và \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} {{{x^3} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = - \infty$nên x=-1 là tiệm cận đứng.
$\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} {{{x^3} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = - \infty và \mathop {\lim }\limits_{x \to {1^ - }} y = - \infty nên x = 1$ $\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} {{{x^3} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = - \infty và \mathop {\lim }\limits_{x \to {1^ - }} y = - \infty nên x = 1$ là tiệm cận đứng.

Tiệm cận xiên có dạng $y = ax + b$

$\eqalign{ & a = \mathop {\lim }\limits_{x \to \pm \infty } {y \over x} = \mathop {\lim }\limits_{x \to \pm \infty } {{{x^3} + x + 1} \over {x\left( {{x^2} - 1} \right)}} = \mathop {\lim }\limits_{x \to \pm \infty } {{1 + {1 \over {{x^2}}} + {1 \over {{x^3}}}} \over {1 - {1 \over {{x^2}}}}} = 1 \cr & b = \mathop {\lim }\limits_{x \to \pm \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{{{x^3} + x + 1} \over {{x^2} - 1}}} \right) = \mathop {\lim }\limits_{x \to \pm \infty } {{2x + 1} \over {{x^2} - 1}} = 0 \cr}$ $\eqalign{ & a = \mathop {\lim }\limits_{x \to \pm \infty } {y \over x} = \mathop {\lim }\limits_{x \to \pm \infty } {{{x^3} + x + 1} \over {x\left( {{x^2} - 1} \right)}} = \mathop {\lim }\limits_{x \to \pm \infty } {{1 + {1 \over {{x^2}}} + {1 \over {{x^3}}}} \over {1 - {1 \over {{x^2}}}}} = 1 \cr & b = \mathop {\lim }\limits_{x \to \pm \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{{{x^3} + x + 1} \over {{x^2} - 1}}} \right) = \mathop {\lim }\limits_{x \to \pm \infty } {{2x + 1} \over {{x^2} - 1}} = 0 \cr}$

$\Rightarrow y = x$ $\Rightarrow y = x$ là tiệm cận xiên.
d) TXĐ: $D =\mathbb R\backslash \left\{ { - 1;{3 \over 5}} \right\}$ $D =\mathbb R\backslash \left\{ { - 1;{3 \over 5}} \right\}$
$Vì \mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } {{1 + {1 \over x} + {1 \over {{x^2}}}} \over { - 5 - {2 \over x} + {3 \over {{x^2}}}}} = - {1 \over 5}$ $Vì \mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } {{1 + {1 \over x} + {1 \over {{x^2}}}} \over { - 5 - {2 \over x} + {3 \over {{x^2}}}}} = - {1 \over 5}$nên $y = - {1 \over 5}$ $y = - {1 \over 5}$ là tiệm cận ngang.
$\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} {{{x^2} + x + 1} \over {\left( {x + 1} \right)\left( {3 - 5x} \right)}} = + \infty và \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = - \infty nên x = -1$ $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} {{{x^2} + x + 1} \over {\left( {x + 1} \right)\left( {3 - 5x} \right)}} = + \infty và \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = - \infty nên x = -1$ là tiệm cận đứng.
$\mathop {\lim }\limits_{x \to {{\left( {{3 \over 5}} \right)}^ + }} y = \mathop {\lim }\limits_{x \to {{\left( {{3 \over 5}} \right)}^ + }} {{{x^2} + x + 1} \over {\left( {x + 1} \right)\left( {3 - 5x} \right)}} = - \infty và \mathop {\lim }\limits_{x \to {{\left( {{3 \over 5}} \right)}^ - }} y = \mathop {\lim }\limits_{x \to {{\left( {{3 \over 5}} \right)}^ - }} {{{x^2} + x + 1} \over {\left( {x + 1} \right)\left( {3 - 5x} \right)}} = + \infty$ $\mathop {\lim }\limits_{x \to {{\left( {{3 \over 5}} \right)}^ + }} y = \mathop {\lim }\limits_{x \to {{\left( {{3 \over 5}} \right)}^ + }} {{{x^2} + x + 1} \over {\left( {x + 1} \right)\left( {3 - 5x} \right)}} = - \infty và \mathop {\lim }\limits_{x \to {{\left( {{3 \over 5}} \right)}^ - }} y = \mathop {\lim }\limits_{x \to {{\left( {{3 \over 5}} \right)}^ - }} {{{x^2} + x + 1} \over {\left( {x + 1} \right)\left( {3 - 5x} \right)}} = + \infty$nên $x = {3 \over 5}$ $x = {3 \over 5}$ là tiệm cận đứng.

Bài 36 trang 35 sgk Toán 12 Nâng cao Đại số và Giải tích

Tìm các tiệm cận của đồ thị hàm số sau:

(a) $\,\,y = \sqrt {{x^2} - 1} \,\,$ $\,\,y = \sqrt {{x^2} - 1} \,\,$

b) $y = 2x + \sqrt {{x^2} - 1}$ $y = 2x + \sqrt {{x^2} - 1}$

c) $y = x + \sqrt {{x^2} + 1}$ $y = x + \sqrt {{x^2} + 1}$

d) $y = \sqrt {{x^2} + x + 1}$ $y = \sqrt {{x^2} + x + 1}$

Giải

a) TXĐ: $D =\mathbb R\backslash ( - \infty ;1{\rm{]}} \cup {\rm{[}}1; + \infty )$ $D =\mathbb R\backslash ( - \infty ;1{\rm{]}} \cup {\rm{[}}1; + \infty )$

Tiệm cận xiên khi $x \to + \infty$ $x \to + \infty$

$a = \mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} - 1} } \over x} = \mathop {\lim }\limits_{x \to + \infty } {{x\sqrt {1 - {1 \over {{x^2}}}} } \over x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 - {1 \over {{x^2}}}} = 1b = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 1} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {{ - 1} \over {\sqrt {{x^2} - 1} + x}} = 0$ $a = \mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} - 1} } \over x} = \mathop {\lim }\limits_{x \to + \infty } {{x\sqrt {1 - {1 \over {{x^2}}}} } \over x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 - {1 \over {{x^2}}}} = 1b = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 1} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {{ - 1} \over {\sqrt {{x^2} - 1} + x}} = 0$

Vậy đường thẳng y = x là tiệm cận xiên của đồ thị khi $x \to + \infty$ $x \to + \infty$

Tiệm cận xiên khi $x \to - \infty$ $x \to - \infty$
$a = \mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^2} - 1} } \over x} = \mathop {\lim }\limits_{x \to - \infty } {{ - x\sqrt {1 - {1 \over {{x^2}}}} } \over x} = - \mathop {\lim }\limits_{x \to - \infty } \sqrt {1 - {1 \over {{x^2}}}} = - b = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 1} - x} \right) = \mathop {\lim }\limits_{x \to - \infty } {{ - 1} \over {\sqrt {{x^2} - 1} + x}} = 0$ $a = \mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^2} - 1} } \over x} = \mathop {\lim }\limits_{x \to - \infty } {{ - x\sqrt {1 - {1 \over {{x^2}}}} } \over x} = - \mathop {\lim }\limits_{x \to - \infty } \sqrt {1 - {1 \over {{x^2}}}} = - b = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 1} - x} \right) = \mathop {\lim }\limits_{x \to - \infty } {{ - 1} \over {\sqrt {{x^2} - 1} + x}} = 0$

Vậy đường thẳng y = -x là tiệm cận xiên của đồ thị (khi $x \to - \infty$ $x \to - \infty$).

b) TXĐ: $D =\mathbb R\backslash ( - \infty ;1{\rm{]}} \cup {\rm{[}}1; + \infty )$ $D =\mathbb R\backslash ( - \infty ;1{\rm{]}} \cup {\rm{[}}1; + \infty )$

Tiệm cận xiên khi $x \to + \infty$ $x \to + \infty$
$b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - 3x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 1} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {{ - 1} \over {\sqrt {{x^2} - 1} + x}} = 0$ $b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - 3x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 1} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {{ - 1} \over {\sqrt {{x^2} - 1} + x}} = 0$
Vậy đường thẳng $y = 3x$ là tiệm cận xiên của đồ thị ( $khi x \to + \infty$ $khi x \to + \infty$).

Tiệm cận xiên khi $x \to - \infty$ $x \to - \infty$
$a = \mathop {\lim }\limits_{x \to - \infty } {y \over x} = \mathop {\lim }\limits_{x \to - \infty } \left( {2 + {{\sqrt {{x^2} + 1} } \over x}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {2 - \sqrt {1 - {1 \over {{x^2}}}} } \right) = 1$ $a = \mathop {\lim }\limits_{x \to - \infty } {y \over x} = \mathop {\lim }\limits_{x \to - \infty } \left( {2 + {{\sqrt {{x^2} + 1} } \over x}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {2 - \sqrt {1 - {1 \over {{x^2}}}} } \right) = 1$
$b = \mathop {\lim }\limits_{x \to - \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 1} + x} \right) = \mathop {\lim }\limits_{x \to - \infty } {{ - 1} \over {\sqrt {{x^2} - 1} - x}} = 0$ $b = \mathop {\lim }\limits_{x \to - \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 1} + x} \right) = \mathop {\lim }\limits_{x \to - \infty } {{ - 1} \over {\sqrt {{x^2} - 1} - x}} = 0$
Vậy đường thẳng y = x là tiệm cận xiên của đồ thị (khi $x \to - \infty$ $x \to - \infty$)

c) TXĐ: $D =\mathbb R$ $D =\mathbb R$

Tiệm cận xiên khi $x \to + \infty$ $x \to + \infty$

$\eqalign{ & a = \mathop {\lim }\limits_{x \to + \infty } {y \over x} = \mathop {\lim }\limits_{x \to + \infty } \left( {1 + {{\sqrt {{x^2} + 1} } \over x}} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {1 + \sqrt {1 + {1 \over {{x^2}}}} } \right) = 2 \cr & b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - 2x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 1} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {1 \over {\sqrt {{x^2} + 1} + x}} = 0 \cr}$ $\eqalign{ & a = \mathop {\lim }\limits_{x \to + \infty } {y \over x} = \mathop {\lim }\limits_{x \to + \infty } \left( {1 + {{\sqrt {{x^2} + 1} } \over x}} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {1 + \sqrt {1 + {1 \over {{x^2}}}} } \right) = 2 \cr & b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - 2x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 1} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {1 \over {\sqrt {{x^2} + 1} + x}} = 0 \cr}$

Đường thẳng $y = 2x$ là tiệm cận xiên (khi $x \to + \infty$ $x \to + \infty$)

Tiệm cận khi $x \to - \infty$ $x \to - \infty$
$\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {x + \sqrt {{x^2} - 1} } \right) = \mathop {\lim }\limits_{x \to - \infty } {1 \over {x - \sqrt {{x^2} - 1} }} = 0$ $\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {x + \sqrt {{x^2} - 1} } \right) = \mathop {\lim }\limits_{x \to - \infty } {1 \over {x - \sqrt {{x^2} - 1} }} = 0$
Đường thẳng y = 0 là tiệm cận ngang (khi $x \to - \infty$ $x \to - \infty$)

d) TXĐ: $D =\mathbb R$ $D =\mathbb R$
$a = \mathop {\lim }\limits_{x \to + \infty } {y \over x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 + {1 \over x} + {1 \over {{x^2}}}} = 1$ $a = \mathop {\lim }\limits_{x \to + \infty } {y \over x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 + {1 \over x} + {1 \over {{x^2}}}} = 1$

$\eqalign{ & b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 1} - x} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to + \infty } {{x + 1} \over {\sqrt {{x^2} + x + 1} + x}} = \mathop {\lim }\limits_{x \to + \infty } {{1 + {1 \over x}} \over {\sqrt {1 + {1 \over x} + {1 \over {{x^2}}}} }+1} = {1 \over 2} \cr}$ $\eqalign{ & b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 1} - x} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to + \infty } {{x + 1} \over {\sqrt {{x^2} + x + 1} + x}} = \mathop {\lim }\limits_{x \to + \infty } {{1 + {1 \over x}} \over {\sqrt {1 + {1 \over x} + {1 \over {{x^2}}}} }+1} = {1 \over 2} \cr}$

Đường thẳng $y = x + {1 \over 2}$ $y = x + {1 \over 2}$ là tiệm cận xiên (khi $x \to + \infty$ $x \to + \infty$)
$a = \mathop {\lim }\limits_{x \to - \infty } {y \over x} = \mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^2} + x + 1} } \over x} = \mathop {\lim }\limits_{x \to - \infty } {{ - x\sqrt {1 + {1 \over x} + {1 \over {{x^2}}}} } \over x} = \mathop {\lim }\limits_{x \to - \infty } -\sqrt {1 + {1 \over x} + {1 \over {{x^2}}}} = - 1$ $a = \mathop {\lim }\limits_{x \to - \infty } {y \over x} = \mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^2} + x + 1} } \over x} = \mathop {\lim }\limits_{x \to - \infty } {{ - x\sqrt {1 + {1 \over x} + {1 \over {{x^2}}}} } \over x} = \mathop {\lim }\limits_{x \to - \infty } -\sqrt {1 + {1 \over x} + {1 \over {{x^2}}}} = - 1$
$b = \mathop {\lim }\limits_{x \to - \infty } \left( {y + x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + x + 1} + x} \right) = \mathop {\lim }\limits_{x \to - \infty } {{x + 1} \over {\sqrt {{x^2} + x + 1} - x}} = \mathop {\lim }\limits_{x \to - \infty } {{1 + {1 \over x}} \over { - \sqrt {1 + {1 \over x} + {1 \over {{x^2}}}} }-1} = - {1 \over 2}$ $b = \mathop {\lim }\limits_{x \to - \infty } \left( {y + x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + x + 1} + x} \right) = \mathop {\lim }\limits_{x \to - \infty } {{x + 1} \over {\sqrt {{x^2} + x + 1} - x}} = \mathop {\lim }\limits_{x \to - \infty } {{1 + {1 \over x}} \over { - \sqrt {1 + {1 \over x} + {1 \over {{x^2}}}} }-1} = - {1 \over 2}$
Đường thẳng $y = - x - {1 \over 2}$ $y = - x - {1 \over 2}$ là tiệm cận xiên (khi $x \to - \infty$ $x \to - \infty$)

Bài 37 trang 36 sgk Toán 12 Nâng cao Đại số và Giải tích

Tìm các đường tiệm cận của đồ thị mỗi hàm số sau:

a) $y = x + \sqrt {{x^2} - 1}$ $y = x + \sqrt {{x^2} - 1}$

b) $y = \sqrt {{x^2} - 4x + 3}$ $y = \sqrt {{x^2} - 4x + 3}$

c) $y = \sqrt {{x^2} + 4}$ $y = \sqrt {{x^2} + 4}$

d) $y = {{{x^2} + x + 1} \over {{x^2} - 1}}$ $y = {{{x^2} + x + 1} \over {{x^2} - 1}}$

Giải

a) TXĐ: $D = \left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)$ $D = \left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)$
$a = \mathop {\lim }\limits_{x \to + \infty } {y \over x} = \mathop {\lim }\limits_{x \to + \infty } \left( {1 + {{\sqrt {{x^2} - 1} } \over x}} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {1 + \sqrt {1 - {1 \over {{x^2}}}} } \right) = 2$ $a = \mathop {\lim }\limits_{x \to + \infty } {y \over x} = \mathop {\lim }\limits_{x \to + \infty } \left( {1 + {{\sqrt {{x^2} - 1} } \over x}} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {1 + \sqrt {1 - {1 \over {{x^2}}}} } \right) = 2$
$b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - 2x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 1} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {{ - 1} \over {\sqrt {{x^2} - 1} + x}} = 0$ $b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - 2x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 1} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {{ - 1} \over {\sqrt {{x^2} - 1} + x}} = 0$
Ta có tiệm cận xiên y = 2x (khi $x \to + \infty$ $x \to + \infty$)

$\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {x + \sqrt {{x^2} - 1} } \right) = \mathop {\lim }\limits_{x \to - \infty } {{ - 1} \over {\sqrt {{x^2} - 1} - x}} = 0$ $\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {x + \sqrt {{x^2} - 1} } \right) = \mathop {\lim }\limits_{x \to - \infty } {{ - 1} \over {\sqrt {{x^2} - 1} - x}} = 0$

Ta có tiệm cận ngang y = 0 (khi $x \to - \infty$ $x \to - \infty$)

b) TXĐ: $D = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)$ $D = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)$
$a = \mathop {\lim }\limits_{x \to + \infty } {y \over x} = \mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} - 4x + 3} } \over x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} = 1$ $a = \mathop {\lim }\limits_{x \to + \infty } {y \over x} = \mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} - 4x + 3} } \over x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} = 1$
$(b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 4x + 3} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {{ - 4x + 3} \over {\sqrt {{x^2} - 4x + 3} + x}} = \mathop {\lim }\limits_{x \to + \infty } {{ - 4 + {3 \over x}} \over {\sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} + 1}} = - 2$ $(b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 4x + 3} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {{ - 4x + 3} \over {\sqrt {{x^2} - 4x + 3} + x}} = \mathop {\lim }\limits_{x \to + \infty } {{ - 4 + {3 \over x}} \over {\sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} + 1}} = - 2$
Ta có tiệm cận xiên y = x -2 (khi $x \to + \infty$ $x \to + \infty$).
$a = \mathop {\lim }\limits_{x \to - \infty } {y \over x} = \mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^2} - 4x + 3} } \over x} = \mathop {\lim }\limits_{x \to - \infty } {{ - x\sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} } \over x} = - \mathop {\lim }\limits_{x \to - \infty } \sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} = - 1$ $a = \mathop {\lim }\limits_{x \to - \infty } {y \over x} = \mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^2} - 4x + 3} } \over x} = \mathop {\lim }\limits_{x \to - \infty } {{ - x\sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} } \over x} = - \mathop {\lim }\limits_{x \to - \infty } \sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} = - 1$

$\eqalign{ & b = \mathop {\lim }\limits_{x \to - \infty } \left( {y + x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 4x + 3} + x} \right) = \mathop {\lim }\limits_{x \to - \infty } {{ - 4x + 3} \over {\sqrt {{x^2} - 4x + 3} - x}} = \mathop {\lim }\limits_{x \to - \infty } {{ - 4x + 3} \over { - x\sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} - x}} \cr & \,\, = \,\,\,\mathop {\lim }\limits_{x \to - \infty } {{ - 4 + {3 \over x}} \over { - \sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} - 1}} = {{ - 4} \over { - 2}} = 2 \cr}$ $\eqalign{ & b = \mathop {\lim }\limits_{x \to - \infty } \left( {y + x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 4x + 3} + x} \right) = \mathop {\lim }\limits_{x \to - \infty } {{ - 4x + 3} \over {\sqrt {{x^2} - 4x + 3} - x}} = \mathop {\lim }\limits_{x \to - \infty } {{ - 4x + 3} \over { - x\sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} - x}} \cr & \,\, = \,\,\,\mathop {\lim }\limits_{x \to - \infty } {{ - 4 + {3 \over x}} \over { - \sqrt {1 - {4 \over x} + {3 \over {{x^2}}}} - 1}} = {{ - 4} \over { - 2}} = 2 \cr}$

Tiệm cận xiên:$y = -x + 2$ (khi $x \to - \infty$ $x \to - \infty$).

c) TXD: $D =\mathbb R$ $D =\mathbb R$

$a = \mathop {\lim }\limits_{x \to + \infty } {y \over x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 + {4 \over {{x^2}}}} = 1b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 4} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {4 \over {\sqrt {{x^2} + 4} + x}} = 0$ $a = \mathop {\lim }\limits_{x \to + \infty } {y \over x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 + {4 \over {{x^2}}}} = 1b = \mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 4} - x} \right) = \mathop {\lim }\limits_{x \to + \infty } {4 \over {\sqrt {{x^2} + 4} + x}} = 0$
Tiệm cận xiên y = x (khi $x \to + \infty$ $x \to + \infty$
$a = \mathop {\lim }\limits_{x \to - \infty } {y \over x} = \mathop {\lim }\limits_{x \to - \infty }- \sqrt {1 + {4 \over {{x^2}}}} = - 1b = \mathop {\lim }\limits_{x \to - \infty } \left( {y + x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 4} + x} \right) = \mathop {\lim }\limits_{x \to - \infty } {4 \over {\sqrt {{x^2} + 4} - x}} = 0$ $a = \mathop {\lim }\limits_{x \to - \infty } {y \over x} = \mathop {\lim }\limits_{x \to - \infty }- \sqrt {1 + {4 \over {{x^2}}}} = - 1b = \mathop {\lim }\limits_{x \to - \infty } \left( {y + x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 4} + x} \right) = \mathop {\lim }\limits_{x \to - \infty } {4 \over {\sqrt {{x^2} + 4} - x}} = 0$
Tiệm cận xiên y = -x (khi $x \to - \infty$ $x \to - \infty$

d) TXĐ: $D =\mathbb R\backslash \left\{ { - 1;1} \right\}$ $D =\mathbb R\backslash \left\{ { - 1;1} \right\}$
Vì $\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{1 + {1 \over x} + {1 \over {{x^2}}}} \over {1 - {1 \over {{x^2}}}}} = 1$ $\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{1 + {1 \over x} + {1 \over {{x^2}}}} \over {1 - {1 \over {{x^2}}}}} = 1$
Tiệm cận ngang: y = 1 (khi $(x \to - \infty và x \to + \infty$ $(x \to - \infty và x \to + \infty$)

$\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} {{{x^2} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = + \infty và \mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} {{{x^2} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = - \infty nên x = 1$ $\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} {{{x^2} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = + \infty và \mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} {{{x^2} + x + 1} \over {\left( {x - 1} \right)\left( {x + 1} \right)}} = - \infty nên x = 1$là tiệm cận đứng.

Tương tự: $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = - \infty và \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty$ $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = - \infty và \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty$ $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = - \infty$ $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = - \infty$và $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty$ $\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty$nên x = -1 là tiệm cận đứng.

Bài 38 trang 36 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Tìm tiệm cận đứng và tiệm cận xiên của đồ thị C của hàm số:

$y = {{{x^2} - 2x + 3} \over {x - 3}}$ $y = {{{x^2} - 2x + 3} \over {x - 3}}$

b) Xác định giao điểm I của hai tiệm cận trên và viết công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ $\overrightarrow {OI} .$ $\overrightarrow {OI} .$

c) Viết phương trinh của đường cong C đối với hệ tọa độ IXY

Từ đó suy ra rằng I là tâm đối xứng của đường cong C

Giải

a) Ta có: $y = x + 1 + {5 \over {x - 3}}$ $y = x + 1 + {5 \over {x - 3}}$

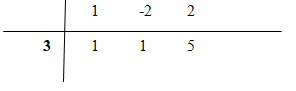
Giải bài tập Toán Nâng cao 12 bài 38 câu a

TXĐ: $D =\mathbb R\backslash \left\{ 3 \right\}$ $D =\mathbb R\backslash \left\{ 3 \right\}$

Vì

$\left\{ \matrix{ y$ $\left\{ \matrix{ y'\left( 1 \right) = 0 \hfill \cr y\left( 1 \right) = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ b = - 3 \hfill \cr c = 0 \hfill \cr} \right. \mathop {\lim }\limits_{x \to {3^ + }} y = + \infty và \mathop {\lim }\limits_{x \to {3^ - }} y = - \infty$nên x = 3 là tiệm cận đứng.

$\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {5 \over {x - 3}} = 0$ $\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {5 \over {x - 3}} = 0$nên y = x + 1 là tiệm cận xiên.

b) Tọa độ giao điểm I(x;y) của hai tiệm cận là nghiệm của hệ phương trình

$\left\{ \matrix{ x = 3 \hfill \cr y = x + 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = 3 \hfill \cr y = 4 \hfill \cr} \right.$ $\left\{ \matrix{ x = 3 \hfill \cr y = x + 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = 3 \hfill \cr y = 4 \hfill \cr} \right.$

Vậy I(3;4) là giao điểm của hai tiệm cận trên.

Công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ $\overrightarrow {OI}$ $\overrightarrow {OI}$ là

$\left\{ \matrix{ x = X + 3 \hfill \cr y = Y + 4 \hfill \cr} \right.$ $\left\{ \matrix{ x = X + 3 \hfill \cr y = Y + 4 \hfill \cr} \right.$

c) Phương trình của đường cong C đối với hệ tọa độ IXY là

$Y + 4 = X + 3 + 1 + {5 \over {X + 3 - 3}} \Leftrightarrow Y = X + {5 \over X}$ $Y + 4 = X + 3 + 1 + {5 \over {X + 3 - 3}} \Leftrightarrow Y = X + {5 \over X}$

Đây là hàm số lẻ, do đó C nhận gốc tọa độ I làm tâm đối xứng.

Bài 39 trang 36 sgk Toán 12 Nâng cao Đại số và Giải tích

Cùng các câu hỏi như trong bài tập 38 đối với đồ thị của hàm số sau:

a) $y = {{{x^2} + x - 4} \over {x + 2}}$ $y = {{{x^2} + x - 4} \over {x + 2}}$

b) $y = {{{x^2} - 8x + 19} \over {x - 5}}$ $y = {{{x^2} - 8x + 19} \over {x - 5}}$

Giải

a) $y = x - 1 - {2 \over {x + 2}}$ $y = x - 1 - {2 \over {x + 2}}$

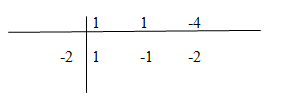
Giải bài tập Toán 12 Nâng cao bài 39 câu a

TXĐ: $D =\mathbb R\backslash \left\{ { - 2} \right\}$ $D =\mathbb R\backslash \left\{ { - 2} \right\}$

x=-2 là tiệm cận đứng.
$\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {{ - 2} \over {x + 2}}=0$ $\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {{ - 2} \over {x + 2}}=0$ nên y = x -1 là tiệm cận xiên.

b) Tọa độ giao điểm I của hai tiệm cận là nghiệm hệ

$\left\{ \matrix{ x = - 2 \hfill \cr y = x - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 2 \hfill \cr y = - 3 \hfill \cr} \right.$ $\left\{ \matrix{ x = - 2 \hfill \cr y = x - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - 2 \hfill \cr y = - 3 \hfill \cr} \right.$

Vậy I(-2;-3). Công thức chuyển hệ tọa độ trong phép tịnh tiến vé tơ $\overrightarrow {OI}$ $\overrightarrow {OI}$ là

$\left\{ \matrix{ x = X - 2 \hfill \cr y = Y - 3 \hfill \cr} \right.$ $\left\{ \matrix{ x = X - 2 \hfill \cr y = Y - 3 \hfill \cr} \right.$

c) Ta nói: $y = x - 3 + {4 \over {x - 5}}$ $y = x - 3 + {4 \over {x - 5}}$

Tiệm cận đứng: x = 5; tiệm cận xiên: y = x – 3

$I\left( {5;2} \right);\,\,\left\{ \matrix{ x = X + 5 \hfill \cr y = Y + 2 \hfill \cr} \right.$ $I\left( {5;2} \right);\,\,\left\{ \matrix{ x = X + 5 \hfill \cr y = Y + 2 \hfill \cr} \right.$

Phương trình của đường cong đối với hệ tọa độ IXY là $Y = X + {4 \over X}$ $Y = X + {4 \over X}$

Hi vọng đây sẽ là tài liệu hữu ích giúp các em củng cố kiến thức, nắm vững lí thuyết bài học và chuẩn bị thật tốt cho mình hành trang kiến thức để vượt qua những kì thi quan trọng. Để đạt hiệu quả cao các em xem thêm Giải bài tập Toán 12, Giải vở bài tập Toán 12, Trắc nghiệm Toán 12,...

VnDoc xin giới thiệu tới các em Giải bài tập Toán 12 nâng cao bài 5 Đại số và Giải tích. Các em có thể tham khảo thêm tài liệu của các môn học khác tại mục Tài liệu học tập lớp 12 do VnDoc tổng hợp và đăng tải như: Trắc nghiệm Hóa học 12, Trắc nghiệm Tiếng Anh 12, Trắc nghiệm Sinh học 12,...

Chia sẻ, đánh giá bài viết

239

Bài trước

Bài sau