Giải bài tập Toán 12 Nâng cao Chương 1 bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một hàm số đa thức

Giải bài tập sgk Toán Nâng cao 12 bài 6 Đại số và Giải tích là tài liệu hướng dẫn các em giải các bài tập trong sách giáo khoa Toán 12 Nâng cao. Tài liệu cung cấp chi tiết lời giải từng dạng bài tập phần Khảo sát sự biến thiên và vẽ đồ thị của một hàm số đa thức.

Bài 40 trang 43 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\)

b) Viết phương trình tiếp tuyến của đồ thị tại điểm uốn.

c) Chứng minh rằng điểm uốn là tâm đối xứng của đồ thị.

Giải

a) Tập xác đinh: \(D=\mathbb R\)

Sự biến thiên:

\(\eqalign{ & y' = 3{x^2} + 6x \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = - 2 \hfill \cr} \right. \cr}\)

- Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right) và \left( {0; + \infty } \right)\)

- Hàm số nghịch biến trên khoảng (-2;0)

- Cực trị:

Hàm số đạt cực đại tại x=-2 ; \(y_{CĐ}=0\)

Hàm số đạt cực tiểu tại x=0; \(y_{CT}=-4\)

- Giới hạn:

\(\eqalign{ & \mathop {\lim }\limits_{x \to + \infty } \left( {{x^3} + 3{x^2} - 4} \right) = + \infty \cr & \mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} + 3{x^2} - 4} \right) = - \infty \cr}\)

\(\eqalign{ & y'' = 6x + 6 \cr & y'' = 0 \Leftrightarrow x = - 1 \cr}\)

Điểm uốn I(-1;-2)

- Bảng biến thiên:

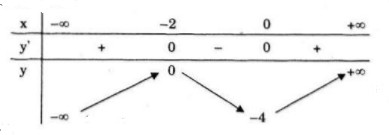
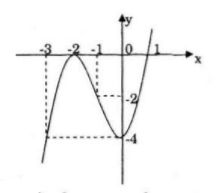
Đồ thị:

Đồ thị hàm số nhận điểm I(-1;-2) làm tâm đối xứng.

b) \(y'(-1)=-3\)

Phương trình tiếp tuyến với đồ thị tại I(-1;-2) là: \(y=-3(x+1)+(-2) \Leftrightarrow y = - 3x - 5\)

c) Đồ thị nhận I(-1;-2) làm tâm đối xứng khi và chỉ khi:

\(\eqalign{ & y\left( { - 1 + x} \right) + y\left( { - 1 - x} \right) = 2.\left( { - 2} \right) \cr & \Leftrightarrow {\left( { - 1 + x} \right)^3} + 3{\left( { - 1 + x} \right)^2} - 4 + {\left( { - 1 - x} \right)^3} + 3{\left( { - 1 - x} \right)^2} - 4 = - 4 \cr & \Leftrightarrow - 1 + 3x - 3{x^2} + {x^3} + 3 - 6x + 3{x^2} - 4 - 1 - 3x - 3{x^2} - {x^3} + 3 + 6x + 3{x^2} - 4 = - 4 \cr & \Leftrightarrow - 4 = - 4\,\,\forall x \cr}\)

\(\Leftrightarrow I(-1;-2)\) là tâm đối xứng của đồ thị.

Bài 41 trang 44 sgk Toán 12 Nâng cao Đại số và Giải tích

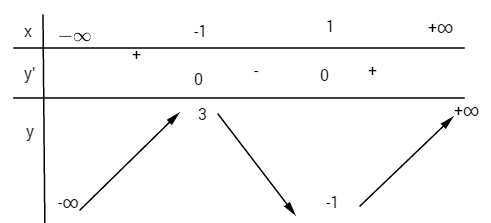
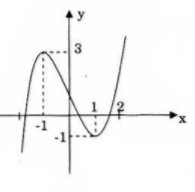
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = - {x^3} + 3{x^2} - 1\)

b) Tùy theo các giá trị của m, hãy biện luận số nghiệm của phương trình:\(- {x^3} + 3{x^2} - 1 = m\)

Giải

a) TXĐ: \(D =\mathbb R\)

\((\eqalign{ & \mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = + \infty \cr & y' = - 3{x^2} + 6x = - 3x\left( {x - 2} \right);\,\,y' = 0 \Leftrightarrow \left[ \matrix{ x = 0;\,y\left( 0 \right) = - 1 \hfill \cr x = 2;\,y\left( 2 \right) = 3 \hfill \cr} \right. \cr}\)

Bảng biến thiên:

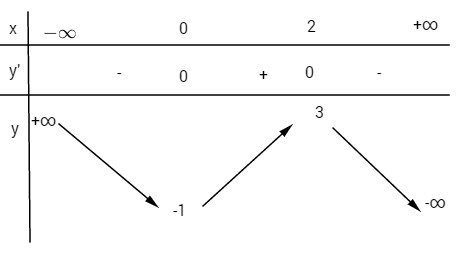
Hàm đồng biến trên khoảng (0;2), nghịch biến trên mỗi khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\)

Hàm số đạt cực tiểu tại điểm x = 0, giá trị cực tiểu\(y(0) = -1\). Hàm số đạt cực đại tại điểm x = 2, giá trị cực đại \(y(2) = 3\)

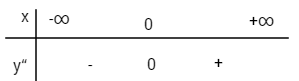
Đồ thị: \(y'' = - 6x + 6;\,\,y'' = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = 1\)

Xét dấu y”:

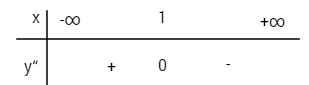
I(1;1) là điểm uốn của đồ thị

Điểm đặc biệt:

\(x = 0 \Rightarrow y = - 1\)

\(x = - 1 \Rightarrow y = 3\)

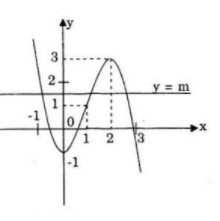
b) Số nghiệm của phương trình chính là số giao điểm của đồ thị (C) hàm số\(y = - {x^3} + 3{x^2} - 1\) với đường thẳng y = m cùng phương với trục Ox.

Dựa vào đồ thị ta có kết quả sau:

- Nếu m < -1 hoặc m > 3 thì phương trình có 1 nghiệm.

- Nếu m = -1 hoặc m = 3 thì phương trình có 2 nghiệm.

- Nếu -1 < m < 3 thì phương trình có 3 nghiệm.

Bài 42 trang 44 sgk Toán 12 Nâng cao Đại số và Giải tích

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a)\(y = {1 \over 3}{x^3} - {x^2} - 3x - {5 \over 3}\)

b) \(y = {x^3} - 3x + 1\)

c) \(y = - {1 \over 3}{x^3} + {x^2} - 2x - {2 \over 3}\)

d)\(y = {x^3} - 3{x^2} + 3x + 1\)

Giải

a) TXĐ: \(D =\mathbb R\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr & y' = {x^2} - 2x - 3;\,\,y' = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \hfill \cr x = 3 \hfill \cr} \right.;\,\,y\left( { - 1} \right) = 0;\,\,y\left( 3 \right) = {{ - 32} \over 3} \cr}\)

Bảng biến thiên:

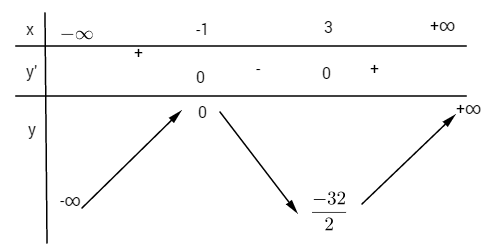
\(y'' = 2x - 2;\,y'' = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = - {{16} \over 3}\)

Xét dấu y”

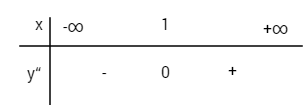
Điểm uốn\(I\left( {1; - {{16} \over 3}} \right)\)

Điểm đặc biệt:\(x = 0 \Rightarrow y = {{ - 5} \over 3}\)

Đồ thị: Đồ thị nhận \(I\left( {1; - {{16} \over 3}} \right)\)làm tâm đối xứng.

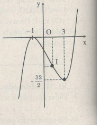
b) TXĐ:\(D =\mathbb R\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr & y' = 3{x^2} - 3;\,y' = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \hfill \cr x = 1 \hfill \cr} \right.;\,\,y\left( { - 1} \right) = 3;\,y\left( 1 \right) = - 1 \cr}\)

Bảng biến thiên:

\(y'' = 6x;\,y'' = 0 \Leftrightarrow x = 0;\,y\left( 0 \right) = 1\)

Xét dấu y”

Điểm uốn I(0;1)

Điểm đặc biệt: \(x = 2 \Rightarrow y = 3\)

Đồ thị: Đồ thị nhận I(0;1) làm tâm đối xứng.

c) TXĐ: \(D =\mathbb R\)

\(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\,\,\mathop {\lim }\limits_{x \to - \infty } y = + \infty y' = - {x^2} + 2x - 2 < 0 với mọi x \in\mathbb R\)

Hàm số nghịch biến trên \(\mathbb R\)

Bảng biến thiên:

\(y'' = - 2x + 2;\,y'' = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = - 2\)

Xét dấu y”

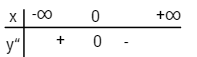
Điểm uốn I(1;-2)

Điểm đặc biết: \(x = 0 \Rightarrow y = {{ - 2} \over 3}\)

Đồ thị: Đồ thị nhận I(1;-2) làm tâm đối xứng.

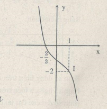
d) TXĐ: \(D =\mathbb R\)

\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty y' = 3{x^2} - 6x + 3 = 3{\left( {x - 1} \right)^2} \ge 0\)với mọi \(x \in\mathbb R\)

Dấu bằng chỉ xảy ra khi x = 1

Hàm số đồng biến trên \(\mathbb R\)

Bảng biến thiên:

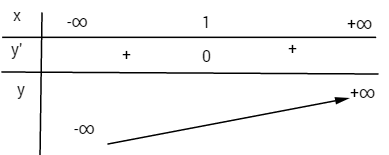
Xét dấu y”

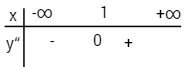
Điểm uốn I(1;2)

Điểm đặc biệt: \(x = 0 \Rightarrow y = 1\)

Đồ thị: Đồ thị nhận I(1;2) làm tâm đối xứng.

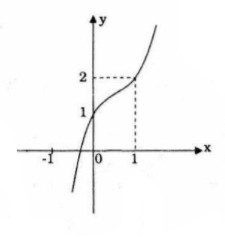
Bài 43 trang 44 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = - {x^4} + 2{x^2} - 2\)

b) Tùy theo các giá trị của m, hãy biện luận số nghiệm của phương trình \(- {x^4} + 2{x^2} - 2 = m\)

c) Viết phương trình tiếp tuyến tại các điểm uốn của đồ thị ở câu a)

Giải

a) TXĐ: \(D =\mathbb R\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to \pm \infty } y = - \infty \cr & y' = - 4{x^3} + 4x = - 4x\left( {{x^2} - 1} \right);\,y' = 0 \Leftrightarrow \left[ \matrix{ x = 0,\,\,\,\,\,\,y\left( 0 \right) = - 2 \hfill \cr x = \pm 1,\,\,\,\,y\left( { \pm 1} \right) = - 1 \hfill \cr} \right. \cr}\)

Bảng biến thiên: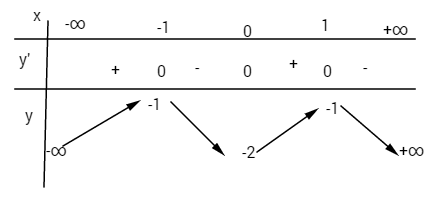

Hàm đồng biến trên các khoảng\(\left( { - \infty ; - 1} \right)\)và \(\left( {0;1} \right)\)

Hàm số nghịch biến trên các khoảng (-1;0) và \(\left( {1; + \infty } \right)\)

Hàm số đạt cực đại tại các điểm (x = -1 ; x = 1)

Giá trị cực đại \(y\left( { \pm 1} \right) = - 1\) Hàm số đạt cực tiểu tại điểm x = 0, giá trị cực tiểu y(0) = -2.

\(\eqalign{ & y'' = - 12{x^2} + 4 = - 4\left( {3{x^2} - 1} \right) \cr & y'' = 0 \Leftrightarrow x = \pm {1 \over {\sqrt 3 }};\,\,y\left( { \pm {1 \over {\sqrt 3 }}} \right) = {{ - 13} \over 9} \cr}\)

Xét dấu y”

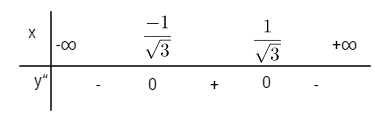
Đồ thị có hai điểm uốn \({I_1}\left( { - {1 \over {\sqrt 3 }}; - {{13} \over 9}} \right)\)và\({I_2}\left( {{1 \over {\sqrt 3 }}; - {{13} \over 9}} \right)\)

Điểm đặc biệt \(x = 2 \Rightarrow y = - 10\)

Đồ thị nhận trục tung làm trục đối xứng.

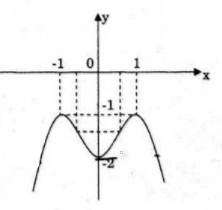
b) Số nghiệm của phương trình chính là số giao điểm của đồ thị (C) hàm số \(y = - {x^4} + 2{x^2} - 2\)với đường thẳng y = m.

Dựa vào đồ thị ta có kết quả sau:

- Nếu m < -2 thì phương trình có 2 nghiệm.

- Nếu m = -2 thì phương trình có 3 nghiệm.

- Nếu -2 < m < -1 thì phương trình có 4 nghiệm.

- Nếu m = -1 thì phương trình có 2 nghiệm.

- Nếu m> -1 thì phương trình vô nghiệm.
c) Đồ thị có hai điểm uốn\({I_1}\left( { - {1 \over {\sqrt 3 }}; - {{13} \over 9}} \right)\) và \({I_2}\left( {{1 \over {\sqrt 3 }}; - {{13} \over 9}} \right)\), phương trình tiếp tuyến của đồ thị \({I_1}\)là:

\(\eqalign{ & y + {{13} \over 9} = y'\left( { - {1 \over {\sqrt 3 }}} \right)\left( {x + {1 \over {\sqrt 3 }}} \right) \Leftrightarrow y + {{13} \over 9} = {{ - 8} \over {3\sqrt 3 }}\left( {x + {1 \over {\sqrt 3 }}} \right) \cr & \Leftrightarrow y = {{ - 8} \over {3\sqrt 3 }}x - {7 \over 3} \cr}\)

Tương tự tiếp tuyến của đồ thị \({I_2}\) là : \(y = {8 \over {3\sqrt 3 }}x - {7 \over 3}\)

Bài 44 trang 44 sgk Toán 12 Nâng cao Đại số và Giải tích

Khảo sát sự biến thiên và vẽ đồ thị hàm số sau:

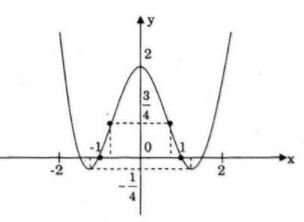
a)\(y = {x^4} - 3{x^2} + 2\)

b)\(y = - {x^4} - 2{x^2} + 1\)

Giải

a) TXĐ: \(D =\mathbb R\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \cr & y' = 4{x^3} - 6x;\,\,y' = 0 \Leftrightarrow \left[ \matrix{ x = 0;\,\,\,\,\,y\left( 0 \right) = 2 \hfill \cr x = \pm \sqrt {{3 \over 2}} ;\,\,y\left( { \pm \sqrt {{3 \over 2}} } \right) = - {1 \over 4} \hfill \cr} \right. \cr}\)

Bảng biến thiên:

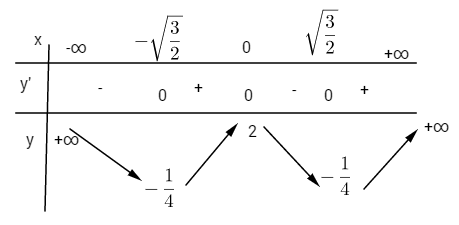
\(y'' = 12{x^3} - 6;\,\,y'' = 0 \Leftrightarrow x = \pm \sqrt {{1 \over 2}} ;\,y = \left( { \pm \sqrt {{1 \over 2}} } \right) = {3 \over 4}\)
Xét dấu y”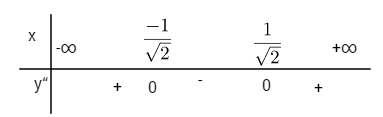

Đồ thị có hai điểm uốn \({I_1}\left( { - \sqrt {{1 \over 2}} ;{3 \over 4}} \right)\) và \({I_2}\left( {\sqrt {{1 \over 2}} ;{3 \over 4}} \right)\)

Điểm đặc biệt: \(x = \pm 1 \Leftrightarrow y = 0,x = \pm \sqrt 2 \Leftrightarrow y = 0.\)

Đồ thị: Đồ thị nhận trục tung làm trục đối xứng.

b) TXĐ:\(D =\mathbb R\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to \pm \infty } y = - \infty \cr & y' = - 4{x^3} - 4x = - 4x\left( {{x^2} + 1} \right) \cr & y' = 0 \Leftrightarrow x = 0;y\left( 0 \right) = 1 \cr}\)

Bảng biến thiên: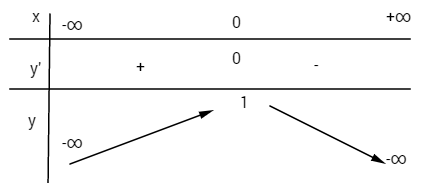

\(y'' = - 12{x^2} - 4 = - 4\left( {3{x^2} + 1} \right) < 0\) với mọi x
Đồ thị không có điểm uốn.

Điểm đặc biệt\(x = \pm 1 \Rightarrow y = - 2\)

Đồ thị:

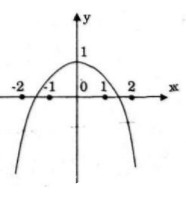
Đồ thị nhận trục tung làm trục đối xứng.

Bài 45 trang 44 sgk Toán 12 Nâng cao Đại số và Giải tích

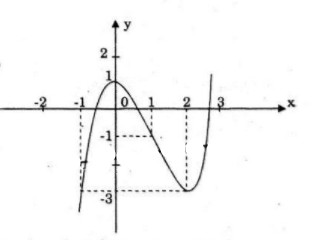
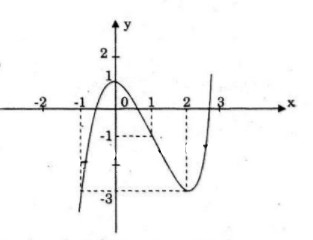
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số:\(y = {x^3} - 3{x^2} + 1\)

b) Tùy theo các giá trị của m, hãy biện luận số nghiệm của phương trình:\({x^3} - 3{x^2} + m + 2 = 0\)

Giải

a) TXĐ:\(D =\mathbb R\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr & y' = 3{x^2} - 6x = 3x\left( {x - 2} \right);\,\,y' = 0 \Leftrightarrow \left[ \matrix{ x = 0;\,\,\,\,y\left( 0 \right) = 1 \hfill \cr x = 2;\,\,\,\,y\left( 2 \right) = - 3 \hfill \cr} \right. \cr}\)

Bảng biến thiên:

Hàm số đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\); nghịch biến trên khoảng (0;2).

Hàm số đạt cực đại tại điểm x = 0, giá trị cực đại y(0) = 1; hàm số đat cực tiểu tại điểm x = 2, giá trị cực tiểu y(2) = -3

\(y'' = 6x - 6;\,y'' = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = - 1\)

Xét dấu y”

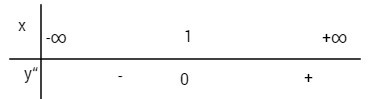
Điểm uốn của đồ thị I(1;-1)

Điểm đặc biệt\(x = - 1 \Rightarrow y = - 3\)

Đồ thị: đồ thị nhận điểm I(1;-1) làm tâm đối xứng.

b) Ta có: \({x^3} - 3{x^2} + m + 2 = 0 \Leftrightarrow {x^3} - 3{x^2} + 1 = - m - 1\)

Số nghiệm của phương trình trên bằng số giao điểm của đồ thị hàm số \(y = {x^3} - 3{x^2} + 1\) và đường thẳng y = - m -1. Dựa vào đồ thị ta có:

- Nếu \(- m - 1<-3\Rightarrow m>2\) thì phương trình có \(1\) nghiệm.

- Nếu \(-m-1=-3\Rightarrow m=2\) thì phương trình có \(2\) nghiệm.

- Nếu -3< -m-1<1=> -2<m<2 thì phương trình có 3 nghiệm.

- Nếu -m-1=1=>m=-2 thì phương trình có 2 nghiệm

- Nếu -m-1>1=>m<-2 thì phương trình có 1 nghiệm.

Bài 46 trang 44 sgk Toán 12 Nâng cao Đại số và Giải tích

Cho hàm số: \(y = \left( {x + 1} \right)\left( {{x^2} + 2mx + m + 2} \right)\)

a) Tìm các giá trị của m để đồ thị của hàm số đã cho cắt trục hoành tại 3 điểm phân biệt.

b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = -1

Giải

a) Hoành độ giao điểm của đường cong đã cho và trục hoành là nghiệm của phương trình:

\(\left( {x + 1} \right)\left( {{x^2} + 2mx + m + 2} \right) = 0 \Leftrightarrow \left[ \matrix{ x = - 1 \hfill \cr {x^2} + 2mx + m + 2 = 0\,\,\left( 1 \right) \hfill \cr} \right.\)

Đồ thị của hàm số đã cho cắt trục hoành tại 3 điểm phân biệt khi và chỉ khia phương trình (1) có hai nghiệm phân biệt khác -1, tức là:

\(\eqalign{ & \left\{ \matrix{ \Delta ' > 0 \hfill \cr f\left( { - 1} \right) \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {m^2}-m - 2 > 0 \hfill \cr - m + 3 \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ \left[ \matrix{ m < - 1 \hfill \cr m > 2 \hfill \cr} \right. \hfill \cr m \ne 3 \hfill \cr} \right. \cr & \Leftrightarrow m \in \left( { - \infty ; - 1} \right) \cup \left( {2;3} \right) \cup \left( {3; + \infty } \right). \cr}\)

b) Với m =-1 ta có \(y = \left( {x + 1} \right)\left( {{x^2} - 2x + 1} \right) = {x^3} - {x^2} - x + 1\)

TXĐ: \(D =\mathbb R\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr & y' = 3{x^2} - 2x - 1;\,y' = 0 \Leftrightarrow \left[ \matrix{ x = 1 \hfill \cr x = - {1 \over 3} \hfill \cr} \right.;\,\,y\left( 1 \right) = 0;\,\,y\left( { - {1 \over 3}} \right) = {{32} \over {27}} \cr}\)

Bảng biến thiên:

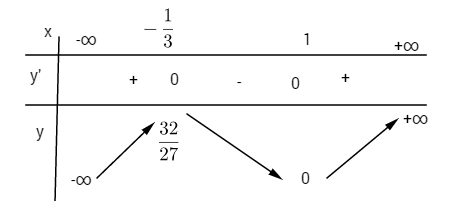
\(y'' = 6x - 2;\,y'' = 0 \Leftrightarrow x = {1 \over 3};\,y\left( {{1 \over 3}} \right) = {{16} \over {27}}\)

Xét dấu y”

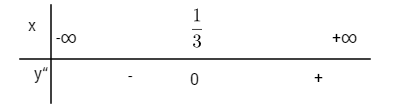
Điểm uốn \(I\left( {{1 \over 3};{{16} \over {27}}} \right)\)

Điểm đồ thị đi qua:

\(x = 0 \Rightarrow y = 1\)

\(x = 2 \Rightarrow y = 3\)

\(x = -1 \Rightarrow y = 0\)

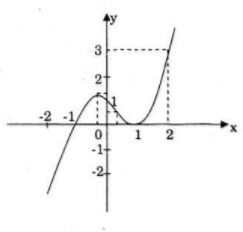
Đồ thị: Đồ thị nhận điểm uốn I làm tâm đối xứng.

Bài 47 trang 45 sgk Toán 12 Nâng cao Đại số và Giải tích

Cho hàm số: \(y = {x^4} - \left( {m + 1} \right){x^2} + m\)

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số với m = 2.

b) Chứng minh rằng đồ thị hàm số đã cho luôn đi qua hai điểm cố định với mọi giá trị của m.

Giải

a) Với m = 2 ta có: \(y = {x^4} - 3{x^2} + 2\)
TXĐ: \(D =\mathbb R\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \cr & y' = 4{x^3} - 6x;\,y' = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = \pm \sqrt {{3 \over 2}} \hfill \cr} \right.;\,\,y\left( 0 \right) = 2;\,y\left( { \pm \sqrt {{3 \over 2}} } \right) = - {1 \over 4} \cr}\)

Bảng biến thiên:

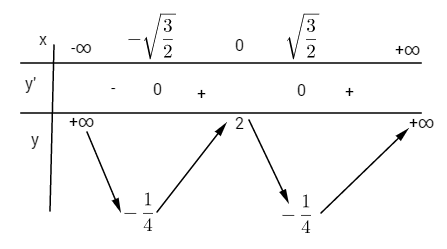
\(y'' = 12{x^2} - 6;\,y'' = 0 \Leftrightarrow x = \pm \sqrt {{1 \over 2}} ;\,y\left( { \pm \sqrt {{1 \over 2}} } \right) = {3 \over 4}\)

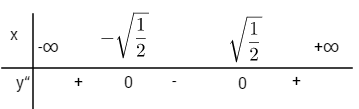
Đồ thị có hai điểm uốn :\({I_1}\left( { - \sqrt {{1 \over 2}} ;{3 \over 4}} \right)\) và \({I_2}\left( {\sqrt {{1 \over 2}} ;{3 \over 4}} \right)\)

Điểm đặc biệt

\(y = 0 \Leftrightarrow \left[ \matrix{ {x^2} = 1 \hfill \cr {x^2} = 2 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = \pm 1 \hfill \cr x = \pm \sqrt 2 \hfill \cr} \right.\)

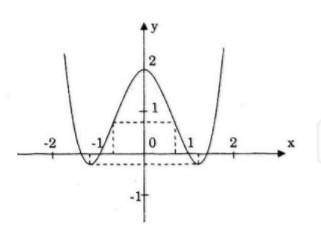
Đồ thị nhận trục tung làm trục đối xứng.

b) Đồ thị của hàm số đã cho đi qua điểm \(\left( {{x_o};{y_o}} \right)\) khi và chỉ khi

\({y_o} = x_o^4 - \left( {m + 1} \right)x_o^2 + m \Leftrightarrow \left( {1 - x_o^2} \right)m + x_o^4 - x_o^2 - {y_o} = 0\,\,\left( 1 \right)\)

Đồ thị đi qua điểm \(\left( {{x_o};{y_o}} \right)\) với moi giá trị của m khi và chỉ khi phương trình (1) nghiệm đúng với mọi m, tức là:

\(\left\{ \matrix{ 1 - x_o^2 = 0 \hfill \cr x_o^4 - x_o^2 - {y_o} = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {x_o} = 1 \hfill \cr {y_o} = 0 \hfill \cr} \right.\,\,\,\,\text{ hoặc }\,\,\,\,\left\{ \matrix{ {x_o} = - 1 \hfill \cr {y_o} = 0 \hfill \cr} \right.\)

Vậy với mọi giá trị của m, đồ thị của hàm số đã cho luôn đi qua hai điểm cố định (-1;0) và (1;0).

Bài 48 trang 45 sgk Toán 12 Nâng cao Đại số và Giải tích

Cho hàm số:\(y = {x^4} - 2m{x^2} + 2m\)

a) Tìm các giá trị của m sao cho hàm số có ba cực trị.
b) Kháo sát sự biến thiên và vẽ đồ thị của hàm số với \(m = {1 \over 2}\). Viết phương trình tiếp tuyến của đồ thị tại hai điểm uốn.

Giải

a) TXĐ:\(D =\mathbb R\)

\(y = 4{x^3} - 4mx = 4x\left( {{x^2} - m} \right);\,y' = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr {x^2} = m \hfill \cr} \right.\)

Nếu m> 0 thì \(y’=0\ \Leftrightarrow x = 0\)hoặc \(x = - \sqrt m\)hoặc \(x = \sqrt m\)

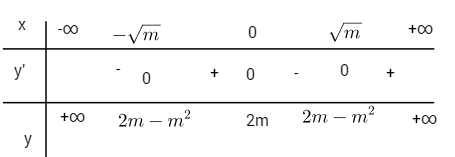
Hàm số có ba điểm cực trị.

Nếu \(m \le 0 thì {x^2} - m \ge 0\)với mọi \(x \in\mathbb R\)

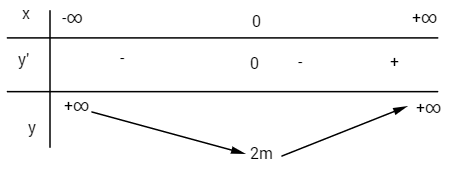
Hàm số có 1 cực tiểu.

Vậy hàm số có ba cực trị khi và chỉ khi m>0.

b) Với \(m = {1 \over 2} ta có y = {x^4} - {x^2} + 1\)

TXĐ: \(D =\mathbb R\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \cr & y' = 4{x^3} - 2x = 2x\left( {2{x^2} - 1} \right);\,y' = 0 \Leftrightarrow \left[ \matrix{ x = 0;\,\,\,\,y\left( 0 \right) = 1 \hfill \cr x = \pm \sqrt {{1 \over 2}} ;\,\,y\left( { \pm \sqrt {{1 \over 2}} } \right) = {3 \over 4} \hfill \cr} \right. \cr}\)

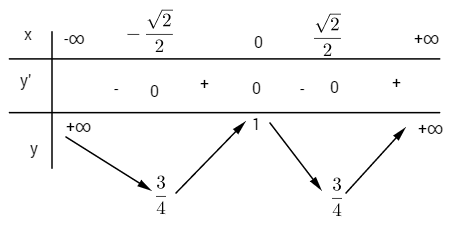
\(y'' = 12{x^2} - 2;\,y'' = 0 \Leftrightarrow x = \pm {{\sqrt 6 } \over 6};\,\,y\left( { \pm {{\sqrt 6 } \over 6}} \right) = {{31} \over {36}}\)

Xét dấu y”

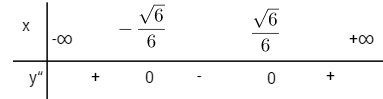
Đồ thị có hai điểm uốn: \({I_1}\left( { - {{\sqrt 6 } \over 6};{{31} \over {36}}} \right) và {I_2}\left( {{{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\)

Điểm đặc biệt: \(x = \pm 1 \Rightarrow y = 1\)

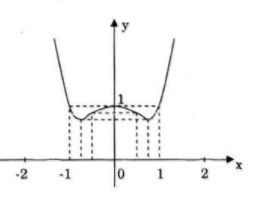
Đồ thị: Đồ thị nhận trục tung làm trục đối xứng.

+ Phương trình tiếp tuyến tại \({I_1}\left( { - {{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\)là \(y - {{31} \over {36}} = y'\left( { - {{\sqrt 6 } \over 6}} \right)\left( {x + {{\sqrt 6 } \over 6}} \right)\)

\(\Leftrightarrow y = {4 \over {3\sqrt 6 }}x + {{13} \over {12}}\)\({I_2}\left( {{{\sqrt 6 } \over 6};{{31} \over {36}}} \right) là: y = - {4 \over {3\sqrt 6 }}x + {{13} \over {12}}\)

+ Tương tự phương trình tiếp tuyến tại \({I_2}\left( {{{\sqrt 6 } \over 6};{{31} \over {36}}} \right)\)là: \(y = - {4 \over {3\sqrt 6 }}x + {{13} \over {12}}\)

Đây là tài liệu rất cần thiết để các em ôn luyện, các em có thể tự học bài ở nhà để củng cố và nắm vững kiến thức đặc biệt là chuẩn bị kiến thức để bước vào các kì thi quan trọng. Để quá trình làm bài được hiệu quả các em có thể xem thêm Giải bài tập Toán 12.

VnDoc xin giới thiệu tới các em tài liệu Giải bài tập sgk Toán 12 Nâng cao Đại số và Giải tích bài 6. Hi vọng đây sẽ là tài liệu hữu ích giúp các em đạt kết quả cao trong học tập. Cắc em có thể tham khảo thêm các tài liệu học tập khác tại mục Tài liệu học tập lớp 12 mà VnDoc đã tổng hợp và đăng tải như: Trắc nghiệm Tiếng Anh 12, Trắc nghiệm Hóa học 12,...