Giải bài tập Toán 12 Nâng cao: Câu hỏi và bài tập Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

Giải bài tập Toán 12 Nâng cao: Câu hỏi và bài tập Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số là tài liệu tham khảo hướng dẫn các em giải các bài tập sgk Toán 12 Nâng cao, giúp các em ôn luyện và nắm vững kiến thức môn Toán 12.

Bài 68 trang 61 sgk Toán 12 Nâng cao Đại số và Giải tích

Chứng minh các bất đẳng thức sau:

a) \(\tan x > x,\,\forall x \in \left( {0;{\pi \over 2}} \right)\)

b) \(\tan x > x + {{{x^3}} \over 3},\,\forall x \in \left( {0;{\pi \over 2}} \right)\)

Hướng dẫn: a) Chứng minh rằng hàm số: \(f\left( x \right) = \tan x - x\) đồng biến trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\)

Giải

a) Hàm số \(f\left( x \right) = \tan x - x\) liên tục trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\) và có đạo hàm\(f'\left( x \right) = {1 \over {{{\cos }^2}x}} - 1 > 0\,\,\forall x\left( {0;{\pi \over 2}} \right)\)

Do đó hàm số (f) đồng biến trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\)

Từ đó: \(f\left( x \right) > f\left( 0 \right)\forall x \in \left( {0;{\pi \over 2}} \right) \Leftrightarrow \tan x - x > 0\forall x \in \left( {0;{\pi \over 2}} \right)\)

b) Hàm số \(f\left( x \right) = \tan x - x - {{{x^3}} \over 3}\) liên tục trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\) và có đạo hàm \(f'\left( x \right) = {1 \over {{{\cos }^2}x}} - 1 = {\tan ^2}x - {x^2} > 0\,\,\forall x\left( {0;{\pi \over 2}} \right)\)(suy ra từ a).

Do đó hàm số (f) đồng biến trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\) và khi đó

\(f\left( x \right) = f\left( 0 \right) = 0\,\,\forall x \in \left( {0;{\pi \over 2}} \right) \Rightarrow \tan x > x + {{{x^3}} \over 3}\,\,\forall x \in \left( {0;{\pi \over 2}} \right)\)

Bài 69 trang 61 sgk Toán 12 Nâng cao Đại số và Giải tích

Xét chiều biến thiên và tìm cực trị (nếu có) của các hàm số sau:

a) \(y = \sqrt {3x + 1}\)

b) \(y = \sqrt {4x - {x^2}}\)

c) \(y = x + \sqrt x\)

d) \(y = x - \sqrt x\)

Giải

a)TXĐ: \(D = \left[ { - {1 \over 3}; + \infty } \right) y' = {3 \over {2\sqrt {3x + 1} }} > 0\,\forall x > - {1 \over 3}\)

Hàm số đồng biến \(\left( { - {1 \over 3}; + \infty } \right)\), hàm số không có cực trị.

b) TXĐ: \(D = \left[ {0;4} \right] y' = {{4 - 2x} \over {2\sqrt {4x - {x^2}} }};\,y' = 0 \Leftrightarrow x = 2;\,y\left( 2 \right) = 2\)

Bảng biến thiên

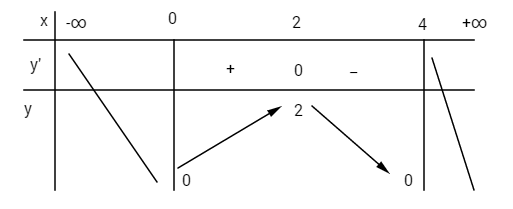
Hàm số đạt cực đại tại điểm x = 2; giá trị cực đại y(2) = 2

c) TXĐ:\(D = \left[ {0; + \infty } \right) \eqalign{ & y' = 1 + {1 \over {2\sqrt x }} = {{2\sqrt x + 1} \over {2\sqrt x }} \cr & \cr} y' = 1 + {1 \over {2\sqrt x }} > 0\,\forall x > 0\)

Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\), hàm số không có cực trị.

d) TXĐ: \(D = \left[ {0; + \infty } \right) y' = 1 - {1 \over {2\sqrt x }} y' = 0 \Leftrightarrow x = {1 \over 4}\)

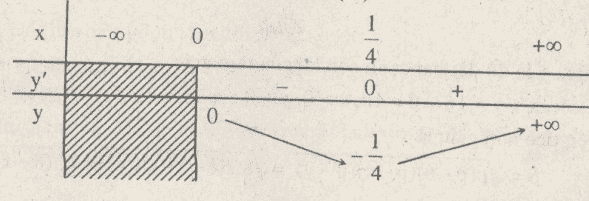
Hàm số đạt cực tiểu tại điểm \(x = {1 \over 4}\); giá trị cực tiểu\(y\left( {{1 \over 4}} \right) = - {1 \over 4}\)

Bài 70 trang 61 sgk Toán 12 Nâng cao Đại số và Giải tích

Người ta định làm một cái hộp hình trụ bằng tôn có thể tích (V) cho trước. Tìm bán kính đáy (r) và chiều cao của hình trụ sao cho tốn ít nguyên liệu nhất.

Giải

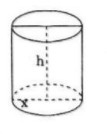
Thể tích của hình trụ là: \(V = B.h = \pi {r^2}.h \Rightarrow h = {V \over {\pi {r^2}}}\)

Diện tích toàn phần của hình trụ là:

\(S = 2\pi {r^2} + 2\pi r.h = 2\pi {r^2} + 2\pi .r.{V \over {\pi {r^2}}} = 2\pi {r^2} + {{2V} \over r}\)

Xét hàm số:

\(\eqalign{ & S\left( r \right) = 2\pi {r^2} + {{2V} \over r}\,\,\left( {r > 0} \right) \cr & S' = 4\pi r - {{2V} \over {{r^2}}} = {{4\pi {r^2} - 2V} \over {{r^2}}} \cr & S' = 0 \Leftrightarrow r = \root 3 \of {{V \over {2\pi }}} \cr}\)

Bảng biến thiên:

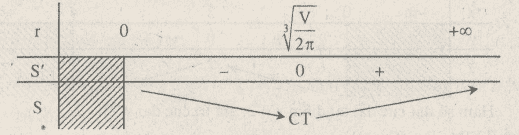
(S) đạt giá trị nhỏ nhất tại điểm \(r = \root 3 \of {{V \over {2\pi }}}\) khi đó \(h = {V \over {\pi {r^2}}} = {V \over {\pi \root 3 \of {{{{V^2}} \over {4{\pi ^2}}}} }} = \root 3 \of {{{4V} \over \pi }}\)

Bài 71 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

Chu vi của một tam giác là 16cm, độ dài một cạnh tam giác là 6cm. Tìm độ dài hai cạnh còn lại của tam giác sao cho tam giác có diện tích lớn nhất.

Hướng dẫn: Có thể áp dụng công thức Hê-rông để tính diện tích tam giác: Nếu tam giác ABC có độ dài các cạnh là a, b, c thì diện tích của nó là: \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}\) (p là nửa chu vi của tam giác.)

Giải

Gọi x, y là độ dài hai cạnh còn lại của tam giác.

Ta có: \(x + y = 16 - 6 = 10,\,x > 0,\,y > 0\)

Diện tích tam giác là: \(S = \sqrt {p\left( {p - 6} \right)\left( {p - x} \right)\left( {p - y} \right)} = \sqrt {8.2\left( {8 - x} \right)\left( {8 - y} \right)} = 4\sqrt {\left( {8 - x} \right)\left( {8 - y} \right)}\)

Thay y= 10- x , ta được \(S = 4\sqrt {\left( {8 - x} \right)\left( {x - 2} \right)} = 4\sqrt {{-x^2} + 10x - 16} \,\,\,\left( {0 < x < 10} \right)\)

S đạt giá trị lớn nhất trên khoảng (0;10) khi và chỉ khi hàm số \(f\left( x \right) = - {x^2} + 10x - 16\) đạt giá trị lớn nhất trên khoảng (0;10).

\(f'\left( x \right) = - 2x + 10;\,f'\left( x \right) = 0 \Leftrightarrow x = 5;\,f\left( 5 \right) = 9\)

Tam giác có diện tích lớn nhất khi x = 5 (cm) và y= 5 (cm)

\(\mathop {\max }\limits_{x \in \left( {0;10} \right)} f\left( x \right) = f\left( 5 \right) = 9\)

Khi đó diện tích tam giác là: \(S = 4\sqrt 9 = 12\left( {c{m^2}} \right)\)

Bài 72 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

Cho hàm số: \(f\left( x \right) = {1 \over 3}{x^3} - 2{x^2} + {{17} \over 3}\)

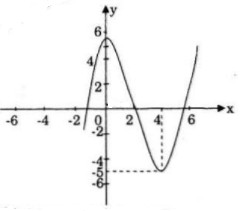
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.

b) Chứng minh rằng phương trình f(x) =0 có ba nghiệm phân biệt.

Giải

a) TXĐ: \(D =\mathbb R\)

\(\eqalign{ & \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr & y'\left( x \right) = {x^2} - 4x;\,\,\,f'\left( x \right) = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = 4 \hfill \cr} \right.;\,f\left( 0 \right) = {{17} \over 3};\,f\left( 4 \right) = - 5 \cr}\)

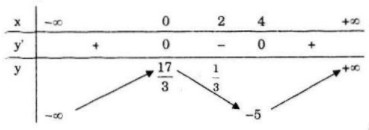
\(\eqalign{ & f''\left( x \right) = 2x - 4;\,f''\left( x \right) = 0 \Leftrightarrow x = 2 \cr & f\left( 2 \right) = {1 \over 3} \cr}\)

Điểm uốn \(I\left( {2;{1 \over 3}} \right)\)

Đồ thị nhận I làm tâm đối xứng.

b) Hàm số đã cho có cực đại và cực tiểu và giá tị cực đại, cực tiểu trái dấu, tức hai điểm cực đại và cực tiểu của đồ thị nằm về hai phía đối với trục hoành do đó đồ thị hàm số cắt trục hoành tại ba điểm phân biệt

Bài 73 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

Cho hàm số \(f\left( x \right) = {x^3} + px + q\)

a) Tìm điều kiện đối với p và q để hàm số f có một cực đại và một cực tiểu.

b) Chứng minh rằng nếu giá trị cực đại và giá trị cực tiểu trái dấu thì phương trình:\({x^3} + px + q = 0\,\,\left( 1 \right)\) có ba nghiệm phân biệt.

c) Chứng minh rằng điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là: \(4{p^3} + 27{q^2} < 0\)

Giải

a) Ta có\(f'\left( x \right) = 3{x^2} + p f'\left( x \right) = 0 \Leftrightarrow 3{x^2} + p = 0\,\,\left( 1 \right)\)

Hàm số f có một cực đại và một cực tiểu khi và chỉ khi khi phương trình (1) có hai nghiệm phân biệ t\(\Leftrightarrow p < 0\)

Khi đó hai nghiệm của (1) là: \(x = - \sqrt { - {p \over 3}} ;\,\,\,x = \sqrt { - {p \over 3}}\)

Bảng biến thiên:

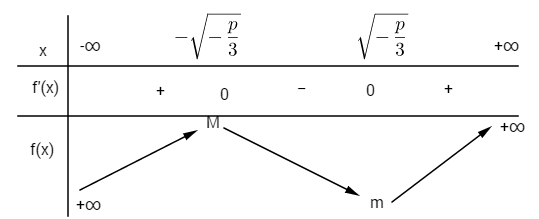
Với \(M = {\left( { - \sqrt { - {p \over 3}} } \right)^3} - p\sqrt { - {p \over 3}} +q= q - {2 \over 3}p\sqrt { - {p \over 3}}\)

\(m = {\left( {\sqrt { - {p \over 3}} } \right)^3} + p\sqrt { - {p \over 3}} + q = q + {2 \over 3}p\sqrt { - {p \over 3}}\)

b) Nếu Mm<0 và m < 0, khi đó, phương trình f(x) = 0 có ba nghiệm \(\alpha ,\,\beta ,\,\gamma với \alpha < - \sqrt { - {p \over 3}} ; - \,\sqrt { - {p \over 3}} < \beta < \sqrt { - {p \over 3}} \,\,\text{và}\,\,\gamma > \sqrt { - {p \over 3}}\)

c) Nếu Mm > 0 thì hai số M và m cùng dấu.

Nếu M < 0 và m < 0 thì phương trình (1) có nghiệm duy nhất (Lớn hơn \(\sqrt { - {p \over 3}}\))

Nếu M > 0 và m > 0 thì phương trình (1) có nghiệm duy nhất ( Nhỏ hơn \(\sqrt { - {p \over 3}}\))

Vậy điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là:

\(\left\{ \matrix{ p < 0 \hfill \cr Mm = {q^2} - {4 \over 9}{p^2}\left( { - {p \over 3}} \right) < 0 \hfill \cr} \right. \Leftrightarrow 4{p^3} + 27{q^2} < 0\)

Bài 74 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

Cho hàm số: \(f\left( x \right) = {x^3} - 3x + 1\)

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.

b) Viết phương trình tiếp tuyến của đồ thị tại điểm uốn U của nó.

c) Gọi\(\left( {{d_m}} \right)\) là đường thẳng đi qua điểm U và có hệ số góc m. Tìm các giá trị của m sao cho đường thẳng \(\left( {{d_m}} \right)\) cắt đồ thị của hàm số đã cho tại ba điểm phân biệt.

Giải

a) Tập xác định D= R

\(f'\left( x \right) = 3{x^2} - 3f'(x) = 0 \Leftrightarrow \left[ \matrix{ x = 1 \hfill \cr x = - 1 \hfill \cr} \right.\)

Hàm số đồng biến trên khoảng: \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\)

Hàm số nghịch biến trên khoảng (-1;1)

+) Cực trị:

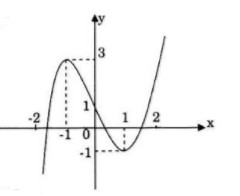
Hàm số đạt cực đại tại (x=-1; y(-1)=3)

Hàm số đạt cực tiểu tại (x=1; y(1)=-1)

+) Giới hạn:

\(\eqalign{ & \mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \cr & \mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty \cr}\)

Bảng biến thiên:

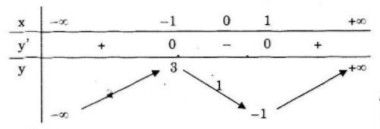
Đồ thị

Đồ thị giao trục (Oy) tại điểm (0;1)

Hàm số đồ thị nhận I(0;1) làm tâm đối xứng

b) \(f'\left( x \right) = 3{x^2} - 3\)

\(f''\left( x \right)6x;\,f''\left( x \right) = 0 \Leftrightarrow x = 0f\left( 0 \right) = 0\). Điểm uốn I(0;1)

Phương tiếp tuyến của (C) tại I là:

\(y - 1 = f'\left( 0 \right)\left( {x - 0} \right) \Leftrightarrow y = - 3x + 1\)

c) Phương trình đường thẳng\(\left( {{d_m}} \right)\) là y = mx +1.

Hoành độ giao điểm của đường thẳng \(\left( {{d_m}} \right)\) và đường cong (C) là nghiệm của phương trình

\({x^3} - 3x + 1 = mx + 1 \Leftrightarrow {x^3} - \left( {m + 3} \right)x = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr {x^2} = m + 3 \hfill \cr} \right.\)

\(\left( {{d_m}} \right)\) cắt (C) tại 3 điểm phân biệt khi và chỉ khi (1) có 3 nghiệm phân biệt, tức \(m + 3 > 0 \Leftrightarrow m > - 3\)

Bài 75 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

Cho hàm số: \(y = {x^4} - \left( {m + 1} \right){x^2} + m\)

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 2.

b) Tìm các giá trị của m sao cho đồ thị của hàm số cắt trục hoành tại bốn điểm, tạo thành ba đoạn thẳng có độ dài bằng nhau.

Giải

a) Với m=2 hàm số đã cho có dạng: \(y={x^4} - 3{x^2} + 3\)

Tập xác định: D=R

\(\eqalign{ & y' = 4{x^3} - 6x \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = {{\sqrt 6 } \over 2} \hfill \cr x = - {{\sqrt 6 } \over 2} \hfill \cr} \right. \cr}\)

Hàm số đồng biến trên khoảng: \(\left( { - {{\sqrt 6 } \over 2};0} \right)\) và \(\left( {{{\sqrt 6 } \over 2}; + \infty } \right)\)

Hàm số nghịch biến trên khoảng:\(\left( { - \infty ; - {{\sqrt 6 } \over 2}} \right)\) và \(\left( {0;{{\sqrt 6 } \over 2}} \right)\)

Cực trị:

Hàm số đạt cực đại tại (x=0; y(0)=2)

Hàm số đạt cực tiểu tại \(x = {{\sqrt 6 } \over 2}\) và \(x = - {{\sqrt 6 } \over 2}, y\left( { \pm {{\sqrt 6 } \over 2}} \right) = - {1 \over 4}\)

Giới hạn: \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty\)

Bảng biến thiên:

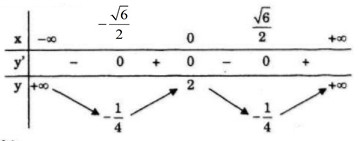
Đồ thị:

Đồ thi cắt tung độ tại điểm (0;2)

Đồ thị cắt hoành độ tại 4 điểm: \(\left( { - \sqrt 2 ;0} \right),\left( { - 1;0} \right)\left( {1;0} \right),\left( {\sqrt 2 ;0} \right)\)

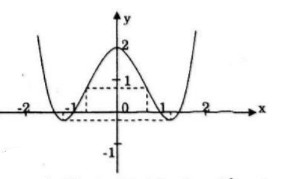
Đồ thị hàm số là hàm chẵn nhận trục Oy làm trục đối xứng.

b) Hoành độ giao điểm của đường cong (C) và trục là nghiệm phương trình

\({x^4} - \left( {m + 1} \right){x^2} + m = 0\,\,\,\left( 1 \right)\,\,\, \Leftrightarrow \left[ \matrix{ {x^2} = 1 \hfill \cr {x^2} = m \hfill \cr} \right.\)

(1) có 4 nghiệm phân biệt khi và chỉ khi m>0 và \(m \ne 1\)

Khi đó (1) có 4 nghiệm: \(x = - 1;\,x = 1;\,x = - \sqrt m ;\,x = \sqrt m - \sqrt m < - 1 < 1 < \sqrt m\)

(C) cắt trục tại 4 điểm tạo thành ba đoạn thẳng bằng nhau khi \(\sqrt m - 1 = 1 - \left( { - 1} \right) = 2 \Leftrightarrow m = 9\)

\(- 1 < - \sqrt m < \sqrt m < 1\)

(C) cắt trục hoành tại 4 điểm tạo thành ba đoạn thẳng bằng nhau khi \(1 - \sqrt m = \sqrt m - \left( { - \sqrt m } \right) = 2\sqrt m\)

Vậy m= 9 hoặc\(m = {1 \over 9}\)

Bài 76 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

Cho hàm số \(f\left( x \right) = {x^4} - {x^2}\)

a) Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho.

b) Từ đồ thị của hàm số y = f(x) suy ra cách vẽ đồ thị của hàm số\(y = \left| {f\left( x \right)} \right|\)

Giải

a) Tập xác định: D= R

\(\eqalign{ & y' = 4{x^3} - 2x \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 0 \hfill \cr x = {{\sqrt 2 } \over 2} \hfill \cr x = - {{\sqrt 2 } \over 2} \hfill \cr} \right. \cr}\)

Hàm số đồng biến trên khoảng:\(\left( { - {{\sqrt 2 } \over 2};0} \right)\) và \(\left( {{{\sqrt 2 } \over 2}; + \infty } \right)\)

Hàm số nghịch biến trên khoảng:\(\left( { - \infty ; - {{\sqrt 2 } \over 2}} \right)\) và \(\left( {0;{{\sqrt 2 } \over 2}} \right)\)

+) Cực trị:

Hàm số đạt cực đại tại: (x=0; y(0)=0)

Hàm số đạt cực tiểu tại: \(x={{\sqrt 2 } \over 2}\) và \(x=-{{\sqrt 2 } \over 2}; y\left( { \pm {{\sqrt 2 } \over 2}} \right) = - {1 \over 4}\)

+) Giới hạn:

\(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty\)

Bảng biến thiên:

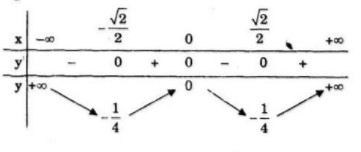
Đồ thị:

Đồ thị cắt Ox và Oy tại O(0;0); (-1;0); (1;0)

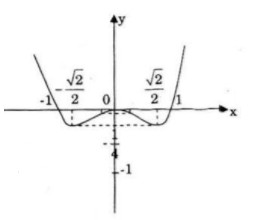
Đồ thị hàm số là hàm chẵn nên nhận trục Oy làm trục đối xứng.

b) Ta có

\(y = \left| {f\left( x \right)} \right| = \left\{ \matrix{ f\left( x \right)\,\,\,\text{nếu}\,\,\,f\left( x \right) \ge 0 \hfill \cr - f\left( x \right)\,\,\,\text{nếu}\,\,\,f\left( x \right) < 0 \hfill \cr} \right.\)

Suy ra cách vẽ đồ thị của hàm số \(y = \left| {f\left( x \right)} \right|\)

Giữ nguyên phần đồ thị hàm số y = f(x) ở phía trên trục hoành. Lấy phần đồ thị hàm số ở phía dưới trục hoành đối xứng qua trục hoành. Hợp hai phần đồ thị trên ta được đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\)

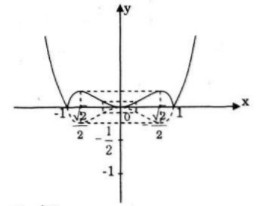
Bài 77 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

Cho hàm số: \(y = {{x - 4m} \over {2\left( {mx - 1} \right)}}.\,\,\,\left( {{H_m}} \right)\)

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m =1.
b) Chứng minh rằng với mọi\(m \ne \pm {1 \over 2}\), các đường cong \(\left( {{H_m}} \right)\) đều đi qua hai điểm cố định A và B.

Giải

a) m=1 hàm số có dạng: \(y = {{x - 4} \over {2x - 2}}\)

Tập xác định: \(D = R\backslash \left\{ 1 \right\} y' = {6 \over {{{\left( {2x - 2} \right)}^2}}} > 0\,,\forall x \in D\)

Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right) và \left( {1; + \infty } \right)\)

Hàm số không có cực trị

Giới hạn:

\(\mathop {\lim y}\limits_{x \to {1^ - }} = + \infty ;\mathop {\lim y}\limits_{x \to {1^ + }} = - \infty\)

Đường tiệm cận đứng: x=1

\(\mathop {\lim }\limits_{x \to \pm \infty } y = {1 \over 2}\)

Đường tiệm cận ngang \(y={1 \over 2}\)

Bảng biến thiên:

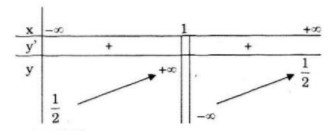
Đồ thị:

Đồ thị giao Ox, Oy tại các điểm: (4;0); (0;2)

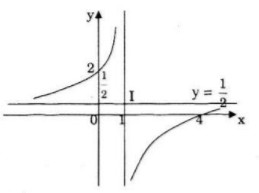
b) Gọi\(M\left( {{x_o};{y_o}} \right)\)là một điểm bất kì của mặt phẳng tọa độ. Đường cong\(\left( {{H_m}} \right)\)đi qua điểm M khi và chỉ khi m là nghiệm của phương trình \({{{x_o} - 4m} \over {2\left( {m{x_o} - 1} \right)}} = {y_o}\)

\(\Leftrightarrow \left\{ \matrix{ m{x_o} - 1 \ne 0 \hfill \cr 2{y_o}\left( {m{x_o} - 1} \right) = {x_o} - 4m \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ m{x_o} \ne 1\,\,\,\,\,\,\left( 1 \right) \hfill \cr \left( {2{x_o}{y_o} + 4} \right)m - {x_o} - 2{y_o} = 0\,\,\,\left( 2 \right) \hfill \cr} \right.\)

Mọi đường cong \(\left( {{H_m}} \right)\) với\(m \ne \pm {1 \over 2}\)đều đi qua điểm \(M\left( {{x_o};{y_o}} \right)\) khi và chỉ khi hệ phương trình trên nghiệm đúng với mọi\(m \ne \pm {1 \over 2}\).

Phương trình (2) nghiệm đúng với mọi m khi và chỉ khi

\(\left\{ \matrix{ 2{x_o}{y_o} + 4 = 0 \hfill \cr {x_o} + 2{y_o} = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {x_o} = - 2 \hfill \cr {y_o} = 1 \hfill \cr} \right.\,\,hoac\,\,\left\{ \matrix{ {x_o} = 2 \hfill \cr {y_o} = - 1 \hfill \cr} \right.\)

Vậy\(\left( {{x_o};{y_o}} \right) =(-2;1)\) và \(\left( {{x_o};{y_o}} \right)=(2;-1)\)

Ta kiểm tra điều kiện (1)
• Với \({x_o} = - 2\), ta có \(m \ne - {1 \over 2}\)

•Với \({x_o} = 2\), ta có \(m \ne {1 \over 2}\)

Vậy mọi đường cong \(\left( {{H_m}} \right)\)với \(m \ne \pm {1 \over 2}\) đều đi qua hai điểm cố định A(-2; 1) và B(2; - 1).
c) Ta có \(y' = {{4{m^2} - 1} \over {2{{\left( {mx - 1} \right)}^2}}}\)

Hệ số góc tiếp tuyến với\(\left( {{H_m}} \right)\) tại A(-2; 1) và (B(2; - 1) là y’(-2); y'(2).

Ta có tích hai hệ số góc tiếp tuyến tại A và B là:

\(y'\left( { - 2} \right).y'\left( 2 \right) = {{4{m^2} - 1} \over {2{{\left( {-2m - 1} \right)}^2}}}.{{4{m^2} - 1} \over {2{{\left( {2m - 1} \right)}^2}}} = {1 \over 4}\) là hằng số.

Bài 78 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

a) Vẽ đồ thị (P) của hàm số \(y = {x^2} - x + 1\) và đồ thị (H) của hàm số \(y = {1 \over {x + 1}}\).

b) Tìm giao điểm của hai đường cong (P) và (H). Chứng minh rằng hia đường cong đó có tiếp tuyến chung tại giao điểm của chúng.

c) Xác định các khoảng trên đó (P) nằm phía trên hoặc phía dưới (H).

Giải

a) Đồ thị

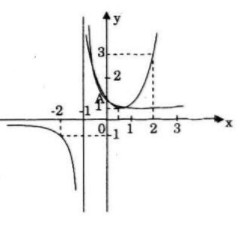
b) Hoành độ giao điể của parabol (P) và hypebol (H) là nghiệm của phương trình:

\({x^2} - x + 1 = {1 \over {x + 1}} \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - x + 1} \right) = 1\)(vì x = -1 không là nghiệm của phương trình)

\(\Leftrightarrow {x^3} + 1 = 1 \Leftrightarrow x = 0;\,\left( {y\left( 0 \right) = 1} \right)\)

Giao điểm của (P) và (H) là A(0;1)

Đặt \(f\left( x \right) = {x^2} - x + 1;\,g\left( x \right) = {1 \over {x + 1}}\)

Ta có: \(f'\left( x \right) = 2x - 1;\,g'\left( x \right) = - {1 \over {{{\left( {x + 1} \right)}^2}}} f'\left( 0 \right) = g'\left( x \right) = - 1\)

Suy ra (P) và (H) có tiếp tuyến chung tại A nên (P) và (H) tiếp xúc nhau tại điểm A.

c) Xét hiệu \(f\left( x \right) - g\left( x \right) = {x^2} - x +1 - {1 \over {x + 1}} = {{{x^3}} \over {x + 1}}\)

Bảng xét dấu f(x) – g(x)

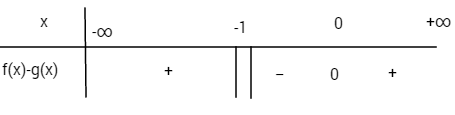
Trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0; + \infty } \right)\) (P) nằm phía trên (H). Trên khoảng \(\left( { - 1;0} \right)\)(P) nằm phía dưới (H).

Bài 79 trang 62 sgk Toán 12 Nâng cao Đại số và Giải tích

Cho hàm số : \(y = f\left( x \right) = x + {1 \over x}\)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

b) Tiếp tuyến của đường cong (C) tại điểm \(M\left( {{x_o};f\left( {{x_o}} \right)} \right)\)cắt tiệm cận đứng và tiệm cận xiên tại hai điểm A và B. Chứng minh rằng M là trung điểm của đoạn thẳng AB và tam giác OAB có diện tích không phụ thuộc vào vị trí điểm M trên đường cong (C).

Giải

a) Tập xác định: \(D = R\backslash \left\{ 0 \right\}\)\(D = R\backslash \left\{ 0 \right\}\)

\(\eqalign{ & y' = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}} \cr & y' = 0 \Leftrightarrow x = \pm 1 \cr}\)

Hàm số đồng biến trên khoảng:\(\left( { - \infty ; - 1} \right)\left( {1; + \infty } \right)\)

Hàm số nghịch biến trên khoảng: \(\left( { - 1;0} \right)\left( {0;1} \right)\)

+) Cực trị:

Hàm số đạt cực đại tại: x=-1 ; y(-1)= -2

Hàm số đạt cực tiểu tại: x=1; y(1)= 2

+) Giới hạn:

\(\mathop {\lim y}\limits_{x \to {0^ - }} = - \infty ;\mathop {\lim y}\limits_{x \to {0^ + }} = + \infty\)

Tiệm cận đứng: x= 0

\(\mathop {\lim }\limits_{x \to \pm \infty } y = \pm \infty \mathop {\lim }\limits_{x \to \infty } (y - x) = \mathop {\lim }\limits_{x \to \infty } {1 \over x} = 0\)

Tiệm cận xiên: y=x

Bảng biến thiên:

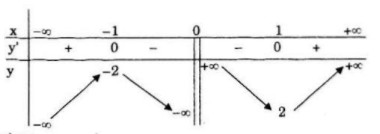
Đồ thị:

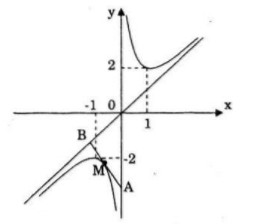
b) Tiệm cận đứng x = 0; Tiệm cận xiên y = x.
Ta có \(f\left( x \right) = 1 - {1 \over {{x^2}}}\). Phương trình tiếp tuyến của đường cong (C) tại điểm \(M\left( {{x_o};f\left( {{x_o}} \right)} \right) là y = \left( {1 - {1 \over {x_o^2}}} \right)\left( {x - {x_o}} \right) + {x_o} + {1 \over {{x_o}}}\)

Thay x = 0 vào phương trình trên, ta được tung độ của điểm A:

\({y_A} = \left( {1 - {1 \over {x_o^2}}} \right)\left( { - {x_o}} \right) + {x_o} + {1 \over {{x_o}}} = {2 \over {{x_o}}}. Vậy A\left( {0;{2 \over {{x_o}}}} \right)\)

Hoành độ của điểm B là nghiệm của phương trình

\(\left( {1 - {1 \over {x_o^2}}} \right)\left( {x - {x_o}} \right) + {x_o} + {1 \over {{x_o}}} = x \Leftrightarrow - {x \over {{x_o}}} + {2 \over {{x_o}}} = 0 \Leftrightarrow x = 2{x_o} {x_B} = 2{x_o}\). Vậy \(B\left( {2{x_o};2{x_o}} \right)\)

Ta có: \({x_M} = {x_o} = {{0 + 2{x_o}} \over 2} = {{{x_A} + {x_B}} \over 2}\)

Vì ba điểm A, M, B thẳng hàng nên từ đó suy ra rằng M là trung điểm của đoạn thẳng AB.

Diện tích tam giác OAB là

\(S = {1 \over 2}\left| {{y_A}} \right|\left| {{y_B}} \right| = {1 \over 2}\left| {{2 \over {{x_o}}}} \right|\left| {2{x_o} } \right|=2\,\,\,\forall {x_o} \ne 0\)

Tài liệu cung cấp lời giải chi tiết các bài tập trong sách giáo khoa, bám sát những nội dung kiến thức các em đã được học. Các em có thể tự học bài ở nhà và chuẩn bị kiến thức cho mình để bước vào những kì thi quan trọng trong đó có kì thi THPT Quốc gia. Các em có thể tham khảo thêm Giải bài tập Toán 12 Nâng cao để đạt hiệu quả cao.

VnDoc xin giới thiệu tới các em Giải bài tập Toán 12 Nâng cao: Câu hỏi và bài tập Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số . Hi vọng tài liệu sẽ giúp các em có thêm những phương pháp giải bài tập thật hiệu quả để đạt hiệu quả cao trong quá trình làm bài. Các em có thể tham khảo thêm các tài liệu khác tại mục Tài liệu học tập lớp 12 do VnDoc tổng hợp và đăng tải như: Trắc nghiệm Tiếng Anh 12, Trắc nghiệm Hóa học 12, Trắc nghiệm Sinh học 12,....