VnDoc.com

Giải bài tập Toán 12 Nâng cao Đại số và Giải tích bài 1

Tính đơn điệu của hàm số

Bài trước

Bài sau

Giải bài tập Toán 12 Nâng cao Đại số và Giải tích bài 1 tích hợp và hướng dẫn giải các dạng bài tập về phần đại số của môn Toán 12 nâng cao.Tài liệu được trình bày một cách cụ thể, rõ ràng để các em nắm bắt kiến thức.

Giải bài tập sgk Toán 12 Nâng cao bài 1

Bài 1 trang 7 SGK Đại số và Giải tích 12 Nâng cao
Bài 2 trang 7 SGK Đại số và Giải tích 12 Nâng cao
Bài 3 trang 7 SGK Đại số và Giải tích 12 Nâng cao
Bài 4 trang 7 SGK Đại số và Giải tích 12 Nâng cao
Bài 5 trang 8 SGK Đại số và Giải tích 12 Nâng cao
Bài 6 trang 8 SGK Đại số và Giải tích 12 Nâng cao
Bài 7 trang 8 SGK Đại số và Giải tích 12 Nâng cao
Bài 8 trang 8 SGK Đại số và Giải tích 12 Nâng cao.
Bài 9 trang 9 SGK Đại số và Giải tích 12 Nâng cao.
Bài 10 trang 9 SGK Đại số và Giải tích 12 Nâng cao.

Bài 1 trang 7 SGK Đại số và Giải tích 12 Nâng cao

Xét chiều biến thiên của các hàm số sau:

$a) y = 2{x^3} + 3{x^2} + 1$ $a) y = 2{x^3} + 3{x^2} + 1$

$b) \,y = {x^3} - 2{x^2} + x + 1$ $b) \,y = {x^3} - 2{x^2} + x + 1$

$c) y = x + {3 \over x}$ $c) y = x + {3 \over x}$

d) $y = x - {2 \over x}$ $y = x - {2 \over x}$

e) $y = {x^4} - 2{x^2} - 5$ $y = {x^4} - 2{x^2} - 5$

$f) y = \sqrt {4 - {x^2}}$ $f) y = \sqrt {4 - {x^2}}$

Giải

a) Tập xác định: $D =\mathbb R$ $D =\mathbb R$

$\eqalign{ & y$ $\eqalign{ & y' = 6{x^2} + 6x \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 0\,\,\left( {y = 1} \right) \hfill \cr x = - 1\,\,\left( {y = 2} \right) \hfill \cr} \right. \cr}$

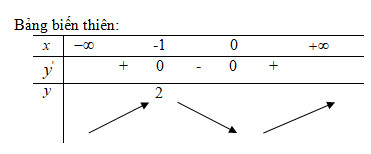
Giải bài tập toán 12 nâng cao bài 1 câu a

Hàm số đồng biến trên mỗi khoảng $\left( { - \infty ; - 1} \right)$ $\left( { - \infty ; - 1} \right)$và $\left( {0; + \infty } \right)$ $\left( {0; + \infty } \right)$nghịch biến trên khoảng $\left( { - 1;0} \right)$ $\left( { - 1;0} \right)$

b) Tập xác định: $D =\mathbb R$ $D =\mathbb R$

$\eqalign{ & y$ $\eqalign{ & y' = 3{x^2} - 4x + 1 \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = 1\,\,\left( {y = 1} \right) \hfill \cr x = {1 \over 3}\,\,\left( {y = {{31} \over {27}}} \right) \hfill \cr} \right. \cr}$

Bảng biến thiên

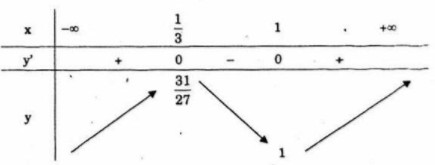
Giải bài tập Toán 12 nâng cao bài 1 câu b

Hàm số đồng biến trên mỗi khoảng $\left( { - \infty ;{1 \over 3}} \right)$ $\left( { - \infty ;{1 \over 3}} \right)$ và $\,\left( {1; + \infty } \right)$ $\,\left( {1; + \infty } \right)$, nghịch biến trên khoảng $\,\left( {{1 \over 3};1} \right)$ $\,\left( {{1 \over 3};1} \right)$.

c) Tập xác định: $D =\mathbb R\backslash \left\{ 0 \right\}$ $D =\mathbb R\backslash \left\{ 0 \right\}$

$\eqalign{ & y$ $\eqalign{ & y' = 1 - {3 \over {{x^2}}} = {{{x^2} - 3} \over {{x^2}}} \cr & y' = 0 \Leftrightarrow \left[ \matrix{ x = \sqrt 3 \,\,\left( {y = 2\sqrt 3 } \right) \hfill \cr x = - \sqrt 3 \,\,\left( {y = - 2\sqrt 3 } \right) \hfill \cr} \right. \cr}$

Bảng biến thiên

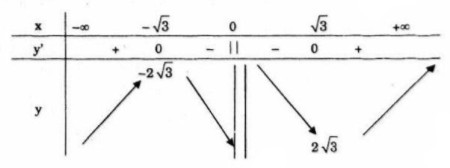
Giải bài tập toán 12 nâng cao bài 1 câu c

Hàm số đồng biến trên mỗi khoảng $\left( { - \infty ; - \sqrt 3 } \right)$ $\left( { - \infty ; - \sqrt 3 } \right)$ và $\,\left( {\sqrt 3 ; + \infty } \right)$ $\,\left( {\sqrt 3 ; + \infty } \right)$, nghịch biến trên khoảng $\left( { - \sqrt 3 ;0} \right)$ $\left( { - \sqrt 3 ;0} \right)$ và $\,\left( {0;\sqrt 3 } \right)$ $\,\left( {0;\sqrt 3 } \right)$

d) Tập xác định: $D = \mathbb R\backslash \left\{ 0 \right\}$ $D = \mathbb R\backslash \left\{ 0 \right\}$

Hàm số đồng biến trên mỗi khoảng $\,\,\left( { - \infty ;0} \right)$ $\,\,\left( { - \infty ;0} \right)$ và $\left( {0; + \infty } \right)$ $\left( {0; + \infty } \right)$

e) Tập xác định: $D= \mathbb R$ $D= \mathbb R$

$y' = 4{x^3} - 4x = 4x\left( {{x^2} - 1} \right)$;$y' = 0$

$\Leftrightarrow \,$ $\Leftrightarrow \,$ $\left[ \matrix{ x = 0\,\,\,\,\left( {y = - 5} \right) \hfill \cr x = \pm 1\,\,\,\,\left( {y = - 6} \right) \hfill \cr} \right.$ $\left[ \matrix{ x = 0\,\,\,\,\left( {y = - 5} \right) \hfill \cr x = \pm 1\,\,\,\,\left( {y = - 6} \right) \hfill \cr} \right.$

Bảng biến thiên

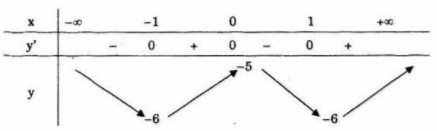
Giải bài tập toán nâng cao bài 1 câu e

Hàm số đồng biến trên mỗi khoảng $\,\left( { - \infty ; - 1} \right)$ $\,\left( { - \infty ; - 1} \right)$và $\left( {0;1} \right)$ $\left( {0;1} \right)$, đồng biến trên mỗi khoảng $\left( { - 1;0} \right)$ $\left( { - 1;0} \right)$ và $\left( {1; + \infty } \right)$ $\left( {1; + \infty } \right)$

f) Hàm số xác định khi và chỉ khi $4 - {x^2} \ge 0$ $4 - {x^2} \ge 0$ $\Leftrightarrow$ $\Leftrightarrow$ $- 2 \le x \le 2$ $- 2 \le x \le 2$

Tập xác định: $D = \left[ { - 2;2} \right]$ $D = \left[ { - 2;2} \right]$

$y' = {{ - 2x} \over {2\sqrt {4 - {x^2}} }} = {{ - x} \over {\sqrt {4 - {x^2}} }};y' = 0 \Leftrightarrow x = 0\,\,\,\left( {y = 2} \right)$

Bảng biến thiên $\left( {1; + \infty } \right)$ $\left( {1; + \infty } \right)$

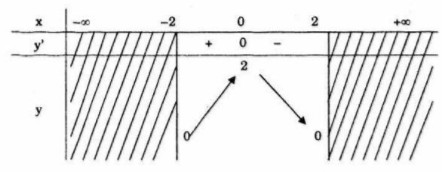
Giải bài tập Toán 12 nâng cao câu f

Hàm số đồng biến trên khoảng $\left( { - 2;0} \right)$ $\left( { - 2;0} \right)$và nghịch biến trên khoảng $\left( {0;2} \right)$ $\left( {0;2} \right)$ .

Bài 2 trang 7 SGK Đại số và Giải tích 12 Nâng cao

Chứng minh rằng:

a) Hàm số $y = {{x - 2} \over {x + 2}}$ $y = {{x - 2} \over {x + 2}}$ đồng biến trên mỗi khoảng xác định của nó.

b)Hàm số $y = {{ - {x^2} - 2x + 3} \over {x + 1}}$ $y = {{ - {x^2} - 2x + 3} \over {x + 1}}$ nghịch biến trên mỗi khoảng xác định của nó.

Giải

a) Tập xác định:

$D =\mathbb R\backslash \left\{ { - 2} \right\}y$ $D =\mathbb R\backslash \left\{ { - 2} \right\}y' = {{\left| \matrix{ 1\,\,\,\, - 2 \hfill \cr 1\,\,\,\,\,\,\,\,2 \hfill \cr} \right|} \over {{{\left( {x + 2} \right)}^2}}} = {4 \over {{{\left( {x + 2} \right)}^2}}} > 0 vớimọi x \ne - 2$

Hàm số đồng biến trên mỗi khoảng $\left( { - \infty ; - 2} \right)$ $\left( { - \infty ; - 2} \right)$ và $\left( { - 2; + \infty } \right)$ $\left( { - 2; + \infty } \right)$

b)Tập xác định:

$D =\mathbb R\backslash \left\{ { - 1} \right\}(y$ $D =\mathbb R\backslash \left\{ { - 1} \right\}(y' = {{\left( { - 2x - 2} \right)\left( {x + 1} \right) - \left( { - {x^2} - 2x + 3} \right)} \over {{{\left( {x + 1} \right)}^2}}} = {{ - {x^2} - 2x - 5} \over {{{\left( {x + 1} \right)}^2}}} < 0 với mọi x \ne - 1$

Hàm số nghịch biến trên mỗi khoảng $\left( { - \infty ; - 1} \right)$ $\left( { - \infty ; - 1} \right)$và $\left( { - 1; + \infty } \right)$ $\left( { - 1; + \infty } \right)$

Bài 3 trang 8 SGK Đại số và Giải tích 12 Nâng cao

Chứng minh rằng các hàm số sau đây đồng biến trên $\mathbb R$ $\mathbb R$

a) $f\left( x \right)$ $f\left( x \right)$= ${x^3} - 6{x^2} + 17x + 4$ ${x^3} - 6{x^2} + 17x + 4$

b) $f\left( x \right)$ $f\left( x \right)$= ${x^3} + x - \cos x - 4$ ${x^3} + x - \cos x - 4$

Giải

a) Tập xác định: $D =\mathbb R$ $D =\mathbb R$

$f'\left( x \right) = 3{x^2} - 12x + 17 > 0$ với mọi $x \in \mathbb R (vì a > 0,\Delta$ $x \in \mathbb R (vì a > 0,\Delta ' < 0)$

Hàm số đồng biến trên $\mathbb R$ $\mathbb R$

b) Tập xác định: $D =\mathbb R$ $D =\mathbb R$

$f'\left( x \right) = 3{x^2} + 1 + \sin x$

Vì $1 + \sin x \ge 0 và 3{x^2} \ge 0$ $1 + \sin x \ge 0 và 3{x^2} \ge 0$ nên $f'\left( x \right) \ge 0$ với mọi $x \in \mathbb R$ $x \in \mathbb R$, với $x = 0$ thì $1 + \sin x = 1 > 0$ $1 + \sin x = 1 > 0$nên $f'\left( x \right) > 0\,\,\,\forall x \in \mathbb R$ do đó hàm số đồng biến trên $\mathbb R$ $\mathbb R$

Bài 4 trang 8 SGK Đại số và Giải tích 12 Nâng cao

Với các giá trị nào của a hàm số $y = ax - {x^3}$ nghịch biến trên $\mathbb R$ $\mathbb R$

Giải

Tập xác định: $D=\mathbb R$ $D=\mathbb R$

$y' = a - 3{x^2}$

• Nếu $a < 0 thì y' < 0 với mọi x \in {\mathbb R}$, khi đó hàm số nghịch biến trên $\mathbb R$ $\mathbb R$

• Nếu $a = 0 thì y' = - 3{x^2} \le 0$với mọi $x \in {\mathbb R}$ $x \in {\mathbb R}$,$y'=0\Leftrightarrow x=0$.

Vậy hàm số nghịch biến trên $\mathbb R$ $\mathbb R$.

• Nếu $a > 0 thì y' = 0 \Leftrightarrow x = \pm {\sqrt {a \over 3}}$

Bảng biến thiên

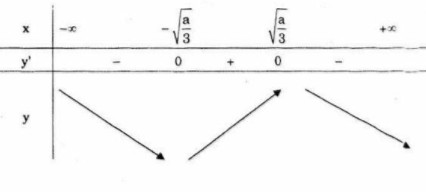
Giải bài tập toán SGK 12 nâng cao bài 4

Trong trường hợp này, hàm số không đồng biến trên ${\mathbb R}$ ${\mathbb R}$

Vậy hàm số nghịch biến trên ${\mathbb R}$ ${\mathbb R}$ khi và chỉ khi $a \le 0$ $a \le 0$

Bài 5 trang 8 SGK Đại số và Giải tích 12 Nâng cao

Tìm các giá trị của tham số$a$ để hàm số $f\left( x \right) = {1 \over 3}{x^3} + a{x^2} + 4x + 3$ $f\left( x \right) = {1 \over 3}{x^3} + a{x^2} + 4x + 3$đồng biến trên $\mathbb R$ $\mathbb R$

Giải

Tập xác định $D = \mathbb Rf$ $D = \mathbb Rf'\left( x \right) = {x^2} + 2ax + 4; \Delta = {a^2} - 4$

Hàm số đồng biến trên $\mathbb R$ $\mathbb R$ khi và chỉ khi:

$(f'\left( x \right) \ge 0,\,\forall x \in\mathbb R \Leftrightarrow \left\{ \matrix{ 1 > 0 \hfill \cr \Delta ' \le 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ 1 > 0 \hfill \cr {a^2} - 4 \le 0 \hfill \cr} \right. \Leftrightarrow - 2 \le a \le 2$

Vậy $- 2 \le a \le 2$ $- 2 \le a \le 2$ thỏa mãn yêu cầu của bài toán

Bài 6 trang 8 SGK Đại số và Giải tích 12 Nâng cao

Xét chiều biến thiên của các hàm số sau:

a) $y = {1 \over 3}{x^3} - 2{x^2} + 4x - 5$ $y = {1 \over 3}{x^3} - 2{x^2} + 4x - 5$

b) $y = - {4 \over 3}{x^3} + 6{x^2} - 9x - {2 \over 3}$ $y = - {4 \over 3}{x^3} + 6{x^2} - 9x - {2 \over 3}$

c) $y = {{{x^2} - 8x + 9} \over {x - 5}}$ $y = {{{x^2} - 8x + 9} \over {x - 5}}$

d) $y = \sqrt {2x - {x^2}}$ $y = \sqrt {2x - {x^2}}$

e) $y = \sqrt {{x^2} - 2x + 3}$ $y = \sqrt {{x^2} - 2x + 3}$

f) $y = {1 \over {x + 1}} - 2x$ $y = {1 \over {x + 1}} - 2x$

Giải

a) TXĐ: $D=\mathbb R$ $D=\mathbb R$
$y' = {x^2} - 4x + 4 = {\left( {x - 2} \right)^2} \ge 0, \forall x \in \mathbb R$ dấu bằng chỉ xảy ra khi $x=2$

Vậy hàm số đồng biến trên $\mathbb R$ $\mathbb R$

b) TXĐ: $D=\mathbb R$ $D=\mathbb R$

$y' = - 4{x^2} + 12x - 9 = - \left( {4{x^2} - 12x + 9} \right) = - {\left( {2x - 3} \right)^2} \le 0,\forall x \in \mathbb R$ dấu bằng chỉ xảy ra khi $x = {3 \over 2}$ $x = {3 \over 2}$ Vậy hàm số nghịch biến trên $\mathbb R$ $\mathbb R$

c) TXĐ: $D = \mathbb R\backslash \left\{ 5 \right\}$ $D = \mathbb R\backslash \left\{ 5 \right\}$

$y' = {{\left( {2x - 8} \right)\left( {x - 5} \right) - \left( {{x^2} - 8x + 9} \right)} \over {{{\left( {x - 5} \right)}^2}}} = {{{x^2} - 10x + 31} \over {{{\left( {x - 5} \right)}^2}}} > 0$với mọi $x \ne 5$ $x \ne 5$

Vậy hàm số đồng biến trên mỗi khoảng $\left( { - \infty ;5} \right)$ $\left( { - \infty ;5} \right)$ và $\left( {5; + \infty } \right)$ $\left( {5; + \infty } \right)$

d) Hàm số xác định khi và chỉ khi $2x - {x^2} \ge 0 \Leftrightarrow 0 \le x \le 2$ $2x - {x^2} \ge 0 \Leftrightarrow 0 \le x \le 2$

TXĐ: $D = \left[ {0;2} \right]y$ $D = \left[ {0;2} \right]y' = {{2 - 2x} \over {2\sqrt {2x - {x^2}} }} = {{1 - x} \over {\sqrt {2x - {x^2}} }};y' = 0 \Leftrightarrow x = 1\,\,\,\,\left( {y = 1} \right)$

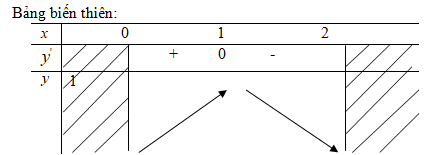
Giải bài tập Toán 12 nâng cao bài 6 câu d

Hàm số đồng biến trên khoảng $\left( {0;1} \right)$ $\left( {0;1} \right)$và nghịch biến trên khoảng $\left( {1;2} \right)$ $\left( {1;2} \right)$

e) TXĐ: $D = \mathbb R(vì {x^2} - 2x + 3 > 0,\forall x \in \mathbb R)$ $D = \mathbb R(vì {x^2} - 2x + 3 > 0,\forall x \in \mathbb R)$

$y' = {{2x - 2} \over {2\sqrt {{x^2} - 2x + 3} }} = {{x - 1} \over {\sqrt {{x^2} - 2x + 3} }}; y' = 0 \Leftrightarrow x = 1\,\,\,(y = \sqrt 2 )$

Bảng biến thiên

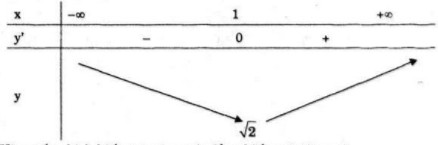
Giải bài tập Toán 12 nâng cao bài 6 câu e

Hàm số nghịch biến trên khoảng $\left( { - \infty ;1} \right)$ $\left( { - \infty ;1} \right)$ và đồng biến trên khoảng $\left( {1; + \infty } \right)$ $\left( {1; + \infty } \right)$

f) TXĐ: $D =\mathbb R \backslash \left\{ { - 1} \right\}$ $D =\mathbb R \backslash \left\{ { - 1} \right\}$

$y' = - {1 \over {{{\left( {x + 1} \right)}^2}}} - 2 < 0,\,\,\forall x \ne - 1$

Hàm số nghịch biến trên khoảng $\left( { - \infty ; - 1} \right)$ $\left( { - \infty ; - 1} \right)$ và đồng biến trên khoảng $\left( { - 1; + \infty } \right)$ $\left( { - 1; + \infty } \right)$

Bài 7 trang 8 SGK Đại số và Giải tích 12 Nâng cao

Chứng minh rằng hàm số: $f\left( x \right) = \cos 2x - 2x + 3$ $f\left( x \right) = \cos 2x - 2x + 3$ nghịch biến trên $\mathbb R$ $\mathbb R$

Giải

TXĐ: $D=\mathbb R$ $D=\mathbb R$

$f'\left( x \right) = - 2\sin 2x - 2 \le 0\Leftrightarrow - 2\left( {\sin 2x + 1} \right) \le 0,\forall x \in \mathbb R$

$f'\left( x \right) = 0 \Leftrightarrow \sin 2x = - 1 \Leftrightarrow 2x = - {\pi \over 2} + k2\pi ,k \in \mathbb Z\Leftrightarrow x = - {\pi \over 4} + k\pi ,k \in \mathbb Z$

Hàm số nghịch biến trên mỗi đoạn $\left[ { - {\pi \over 4} + k\pi ; - {\pi \over 4} + k\pi + \pi } \right]$ $\left[ { - {\pi \over 4} + k\pi ; - {\pi \over 4} + k\pi + \pi } \right]$

Do đó hàm số nghịch biến trên mỗi $\mathbb R$ $\mathbb R$

Bài 8 trang 8 SGK Đại số và Giải tích 12 Nâng cao

Chứng minh các bất đẳng thức sau:

a) $\sin x < x với mọi x > 0,\sin x > x$ $\sin x < x với mọi x > 0,\sin x > x$ với mọi $x < 0$

b) $\cos x > 1 - {{{x^2}} \over 2}$ $\cos x > 1 - {{{x^2}} \over 2}$ với mọi $x \ne 0$ $x \ne 0$

c) $\sin x > x - {{{x^3}} \over 6}$ $\sin x > x - {{{x^3}} \over 6}$ với mọi $x > 0; \sin x < x - {{{x^3}} \over 6}$ $x > 0; \sin x < x - {{{x^3}} \over 6}$với mọi $x<0$

Giải

a) Hàm số $f\left( x \right) = x - \sin x$ $f\left( x \right) = x - \sin x$ liên tục trên nửa khoảng $\left[ {0;{\pi \over 2}} \right)$ $\left[ {0;{\pi \over 2}} \right)$và có đạo hàm $f'\left( x \right) = 1 - \cos x > 0$ với mọi $x \in \left( {0;{\pi \over 2}} \right)$ $x \in \left( {0;{\pi \over 2}} \right)$. Do đó hàm số đồng biến trên $\left[ {0;{\pi \over 2}} \right), từ đó với mọi x \in \left( {0;{\pi \over 2}} \right)$ $\left[ {0;{\pi \over 2}} \right), từ đó với mọi x \in \left( {0;{\pi \over 2}} \right)$ta có:

$f\left( x \right) > f\left( 0 \right) = 0 \Rightarrow x - \sin x > 0\,\,\forall x \in \left( {0;{\pi \over 2}} \right). Với x \ge {\pi \over 2} thì x > 1 \ge \sin x$ $f\left( x \right) > f\left( 0 \right) = 0 \Rightarrow x - \sin x > 0\,\,\forall x \in \left( {0;{\pi \over 2}} \right). Với x \ge {\pi \over 2} thì x > 1 \ge \sin x$

Vậy $\sin x < x với mọi (x > 0$ $\sin x < x với mọi (x > 0$

* Với mọi $x<0$, áp dụng chứng minh trên ta có:

$\sin \left( { - x} \right) < - x \Rightarrow - \sin x < - x \Rightarrow \sin x > x$ $\sin \left( { - x} \right) < - x \Rightarrow - \sin x < - x \Rightarrow \sin x > x$

Vậy $\sin x > x với mọix<0$ $\sin x > x với mọix<0$

b) Hàm số $g\left( x \right) = \cos x + {{{x^2}} \over {2 - 1}}$ $g\left( x \right) = \cos x + {{{x^2}} \over {2 - 1}}$ liên tục trên $\left[ {0; + \infty } \right)$ $\left[ {0; + \infty } \right)$và có đạo hàm $g'\left( x \right) = x - \sin x$

Theo câu a) $g'\left( x \right) > 0 với mọi x>0$nên hàm số g đồng biến trên $\left[ {0; + \infty } \right)$ $\left[ {0; + \infty } \right)$, khi đó ta có

$g\left( x \right) > g\left( 0 \right) = 0 với mọi x>0$ $g\left( x \right) > g\left( 0 \right) = 0 với mọi x>0$

tức là $\cos x + {{{x^2}} \over 2} - 1 > 0 với mọi x>0 hay \cos x > 1 - {{{x^2}} \over 2} với mọi x>0(1)$ $\cos x + {{{x^2}} \over 2} - 1 > 0 với mọi x>0 hay \cos x > 1 - {{{x^2}} \over 2} với mọi x>0(1)$

Với mọi x⁰ nên theo (1) ta có:

$\cos \left( { - x} \right) > 1 - {{{{\left( { - x} \right)}^2}} \over 2}\, \Leftrightarrow \cos x > 1 - \,{{{x^2}} \over 2} với mọi x$ $\cos \left( { - x} \right) > 1 - {{{{\left( { - x} \right)}^2}} \over 2}\, \Leftrightarrow \cos x > 1 - \,{{{x^2}} \over 2} với mọi x$

Từ (1) và (2) suy ra: \ $(\cos x > 1 - \,{{{x^2}} \over 2} với mọi x \ne 0$ $(\cos x > 1 - \,{{{x^2}} \over 2} với mọi x \ne 0$

c) Hàm số $h\left( x \right) = \sin x - x + {{{x^3}} \over 6}$ $h\left( x \right) = \sin x - x + {{{x^3}} \over 6}$có đạo hàm $h'(x) = \cos x - 1 + {{{x^2}} \over 2} > 0$ với mọi $x \ne 0$ $x \ne 0$ (câu b)

Do đó $h$ đồng biến trên $\mathbb R$ $\mathbb R$ nên ta có:

$h\left( x \right) > h\left( 0 \right) = 0,\forall x > 0 và h\left( x \right) < h\left( 0 \right) = 0,\forall x < 0$ $h\left( x \right) > h\left( 0 \right) = 0,\forall x > 0 và h\left( x \right) < h\left( 0 \right) = 0,\forall x < 0$

Từ đó suy ra: $\sin x > x - {{{x^3}} \over 6} với mọi x>0 \sin x < x - {{{x^3}} \over 6}với mọi x<0$ $\sin x > x - {{{x^3}} \over 6} với mọi x>0 \sin x < x - {{{x^3}} \over 6}với mọi x<0$

Bài 9 trang 9 SGK Đại số và Giải tích 12 Nâng cao.

Chứng minh rằng: $\sin x + \tan x > 2x với mọi x \in \left( {0;{\pi \over 2}} \right)$ $\sin x + \tan x > 2x với mọi x \in \left( {0;{\pi \over 2}} \right)$

Giải

Chứng minh hàm số $f\left( x \right) = \sin x + \tan x - 2x$ $f\left( x \right) = \sin x + \tan x - 2x$ đồng biến trên nửa khoảng $\left[ {0;{\pi \over 2}} \right)$ $\left[ {0;{\pi \over 2}} \right)$

Hàm số $f\left( x \right) = \sin x + \tan x - 2x$ $f\left( x \right) = \sin x + \tan x - 2x$ liên tục trên nửa khoảng $\left[ {0;{\pi \over 2}} \right)$ $\left[ {0;{\pi \over 2}} \right)$ và có đạo hàm:$f'\left( x \right) = \cos x + {1 \over {{{\cos }^2}x}}\, - 2$

Vì $\in \left( {0;{\pi \over 2}} \right) nên 0 < \cos x < 1 \Rightarrow \cos x > {\cos ^2}x \Rightarrow \cos x + {1 \over {{{\cos }^2}x}}\, - 2 > {\cos ^2}x + {1 \over {{{\cos }^2}x}}\, - 2 > 0$ $\in \left( {0;{\pi \over 2}} \right) nên 0 < \cos x < 1 \Rightarrow \cos x > {\cos ^2}x \Rightarrow \cos x + {1 \over {{{\cos }^2}x}}\, - 2 > {\cos ^2}x + {1 \over {{{\cos }^2}x}}\, - 2 > 0$

( $vì {\cos ^2}x + {1 \over {{{\cos }^2}x}} > 2 với mọi ,x \in \left( {0;{\pi \over 2}} \right))) Do đó f$ $vì {\cos ^2}x + {1 \over {{{\cos }^2}x}} > 2 với mọi ,x \in \left( {0;{\pi \over 2}} \right))) Do đó f'\left( x \right) > 0 với mọi x \in \left( {0;{\pi \over 2}} \right)$

Suy ra hàm số $f$ đồng biến trên $\,\left[ {0;{\pi \over 2}} \right)$ $\,\left[ {0;{\pi \over 2}} \right)$

Khi đó ta có $f\left( x \right) > f\left( 0 \right) = 0$ $f\left( x \right) > f\left( 0 \right) = 0$ với mọi $x \in \left( {0;{\pi \over 2}} \right)$ $x \in \left( {0;{\pi \over 2}} \right)$ tức là $\sin x + \tan x > 2x$ $\sin x + \tan x > 2x$ với mọi $x \in \left( {0;{\pi \over 2}} \right)$ $x \in \left( {0;{\pi \over 2}} \right)$

Bài 10 trang 9 SGK Đại số và Giải tích 12 Nâng cao

Số dân của một thị trấn sau $t$ năm kể từ năm $1970$ được ước tính bởi công thức: $f\left( t \right) = {{26t + 10} \over {t + 5}},f\left( t \right)$ $f\left( t \right) = {{26t + 10} \over {t + 5}},f\left( t \right)$ được tính bằng nghìn người).

a) Tính số dân của thị trấn vào năm $1980$và năm$1995$

b) Xem$f$ là một hàm số xác định trên nửa khoảng $\left[ {0; + \infty } \right)\,$ $\left[ {0; + \infty } \right)\,$. Tính$f'$ và xét chiều biến thiên của hàm số$f$ trên nửa khoảng $\left[ {0; + \infty } \right)\,$ $\left[ {0; + \infty } \right)\,$

c) Đạo hàm của hàm số $f$ biểu thị tốc độ tăng dân số của thị trấn ( tính bằng nghìn người/năm).

• Tính tốc độ tăng dân số vào năm $1990$và năm $2008$của thị trấn.

• Vào năm nào thì tốc độ gia tăng dân số là $0,125$ nghìn người/năm?

Giải

a) Vào năm $1980$ thì $t = 10$, số dân của thị trấn năm$1980$ là:

$f\left( {10} \right) = {{260 + 10} \over {10 + 5}} = 18$ $f\left( {10} \right) = {{260 + 10} \over {10 + 5}} = 18$nghìn người

Vào năm$1995$thì $t=25$ , số dân của thị trấn năm $1995$ là:

$f\left( {25} \right) = {{26.25 + 10} \over {25 + 5}} = 22$ $f\left( {25} \right) = {{26.25 + 10} \over {25 + 5}} = 22$nghìn người.

b) Ta có: $f'\left( t \right) = {{120} \over {{{\left( {t + 5} \right)}^2}}} > 0 với mọi t>0$

Hàm số đồng biến trên $\left[ {0; + \infty } \right)$ $\left[ {0; + \infty } \right)$

c) Tốc độ tăng dân số vào năm $1990$ là$f'\left( {20} \right) = {{120} \over {{{25}^2}}} = 0,192$

Tốc độ tăng dân số vào năm$2008$là $f'\left( {38} \right) = {{120} \over {{{43}^2}}} \approx 0,065{{120} \over {{{\left( {t + 5} \right)}^2}}} = 0,125 \Leftrightarrow t + 5 = \sqrt {{{120} \over {0,125}}} \approx 31 \Rightarrow t \approx 26$

Vào năm $1996$ tốc độ tăng dân số của thị trấn là $0,125$

VnDoc đã giới thiệu tới các em tài liệu giải bài tập Toán 12 nâng cao. Hi vọng đây sẽ là tài liệu hỗ trợ quan trọng trong quá trình ôn luyện kiến thức của các em. Tài liệu có kèm theo hướng dẫn giải chi tiết hỗ trợ các em trong quá trình làm bài, giúp các em tự ôn luyện hàng ngày mà còn trang bị kiến thức để các em tự tin bước vào các kì thi quan trọng với kết quả cao. Các em có thể xem thêm Giải bài tập Toán 12, giải vở bài tập Toán 12.

Để đạt được kết quả cao đặc biệt trong các kì thi các em có thể tham khảo thêm các tài liệu khác do VnDoc tổng hợp và đăng tải tại mục Tài liệu học tập lớp 12 như: Giải bài tập Hóa học 12 nâng cao, Giải bài tập tiếng Anh, Giải bài tập hóa học,....

Chia sẻ, đánh giá bài viết

7

1.481

Bài trước

Bài sau