Cho hàm số y = f(x) xét sự đơn điệu của hàm g(x) = f(u(x))
Cách xét tính đơn điệu của hàm hợp, hàm ẩn Toán 12
Việc xét sự đơn điệu của hàm hợp g(x) = f(u(x)) là một trong những kỹ năng quan trọng trong Giải tích lớp 12 và các chuyên đề luyện thi THPT Quốc gia. Khi nắm vững cách xác định đồng biến – nghịch biến của hàm hợp và hàm ẩn, học sinh không chỉ giải nhanh các dạng bài tập trắc nghiệm mà còn hiểu sâu bản chất đạo hàm, điều kiện đơn điệu và quan hệ giữa các hàm thành phần.
Trong bài viết này, chúng ta sẽ phân tích đầy đủ cách xét tính đơn điệu của hàm hợp, mẹo xử lý nhanh, dấu hiệu nhận biết và những lưu ý thường gặp. Đây sẽ là tài liệu tối ưu giúp bạn học chắc – nhớ lâu – áp dụng hiệu quả trong mọi bài toán liên quan đến hàm hợp.
A. PHƯƠNG PHÁP GIẢI TOÁN
Bài toán tổng quát: Cho hàm 
\(y =
f(x)\) hoặc hàm \(y =
f'(x)\) xét sự biến thiên của hàm \(g(x) = f(u(x))\).
Cách giải:
- Tính đạo hàm \(g'(x) =
f'(u(x)).u'(x)\)
- Xét dấu \(g'(x)\) dựa vào dấu của \(f'(u(x))\) và \(u'(x)\) theo quy tắc nhân dấu. Lưu ý khi xét dấu \(f'(u(x))\) dựa vào dấu của \(f'(x)\) như sau: Nếu \(f'(x)\) không đổi dấu trên \(D\) thì \(f'(u(x))\) không đổi dấu khi \(u(x) \in D\).
B. BÀI TẬP MINH HỌA XÉT SỰ ĐỒNG BIÊN NGHỊCH BIẾN CỦA HÀM SỐ
Ví dụ 1. Cho hàm số \(f(x)\), bảng xét dấu của \(f'(x)\) như sau:
Hàm số \(f(5 - 2x)\) nghịch biến trên khoảng nào dưới đây?
A. \((2;3)\). B. \((0;2)\). C. \((3;5)\). D. \((5;
+ \infty)\).
Hướng dẫn giải
Ta có
\(y = f(5 - 2x) \rightarrow y' = -
2f'(5 - 2x)\)
Hàm số nghịch biến khi \(y' = -
2f'(5 - 2x) \leq 0 \Leftrightarrow f'(5 - 2x) \geq
0\).
Dựa vào bảng xét dấu ta thấy khi \(f'(x) \geq 0 \Leftrightarrow \left\lbrack
\begin{matrix}
x \geq 1 \\
- 3 \leq x \leq - 1
\end{matrix} \right.\)
Nên \(f'(5 - 2x) \geq 0 \Leftrightarrow
\left\lbrack \begin{matrix}
5 - 2x \geq 1 \\
- 3 \leq 5 - 2x \leq - 1
\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}
3 \leq x \leq 4 \\
x \leq 2
\end{matrix} \right.\)
Vậy hàm số đã cho nghịch biến trên các khoảng \((3;4)\) và \(( - \infty;2)\).
Chọn B
Ví dụ 2. Cho hàm số \(f(x)\), bảng xét dấu của \(f'(x)\)như sau:
Hàm số \(y = f(3 - 2x)\) đồng biến trên khoảng nào dưới đây?
A. \((3\ ;\ 4)\). B. \((2\ ;\ 3)\). C. \(( - \infty\ ;\ - 3)\). D. \((0\ ;\ 2)\).
Hướng dẫn giải
Ta có: \(y = f(3 - 2x) \Rightarrow y' =
(3 - 2x)'f'(3 - 2x)\) \(= -
2f'(3 - 2x)\).
Hàm số \(y = f(3 - 2x)\) đồng biến khi \(y' = - 2f'(3 - 2x) \geq 0
\Leftrightarrow f'(3 - 2x) \leq 0 \Leftrightarrow \left\lbrack
\begin{matrix}
3 - 2x \leq - 3 \\
- 1 \leq 3 - 2x \leq 1
\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}
x \geq 3 \\
1 \leq x \leq 2
\end{matrix} \right.\).
Hàm số \(y = f(3 - 2x)\) đồng biến trên khoảng \((3; + \infty)\) nên đồng biến trên khoảng \((3;4)\).
Đáp án A
Ví dụ 3. Cho hàm số \(y = f(x)\) có bảng biến thiên như sau:
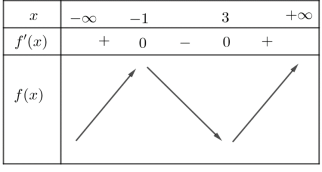
Các khoảng đồng biến của hàm số\(y = f(2x -
1)\)?
A. \(( - \infty;2)\) B. \(( - \infty;0)\) và \((2; + \infty)\) C. \(( - \infty; - 1)\) và \((0; + \infty)\) D. \((0;2)\)
Hướng dẫn giải
Ta có
\(y = f(2x - 1) \Rightarrow y' =
2f'(2x - 1)\).
Khi đó \(y' = 2f'(2x - 1) > 0
\Leftrightarrow - 1 < 2x - 1 < 3 \Leftrightarrow 0 < x <
2\).
Đáp án D.
C. BÀI TẬP VẬN DỤNG XÉT SỰ ĐƠN ĐIỆU CỦA HÀM SỐ
Bài tập 1. Cho hàm số \(y = f(x)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị hàm \(f'(x)\) như hình vẽ dưới đây:
Hàm số \(g(x) = f\left( x^{2} - x
\right)\) đồng biến trên khoảng nào?
A. \(\left( \frac{1}{2};1 \right)\). B. \((1;2)\). C. \(\left( - 1;\frac{1}{2} \right)\). D. \(( - \infty; - 1)\).
Bài tập 2. Cho hàm số \(y = f(x)\) có bảng xét dấu của đạo hàm như sau:
Số giá trị nguyên của tham số \(m\) để hàm số \(y = f\left( x^{2} + 4x + m
\right)\) nghịch biến trên \(( - 1;\ \
1)\) là
A. 2 B. 3 C. 1 D. 0
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ
------------------------------------------
Qua bài viết, bạn đã nắm được toàn bộ phương pháp xét sự đồng biến – nghịch biến của hàm hợp g(x) = f(u(x)), bao gồm điều kiện đạo hàm, mối liên hệ giữa f'(u) và u'(x), cùng những trường hợp đặc biệt thường xuất hiện trong đề thi. Khi hiểu đúng quy tắc đơn điệu của hàm số, bạn có thể xử lý trơn tru mọi bài toán hàm hợp, hàm ẩn và nâng cao khả năng tư duy giải tích.
