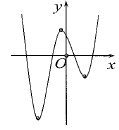Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Biện luận số điểm cực trị của hàm trị tuyệt đối

Xác định cực trị hàm trị tuyệt đối

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Lý thuyết

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Cách xác định cực trị hàm trị tuyệt đối

Trong chương trình Toán 12, phần cực trị của hàm số là nội dung quan trọng, giúp học sinh rèn luyện khả năng phân tích, tư duy logic và xử lý đạo hàm. Đặc biệt, với hàm trị tuyệt đối, việc biện luận số điểm cực trị trở nên phức tạp hơn do phải xét các khoảng giá trị khác nhau của biểu thức trong dấu trị tuyệt đối.

Bài viết này sẽ hướng dẫn chi tiết cách biện luận số điểm cực trị của hàm trị tuyệt đối, giúp học sinh hiểu rõ bản chất, nắm vững các bước giải và vận dụng linh hoạt trong các dạng bài thi trắc nghiệm và tự luận. Đồng thời, tài liệu có đáp án chi tiết và lời giải minh họa, giúp bạn học hiệu quả hơn, tránh sai sót khi xử lý bài toán cực trị.

Cách xét cực trị của hàm trị tuyệt đối

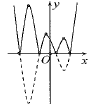
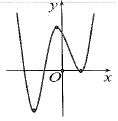
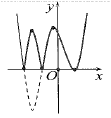
Cho hình vẽ đồ thị hàm số $y = f(x)$ có $n_{1}$ $n_{1}$ điểm cực trị. Tìm giá trị của tham số $m$ để hàm số $y = \left| f(x + k) + f(m) \right|$ $y = \left| f(x + k) + f(m) \right|$ có $n_{2}$ $n_{2}$ điểm cực trị.

Số điểm cực trị của đồ thị hàm số $y = \left| f(x + k) + f(m) \right|$ $y = \left| f(x + k) + f(m) \right|$ bằng tổng số điểm cực trị của đồ thị hàm số $y = f(x)$ và số giao điểm giữa đồ thị $y = f(x) + f(m)$ với trục $Ox$.
Khi tịnh tiến sang trái hoặc sang phải $k$ đơn vị thì số điểm cực trị hàm số $y = f(x + k)$ bằng số điểm cực trị hàm số $y = f(x)$.
Để tìm số giao điểm $y = f(x) + f(m)$ với trục $Ox$ta chuyển về dạng tìm số giao điểm của đồ thị $y = f(x)$ với đường thẳng $y = - f(m)$.

Lưu ý:

Số giao điểm này không tính giao tại điểm cực trị của hàm số $y = f(x)$. Vì nó đã được tính là cực trị của hàm $y = f(x)$.

Đồ thị hàm số $y = f(x)$

Đồ thị hàm số $y = \left| f(x) \right|$ $y = \left| f(x) \right|$

Số cực trị của hàm số $y = f(x)$ là $3$.

Số giao điểm với trục $Ox$ là $4$.

Số điểm cực trị của hàm số $y = \left| f(x) \right|$ $y = \left| f(x) \right|$ là $7$.

Mỗi giao điểm là một cực trị.

Số cực trị của hàm số $y = f(x)$ là $3$.

Số giao điểm với trục $Ox$ là $3$.

Số điểm cực trị của hàm số $y = \left| f(x) \right|$ $y = \left| f(x) \right|$ là $5$.

Khi giao với trục $Ox$ tại điểm cực trị ta sẽ không tính điểm đó là cực trị.

Một số tính chất:

Hàm số $y = f(ax + b) + c$ $(a \neq 0)$ $(a \neq 0)$ có số điểm cực trị bằng số điểm cực trị của hàm số $y = f(x)$.
Hàm số $y = \left| f(x) \right|$ $y = \left| f(x) \right|$ có số điểm cực trị bằng số điểm cực trị của hàm số $y = f(x)$ cộng số nghiệm đơn cộng số nghiệm bội lẻ của phương trình $f(x) = 0$.
Hàm số $y = f\left( |x| \right)$ $y = f\left( |x| \right)$ có số điểm cực trị bằng $2a + 1$, với $a$ là số điểm cực trị dương của hàm số $y = f(x)$.
Đặc biệt: Đối với hàm số $f(x) = ax^{3} + bx^{2} + cx + d$ $f(x) = ax^{3} + bx^{2} + cx + d$ có hai điểm cực trị $x_{1}$ $x_{1}$; $x_{2}$ $x_{2}$. Khi đó hàm số $y = \left| f(x) \right|$ $y = \left| f(x) \right|$ có $n$ điểm cực trị:

- $n = 5 \Leftrightarrow f_{cđ}.f_{ct} < 0$ $n = 5 \Leftrightarrow f_{cđ}.f_{ct} < 0$.
- $n = 3 \Leftrightarrow f_{cđ}.f_{ct} \geq 0$ $n = 3 \Leftrightarrow f_{cđ}.f_{ct} \geq 0$.

-------------------------------------------------

Qua bài viết Biện luận số điểm cực trị của hàm trị tuyệt đối, bạn đã được hệ thống hóa đầy đủ phương pháp giải và cách xác định số điểm cực trị chính xác cho từng dạng bài. Hãy luyện tập thêm với các bài tập vận dụng và nâng cao để củng cố kỹ năng, đồng thời kết hợp ôn lại các chuyên đề liên quan như hàm số, đạo hàm, cực trị, giá trị tuyệt đối nhằm đạt kết quả cao nhất trong kỳ thi THPT Quốc gia sắp tới.

Tải về

Chọn file muốn tải về: