Tìm số cực trị của hàm trị tuyệt đối – Có đáp án
Chuyên đề toán 12: Xác định cực trị của hàm trị tuyệt đối
Trong chương trình Toán 12, phần cực trị của hàm số là nội dung quan trọng giúp học sinh rèn luyện khả năng tư duy và vận dụng đạo hàm để tìm giá trị lớn – nhỏ của hàm. Đặc biệt, dạng tìm số cực trị của hàm trị tuyệt đối thường khiến nhiều bạn học sinh gặp khó khăn do phải xét nhiều trường hợp khác nhau của biểu thức bên trong dấu giá trị tuyệt đối.
Bài viết này sẽ hướng dẫn chi tiết cách tìm số cực trị của hàm trị tuyệt đối, kết hợp lý thuyết – phương pháp – bài tập có đáp án chi tiết, giúp bạn hiểu bản chất, xử lý nhanh và chính xác trong mọi tình huống, đặc biệt hữu ích khi ôn thi THPT Quốc gia môn Toán.
A. Ví dụ minh họa tìm cực trị hàm trị tuyệt đối
Ví dụ 1. Cho hàm số 
\(f(x)\) có \(f'(x) = \left( x^{2} - 4 \right)\left(x^{3} - 1 \right)^{2}\left( 3^{x} - 27 \right)(x - 25)^{3}(x -7)^{7}\). Số điểm cực đại của hàm số \(f\left( |x| \right)\) là:
A. \(10\). B. \(4\). C. \(5\). D. \(2\).
Hướng dẫn giải
Chọn B
Ta có: \(f'(x) = 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x = 2 \\
x = - 2 \\
x = 1 \\
x = 3 \\
x = 25 \\
x = 7
\end{matrix} \right.\)
Bảng biến thiên
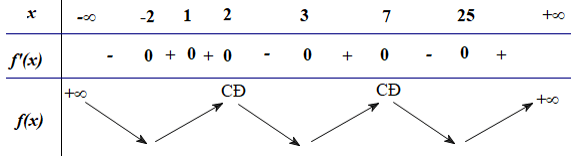
Dựa vào BBT ta có:
Hàm số \(f(x)\) có 2 điểm cực đại dương nên hàm số \(f\left( |x|
\right)\) có 4 điểm cực đại (lưu ý nếu trên khoảng \(( - 2;2)\) hàm số \(f(x)\) đồng biến thì \(f\left( |x| \right)\) đạt cực tiểu \(x = 0\)).
Ví dụ 2. Cho hàm số \(y = f(x) = ax^{4} +
bx^{3} + cx^{2} + dx + e\) có đồ thị như hình vẽ bên.
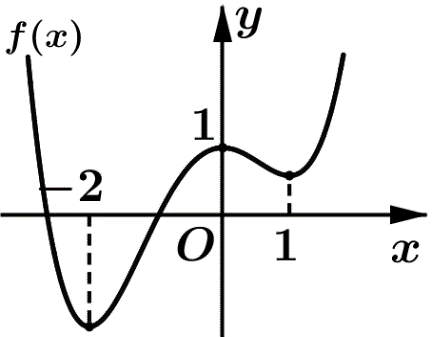
Hỏi hàm số \(y = f\left( |x + 1| - 3 \right)\) có bao nhiêu điểm cực trị?
A. \(3.\) B. \(5.\) C. \(6.\) D. \(7.\)
Hướng dẫn giải
Chọn D
Đồ thị hàm số \(y = f\left( |x + 1| - 3
\right)\) được suy từ đồ thị hàm số \(y
= f(x)\) bằng cách
• Tịnh tiến sang phải \(3\) đơn vị;
• Xóa bỏ phần đồ thị phía bên trái trục tung, phần đồ thị phía bên phải trục tung thì lấy đối xứng qua trục tung;
• Cuối cùng tịnh tiến đồ thị sang trái 1 đơn vị.
Ví dụ 3. Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ:
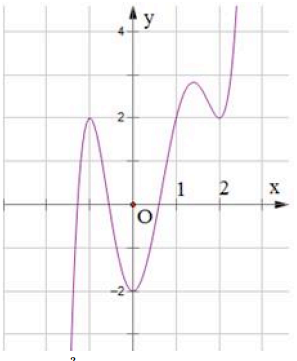
Đồ thị hàm số \(y = \left| 2f(x) - 3
\right|\) có bao nhiêu điểm cực trị?
A. \(4\). B. \(7\). C. \(5\). D. \(9\).
Hướng dẫn giải
Chọn B
Số điểm cực trị của hàm số \(y = \left|
2f(x) - 3 \right|\) bằng số điểm cực trị của hàm số \(y = \left| f(x) - \frac{3}{2}
\right|\).
Đồ thị của hàm số \(y = f(x) -
\frac{3}{2}(C)\) được suy ra từ đồ thị ban đầu bằng cách tịnh tiến theo trục \(Oy\) xuống dưới \(\frac{3}{2}\) đơn vị.
Đồ thị hàm số \(y = \left| f(x) -
\frac{3}{2} \right|\) được suy ra từ \((C)\) bằng cách giữ nguyên phần của \((C)\) bên trên trục hoành; lấy đối xứng qua \(Ox\) phần của \((C)\) dưới trục \(Ox\).
Dựa vào đồ thị suy ra số điểm cực trị là 7.
Ví dụ 4. Cho hàm số \(y = f(x)\) có bảng biến thiên như hình vẽ:
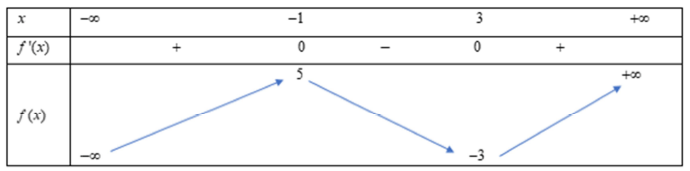
Hàm số \(y = \left| f(1 - 3x) + 1
\right|\) có bao nhiêu điểm cực trị?
A. \(2\). B. \(3\). C. \(4\). D. \(5\).
Hướng dẫn giải
Chọn D
Đặt \(g(x) = f(1 - 3x) + 1\) .
\(\Rightarrow g'(x) = - 3.f(1 -
3x)\) .
\(\Rightarrow g'(x) = 0 \Leftrightarrow
f(1 - 3x) = 0\) \(\Leftrightarrow
\left\lbrack \begin{matrix}
1 - 3x = - 1 \\
1 - 3x = 3
\end{matrix} \right.\ \Leftrightarrow \Leftrightarrow \left\lbrack
\begin{matrix}
x = \frac{2}{3} \\
x = - \frac{2}{3}
\end{matrix} \right.\)
Suy ra bảng biến thiên:
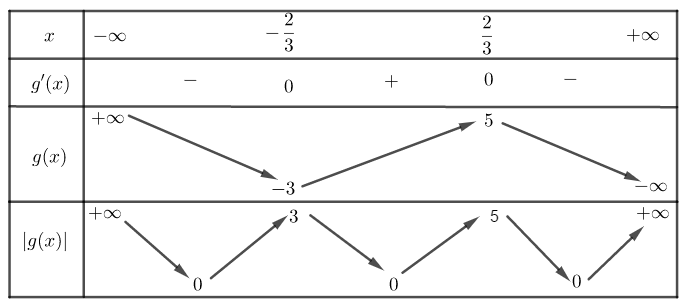
Vậy hàm số \(y = \left| g(x)
\right|\) có 5 điểm cực trị.
B. Bài tập tự rèn luyện tìm cực trị hàm trị tuyệt đối có đáp án chi tiết
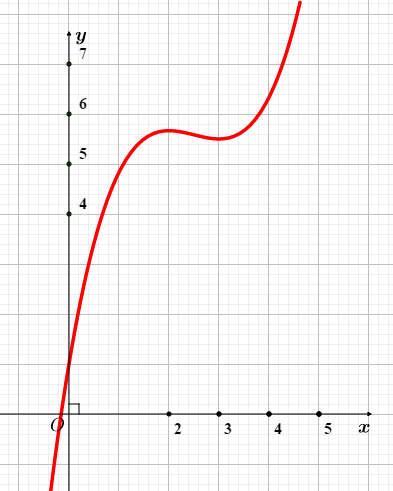
Bài tập 1. Cho \(y = f(x) =
\frac{1}{3}x^{3} - \frac{5}{2}x^{2} + 6x + 1\). Tìm số điểm cực trị của hàm số \(f\left( |x|
\right)\).
A. \(1\). B. \(2\). C. \(3\). D. \(5\).
Bài tập 2. Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ:
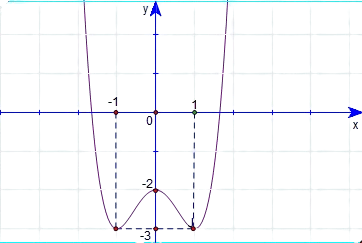
Hỏi đồ thị hàm số \(y = \left| f(x - 1) + 1
\right|\) có bao nhiêu điểm cực trị?
A. \(3\). B. \(4\). C. \(5\). D. \(7\).
Bài tập 3. Cho hàm số bậc ba \(y =
f(x)\) có đồ thị như hình vẽ.
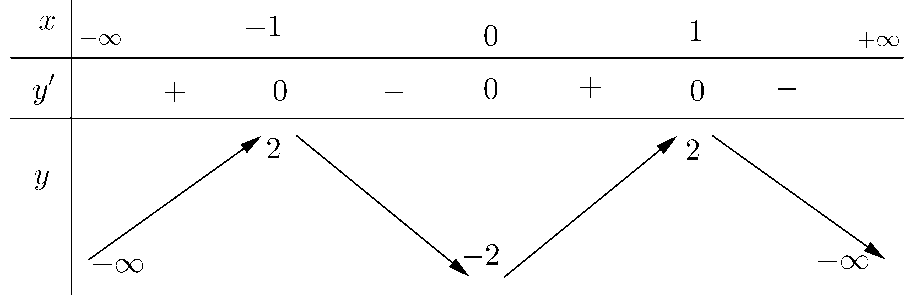
Hàm số \(y = \left| f\left( |x + 1| - 1
\right) \right|\) có bao nhiêu cực trị?
A. \(11\). B. \(7\). C. \(5\). D. \(6\).
Bài tập 4. Cho hàm số bậc bốn \(y = f(x)\) có bảng biến thiên như hình vẽ:
Số điểm cực trị của hàm số \(g(x) = \left|
f(x) + 1 \right|\) là:
A. \(10\). B. \(9\). C. \(8\). D. \(7\).
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
-------------------------------------------------------------
Với kiến thức và ví dụ cụ thể trong bài Tìm số cực trị của hàm trị tuyệt đối – Có đáp án, bạn đã nắm vững cách xác định số điểm cực trị nhanh chóng và chính xác. Đừng quên luyện tập thêm các bài tập vận dụng và tổng hợp cực trị hàm trị tuyệt đối để thành thạo kỹ năng này. Bạn có thể xem thêm các chuyên đề liên quan như biện luận cực trị, đạo hàm và ứng dụng đạo hàm, giúp củng cố toàn diện kiến thức Toán 12 và đạt điểm cao trong kỳ thi sắp tới.
