Tìm m để hàm số trị tuyệt đối có n cực trị Toán 12 có đáp án
Bài tập Toán 12: Cực trị của hàm trị tuyệt đối chứa tham số
Trong chương trình Toán 12, dạng toán tìm m để hàm số có n cực trị là dạng bài vận dụng cao, đòi hỏi học sinh hiểu sâu về tính liên tục, đạo hàm và cực trị của hàm trị tuyệt đối. Đặc biệt, khi hàm chứa tham số m, việc xác định số cực trị càng trở nên phức tạp do cần phân tích từng trường hợp biểu thức trong dấu giá trị tuyệt đối.
Bài viết Tìm m để hàm số trị tuyệt đối có n cực trị Toán 12 – Có đáp án chi tiết sẽ hướng dẫn bạn cách phân tích điều kiện cực trị, biện luận số cực trị theo m, kèm bài tập mẫu có lời giải cụ thể, giúp học sinh nắm chắc kiến thức, vận dụng thành thạo trong các đề thi THPT Quốc gia môn Toán và các bài luyện tập chuyên đề.
A. Ví dụ minh họa tìm m để hàm số trị tuyệt đối có cực trị
Ví dụ 1. Cho hàm số bậc bốn 
\(y =
f(x)\) có đồ thị hàm số như hình vẽ bên dưới:
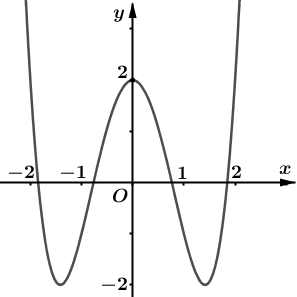
Số giá trị nguyên thuộc đoạn \(\lbrack -
10\ ;\ 10\rbrack\) của \(m\) để hàm số \(g(x) = \left| f(x) + m
\right|\) có đúng \(3\) điểm cực trị là:
A. \(10\). B. \(9\). C. \(8\). D. \(7\).
Hướng dẫn giải
Chọn B
Vì hàm \(f(x)\) đã cho có \(3\) điểm cực trị nên \(f(x) + m\) cũng luôn có \(3\) điểm cực trị.
Do đó, yêu cầu bài toán
\(\Leftrightarrow\) Phương trình \(f(x) + m = 0\) không có nghiệm đơn hoặc nghiệm bội lẻ
\(\Leftrightarrow\) Đồ thị \(y = f(x) + m\) là ảnh của đồ thị hàm số \(y = f(x)\) qua phép tịnh tiến lên trên ít nhất \(2\) đơn vị \(\Leftrightarrow m \geq 2.\)
Suy ra \(m = \left\{ 2;3;4;5;6;7;8;9;10
\right\}\)
Ví dụ 2. Cho đồ thị hàm số \(y =
f(x)\) có đồ thị như hình bên:
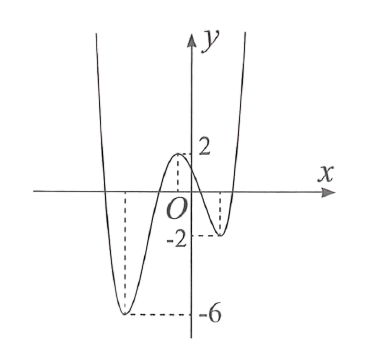
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y
= \left| f(x) - m + 1 \right|\) có \(7\) điểm cực trị?
A. \(2\). B. \(3\). C. \(4\). D. \(5\).
Hướng dẫn giải
Số cực trị của hàm số \(y = \left| f(x) - m
+ 1 \right|\) bằng tổng số cực trị của hàm số \(y = f(x)\) và số nghiệm đơn, bội lẻ của phương trình \(f(x) - m + 1 = 0\).
Do hàm số \(y = f(x)\) có \(3\) điểm cực trị, nên hàm số \(y = \left| f(x) - m + 1 \right|\) có \(7\) điểm cực trị \(\Leftrightarrow f(x) = m - 1\) có \(4\) nghiệm đơn bội lẻ
\(\Leftrightarrow - 2 < m - 1 < 2
\Leftrightarrow - 1 < m < 3\).
Vì \(m\) nguyên nên \(m = \left\{ 0;1;2 \right\}\). Vậy có \(3\) giá trị nguyên của \(m\).
Ví dụ 3. Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ bên:
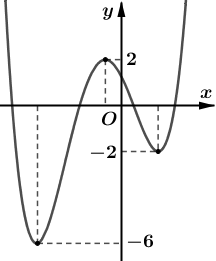
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(g(x) = \left| f(x + 2019) + m^{2} \right|\) có 5 điểm cực trị?
A. 1. B. 2. C. 3. D. 5.
Hướng dẫn giải
Chọn B
Vì hàm \(f(x)\) đã cho có \(3\) điểm cực trị nên \(f(x + 2019) + m^{2}\) cũng luôn có 3 điểm cực trị (do phép tịnh tiến không làm ảnh hưởng đến số cực trị).
Do đó yêu cầu bài toán \(\Leftrightarrow\) số giao điểm của đồ thị \(f(x + 2019) + m^{2}\) với trục hoành là 2.
Để số giao điểm của đồ thị \(f(x + 2019) +
m^{2}\) với trục hoành là 2, ta cần:
+ Tịnh tiến đồ thị \(f(x)\) xuống dưới tối thiểu 2 đơn vị \(\overset{}{\rightarrow}m^{2} \leq - 2:\) vô lý
+ Hoặc tịnh tiến đồ thị \(f(x)\) lên trên tối thiểu \(2\) đơn vị nhưng phải nhỏ hơn 6 đơn vị
\(\overset{}{\rightarrow}2
\leq m^{2} < 6 \Leftrightarrow \left\lbrack \begin{matrix}
\sqrt{2} \leq m < \sqrt{6} \\
- \sqrt{6} < m \leq - \sqrt{2}
\end{matrix} \right.\ \overset{m\mathbb{\in Z}}{\rightarrow}m \in
\left\{ - 2;2 \right\}.\)
Ví dụ 4. Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ bên dưới:
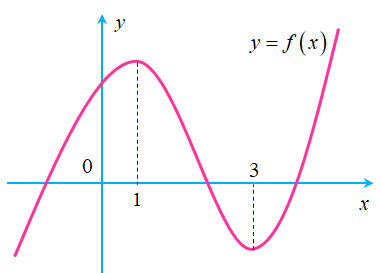
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(g(x) = f\left( |x + m| \right)\) có \(5\) điểm cực trị?
A. \(3.\) B. \(4.\) C. \(5.\) D. Vô số.
Hướng dẫn giải
Chọn D
Từ đồ thị hàm số ta thấy:
Hàm số \(f(x)\) có \(2\) điểm cực trị dương.
\(\overset{}{\rightarrow}f\left( |x|
\right)\) có \(5\) điểm cực trị.
\(\overset{}{\rightarrow}f\left( |x + m|
\right)\) có \(5\) điểm cực trị với mọi \(m\) (vì tịnh tiến sang trái hay sang phải không ảnh hưởng đến số điểm cực trị của hàm số).
Vậy có vô số giá trị \(m\) để hàm số \(g(x) = f\left( |x + m| \right)\) có \(5\) điểm cực trị.
B. Bài tập tự rèn luyện cực trị hàm trị tuyệt đối chứa tham số
Bài tập 1. Cho hàm số \(y = f(x)\) có bảng biến thiên như hình vẽ:
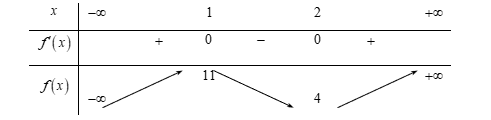
Tìm giá trị của \(m\) để đồ thị hàm số \(y = \left| f(x) - 2m \right|\) có \(5\) điểm cực trị.
A. \(m \in (4;11)\). B. \(m \in \left( 2;\frac{11}{2} \right)\). C. \(m = 3\). D. \(m \in \left\lbrack 2;\frac{11}{2}
\right\rbrack\).
Bài tập 2. Đường cong ở hình vẽ dưới đây là đồ thị của hàm số \(y = f(x)\).
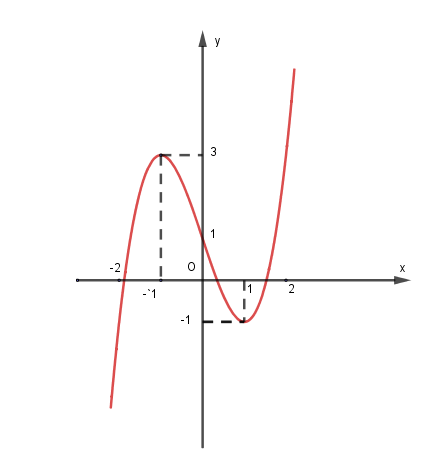
Tìm tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị hàm số \(y = f\left( |x + m| \right)\) có \(5\) điểm cực trị.
A. \(( - \infty; - 1\rbrack\). B. \((1; + \infty)\) . C. \(( - 1;1)\) . D. \(( - \infty; - 1)\).
Bài tập 3. Cho hàm số \(y = f(x)\) có đồ thị như hình vẽ sau:
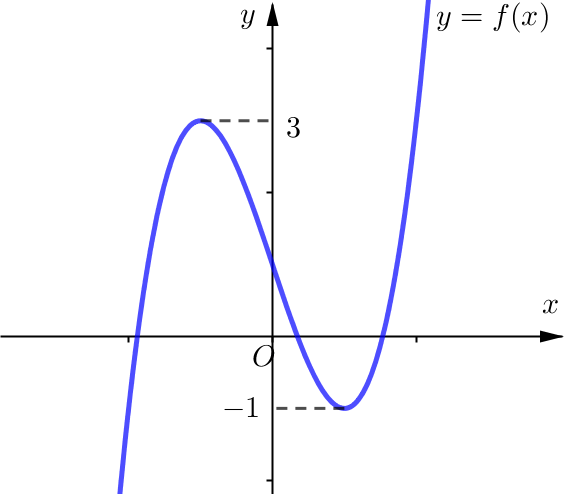
Có bao nhiêu số nguyên \(m \in \lbrack -
2019;\ 2019\rbrack\) sao cho hàm số \(y
= \left| f(x) + m \right|\) có ba điểm cực trị?
A. \(2017\). B. \(2019\). C. \(4036\). D. \(4038\).
Bài tập 4. Cho hàm số bậc ba \(y =
f(x)\) có đồ thị như hình bên:
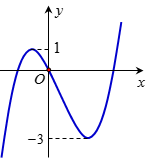
Tất cả các giá trị của tham số \(m\) để hàm số \(y = \left| f(x) + m
\right|\) có ba điểm cực trị là.
A. \(m = - 1\) hoặc \(m = 3\). B. \(1
\leq m \leq 3\).
C. \(m \leq - 1\) hoặc \(m \geq 3\). D. \(m \leq - 3\) hoặc \(m \geq 1\).
Bài tập 5. Cho hàm số bậc ba: \(f(x) =
ax^{3} + bx^{2} + cx + d,\left( a \neq 0,\ a,\ b,\ c,\ d\mathbb{\in R}
\right)\) có đồ thị như hình bên:
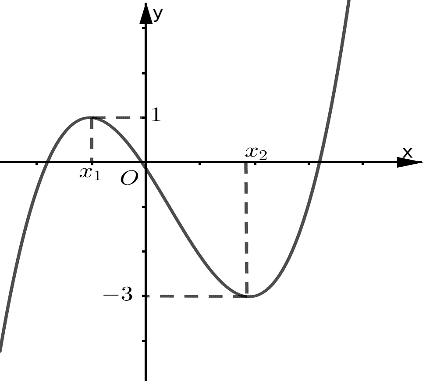
Tập tất cả các giá trị của tham số \(m\) để hàm số \(y
= \left| f(x) + m \right|\) có đúng ba điểm cực trị là
A. \(S = \left\{ - 1\ ;\ 3
\right\}\). B. \(S = \lbrack 1\ ;\
3\rbrack\).
C. \(S = ( - \infty\ ;\ \ - 1\rbrack \cup
\lbrack 3\ ;\ \ + \infty)\). D. \(S =
( - \infty\ ;\ - 3\rbrack \cup \lbrack 1\ ;\ + \infty)\).
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
------------------------------------------------------------
Thông qua bài viết Tìm m để hàm số trị tuyệt đối có n cực trị Toán 12, bạn đã nắm vững phương pháp xét đạo hàm, chia miền và biện luận số cực trị theo tham số m. Đây là kỹ năng quan trọng giúp học sinh xử lý nhanh các câu hỏi vận dụng cao trong đề thi THPT Quốc gia.
Hãy luyện tập thêm các dạng bài liên quan như biện luận cực trị của hàm trị tuyệt đối, ứng dụng đạo hàm trong khảo sát hàm số, và các bài toán cực trị có tham số, để hoàn thiện kỹ năng giải toán của mình. Đừng quên theo dõi thêm nhiều chuyên đề hữu ích khác trong mục Cực trị Toán 12 có đáp án để ôn thi hiệu quả hơn nhé!
