VnDoc.com Lớp 12 Toán 12 Giải Toán 12 nâng cao

Giải bài tập Toán 12 Nâng cao: Bài tập trắc nghiệm khách quan Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

Giải sgk Toán 12 Nâng cao: Bài tập trắc nghiệm khách quan Chương 1
1 324
Bài viết đã được lưu

Giải bài tập Toán 12 Nâng cao: Bài tập trắc nghiệm khách quan Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số hướng dẫn các em giải các bài tập trong sách giáo khoa, giúp các em củng cố và nắm vững kiến thức môn Toán 12.

Giải bài tập SGK Toán 12 Nâng cao: Bài tập trắc nghiệm khách quan Chương 1

Giải bài 80 sgk Toán 12 Nâng cao Đại số và Giải Tích

Hàm số \frac{x^3}{3}-\frac{x^2}{2}-6x+\frac{3}{4}

(A) Đồng biến trên khoảng (−2;3)

(B) Nghịch biến trên khoảng (−2;3)

(C) Nghịch biến trên khoảng (−∞;−2)

(D) Đồng biến trên khoảng (−2;+∞)

Giải

f′(x)=x2−x−6; f′(x)=0⇔ x=−2 và x=3

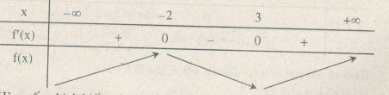
Giải sgk Toán 12 Nâng cao bài 80

(B) Nghịch biến trên khoảng (−2;3) Chọn (B).

Giải bài 81 sgk Toán 12 Nâng cao Đại số và Giải Tích

Hàm số f(x)= 6x5−15x4+10x3−22

(A) Nghịch biến trên R;

(B) Đồng biến trên khoảng (−∞;0) và nghịch biến trên khoảng (0;+∞)

(C) Đồng biến trên khoảng R

(D) Nghịch biến trên khoảng (0;1).

Giải

f′(x)= 30x4−60x3+30x2 =30x2(x2−2x+1)=30x2(x−1)2≥0

f ′ ( x ) = 0 ⇔ [ x = 0 x = 1

Hàm số đồng biến trên R. Chọn C.

Giải bài 82 sgk Toán 12 Nâng cao Đại số và Giải Tích

Hàm số y= sinx−x

(A) Đồng biến trên R.

(B) Đồng biến trên khoảng (−∞;0)

(C) Nghịch biến trên khoảng (−∞;0) và đồng biến trên khoảng (0;+∞)

(D) Nghịch biến trên R.

Giải

y′= cosx−1≤ 0 ∀ x ∈ R. Dấu bằng xảy ra khi và chỉ khi x= 2kπ

Hàm số nghịch biến trên R. Chọn D.

Giải bài 83 sgk Toán 12 Nâng cao Đại số và Giải Tích

Hàm số f(x)= x3−3x2−9x+11

(A) Nhận điểm x = -1 làm điểm cực tiểu;

(B) Nhận điểm x = 3 làm điểm cực đại;

(C) Nhận điểm x = 1 làm điểm cực đại;

(D) Nhận điểm x = 3 làm điểm cực tiểu.

Giải

f′(x)=3x2−6x−9

f′(x)=0⇔x=−1 và x=3

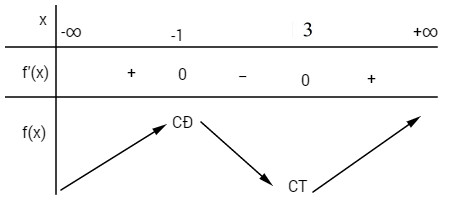
Giải sgk Toán 12 Nâng cao bài 83

Hàm số đạt cực tiểu tại điểm x = 3. Chọn D.

Giải bài 84 sgk Toán 12 Nâng cao Đại số và Giải Tích

Hàm số y=x4−4x3−5

(A) Nhận điểm x = 3 làm điểm cực tiểu.

(B) Nhận điểm x = 0 làm điểm cực đại

(C) Nhận điểm x = 3 làm điểm cực đại

(D) Nhận điểm x = 0 làm điểm cực tiểu.

Giải

y′= 4x3−12x2= 4x2(x−3)

y′=0⇔x=0 và x=3

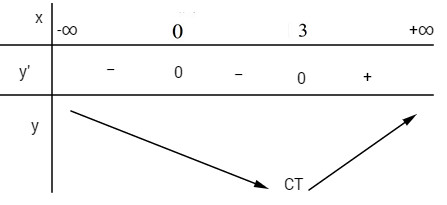
Giải sgk Toán 12 Nâng cao bài 84

Hàm số đạt cực tiểu tại điểm x = 3. Chọn A.

Giải bài 85 sgk Toán 12 Nâng cao Đại số và Giải Tích

Số điểm cực trị của hàm số y= x4−2x2−3 là

A) 0 (B) 1 (C) 3 (D) 2.

Giải

y′= 4x3−4x= 4x(x2−1)

y′=0⇔ x=0; x=1; x=−1

Hàm số đạt 3 cực trị. Chọn C.

Giải bài 86 sgk Toán 12 Nâng cao Đại số và Giải Tích

Số điểm cực trị của hàm số \frac{x^2-3x+6}{x-1} là

(A) 0 (B) 2 (C) 1 (D) 3.

Giải

y'=\ 1-\frac{4}{\left(x-1\right)^2}

y′=0⇔(x−1)2= 4⇔x=3 và x=−1

Hàm số có 2 cực trị. Chọn B.

Giải bài 87 sgk Toán 12 Nâng cao Đại số và Giải Tích

Hàm số f có đạo hàm là f′(x)=x2(x+1)2(2x−1)

Số điểm cực trị của hàm số là

(A) 1 (B) 2 (C) 0 (D) 3.

Giải

Vì x2(x+1)2≥0 ∀ x∈ R nên f’(x) chỉ đổi dấu khi x qua \frac{1}{2}

Hàm số có 1 cực trị. Chọn A.

Giải bài 88 sgk Toán 12 Nâng cao Đại số và Giải Tích

Hàm số y= x−sin2x+3

(A) Nhận điểm x=\frac{−\pi}{6} làm điểm cực tiểu.

(B) Nhận điểm x= \frac{\pi}{2} làm điểm cực đại.

(C) Nhận điểm x=\frac{-\pi}{6} làm điểm cực đại.

(D) Nhận điểm x=\frac{-\pi}{2} làm điểm cực tiểu.

Giải

y′=1−2cos2x; y′′= 4sin2x

Ta có: y′(\frac{−\pi}{6})= 0 và y′′(\frac{−\pi}{6})< 0

Hàm số nhận điểm x=\frac{−\pi}{6} làm điểm cực đại.

Chọn (C)

Giải bài 89 sgk Toán 12 Nâng cao Đại số và Giải Tích

Giá trị lớn nhất của hàm số -\sqrt{\left(3^{2^{^{ }}}+4^2\right)}=-5 và y= -3\sqrt{\left(1-x\right)}

(A) -3 (B) 1 (C) -1 (D) 0

Giải

y≤0, ∀x≤1 và y(1) = 0

Nên max y = 0

Chọn D

Giải bài 90 sgk Toán 12 Nâng cao Đại số và Giải Tích

Giá trị nhỏ nhất của hàm số y= 3sinx−4cosx là:

(A) 3 (B) -5 (C) -4 (D) -3.

Giải

Ta có -\sqrt{\left(a^{2^{^{ }}}+b^2\right)} ≤ asinx + bcosx ≤\sqrt{\left(a^2+b^2\right)}

Giá trị nhỏ nhất của 3sinx−4cosx là −\sqrt{\left(3^2+4^2\right)}=-5

Chọn B

Giải bài 91 sgk Toán 12 Nâng cao Đại số và Giải Tích

f(x)= g(x)⇔ 3-\frac{1}{x}=4x^2⇔ 4x3−3x+1=0⇔(2x−1)2(x+1)=0

f′(\frac{1}{2})=g′(\frac{1}{2})=0

f(x)=2x3+3x2−12x+2 trên đoạn [−1;2] là:

(A) 6 (B) 10 (C) 15 (D) 11.

Giải

f′(x)=6x2+6x−12

f′(x)=0⇔ x=1∈[−1;2] và x=−2∈[−1;2]

f(−1)=15; f(1)=−5; f(2)=6

Vậy max f(x)=15 Chọn C

Giải bài 92 sgk Toán 12 Nâng cao Đại số và Giải Tích

Giá trị lớn nhất của hàm số f(x)=\sqrt{\left(-x^2-2x+3\right)} là

(A) 2; (B) (C) 0; (D) 3.

Giải

TXĐ: D=[−3;1]

f′(x)= \frac{−2x−2}{2\sqrt{\left(−x^2−2x+3\right)}} = \frac{-\left(x+1\right)}{\sqrt{\left(−x^2−2x+3\right)}}

f′(0)⇔ x=−1 f(−1)=2

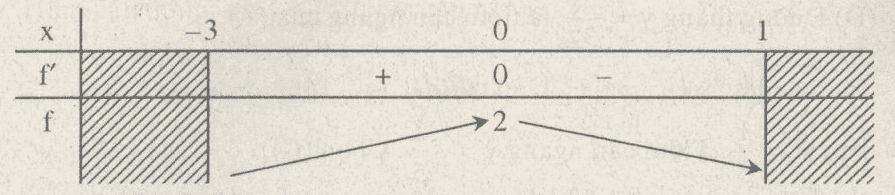
Giải sgk Toán 12 Nâng cao bài 92

Vậy max f(x)=2. Chọn (A).

Giải bài 93 sgk Toán 12 Nâng cao Đại số và Giải Tích

Gọi (C) là đồ thị của hàm số y=\frac{2x^2-3x+4}{2x+1}

(A) Đường thẳng x = -1 là tiệm cận đứng của (C).

(B) Đường thẳng x = 2x - 1 là tiệm cận đứng của (C).

(C) Đường thẳng x = x + 1 là tiệm cận đứng của (C).

(D) Đường thẳng x = x - 2 là tiệm cận đứng của (C).

Giải

y= x-2+\frac{6}{2x+1}

Tiệm cận xiên : y = x- 2. Chọn (D).

Giải bài 94 sgk Toán 12 Nâng cao Đại số và Giải Tích

Gọi (C) là đồ thị của hàm số y= \frac{x^2+3}{3+5x-2x^2}

(A) Đường thẳng x = 1 là tiệm cận đứng của đồ thị (C).

(B) Đường thẳng x=\frac{-1}{2} là tiệm cận đứng của đồ thị (C).

(C) Đường thẳng y = 1 là tiệm cận ngang của đồ thị (C).

(D) Đường thẳng x = -x +1 là tiệm cận xiên của đồ thị (C).

Giải

3+5x−2x2= 0⇔ x= \frac{-1}{2} và x= 3

Tiệm cận đứng x= \frac{-1}{2} Chọn (B).

Giải bài 95 sgk Toán 12 Nâng cao Đại số và Giải Tích

Gọi (C) là đồ thị của hàm số y=\frac{x^2+x+2}{-5x^2-2x+3}

(A) Đường thẳng x = 2 là tiệm cận đứng của (C).

(B) Đường thẳng y = x -1 là tiệm cận xiên của (C).

(C) Đường thẳng y=\frac{-1}{5} là tiệm cận ngang của (C).

(D) Đường thẳng y=\frac{-1}{2} là tiệm cận ngang của (C).

Giải

lim (x→±∞) y= \frac{1}{5} Tiệm cận ngang y=\frac{-1}{5}. Chọn (C).

Giải bài 96 sgk Toán 12 Nâng cao Đại số và Giải Tích

Đồ thị của hàm số y= x+\frac{1}{x-1}

(A) cắt đường thẳng y = 1 tại hai điểm

(B) cắt đường thẳng y = 4 tại hai điểm

(C) Tiếp xúc với đường thẳng y = 0.

(D) Không cắt đường thẳng y = -2.

Giải

x+\frac{1}{x-1}=4 <=> x2−x+1= 4x−4⇔ x2−5x+5=0 (1)

(1) Có hai nghiệm phân biệt. Chọn (B).

Giải bài 97 sgk Toán 12 Nâng cao Đại số và Giải Tích

Xét phương trình x3+3x2=m

(A) Với m =5, phương trình đã có ba nghiệm

(B) Với m = -1, phương trình có hai nghiệm.

(C) Với m =4, phương trình đã có ba nghiệm phân biệt

(D) Với m =2, phương trình đã có ba nghiệm phân biệt

Giải

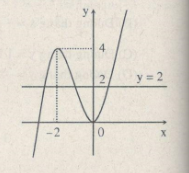
Giải sgk Toán 12 Nâng cao bài 97

Vẽ đồ thị hàm số y=x3+3x2

y′=3x2+6x; y′=0⇔x=-2; y(-2)=4 và x=0; y(0)= 0

m =2: Phương trình có 3 nghiệm phân biệt.

Chọn (D).

Giải bài 98 sgk Toán 12 Nâng cao Đại số và Giải Tích

Đồ thị hàm số y=\frac{x-2}{2x+1}

(A) Nhận điểm \left(\frac{-1}{2};\frac{1}{2}\right) làm tâm đối xứng.

(B) Nhận điểm \left(\frac{-1}{2};\ 2\right) làm tâm đối xứng.

(C) Không có tâm đối xứng.

(D) Nhận điểm \left(\frac{1}{2};\frac{1}{2}\right) làm tâm đối xứng.

Giải

Tiệm cận đứng: x=\frac{-1}{2}; Tiệm cận ngang: y=\frac{-1}{2}

Giao điểm hai tiệm cận I\left(\frac{-1}{2};\frac{1}{2}\right) là tâm đối xứng của đồ thị hàm số.

Chọn (A).

Giải bài 99 sgk Toán 12 Nâng cao Đại số và Giải Tích

Số giao điểm của hai đường cong y=x3−x2−2x+3 và y= x2−x+1 là:

(A) 0 (B) 1 (C) 3 (D) 2.

Giải

Hoành độ giao điểm của hai đường cong là nghiệm phương trình:

x3−x2−2x+3=x2−x+1⇔x3−2x2−x+2=0⇔(x−1)(x2−x−2)=0

⇔(x−1)(x+1)(x−2)=0 ⇔ x=±1 và x= 2 Chọn C

Giải bài 100 sgk Toán 12 Nâng cao Đại số và Giải Tích

Các đồ thị của hai hàm số y=3-\frac{1}{x} và y=4x2 tiếp xúc với nhau tại điểm M có hoành độ là:

(A) x = -1 (B) x = 1 (C) x =2 (D) x=\frac{1}{2}

Giải

f(x)=g(x)⇔3-\frac{1}{x}=4x^2⇔4x3−3x+1=0⇔(2x−1)2(x+1)=0

f'\left(\frac{1}{2}\right)=g'\left(\frac{1}{2}\right)=0

Chọn (D).

Tài liệu giúp các em hệ thống lại những kiến thức đã học với những câu hỏi đa dạng bám sát lí thuyết các em đã học. Các em có thể tự học bài ở nhà và chuẩn bị kiến thức cho những kiến thức cho những kì thi quan trọng. Các em có thể tham khảo thêm Giải bài tập Toán 12 Nâng cao để mở rộng kiến thức.

VnDoc xin giới thiệu tới các em Giải bài tập Toán 12 Nâng cao: Bài tập trắc nghiệm khách quan Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số. Hi vọng tài liệu sẽ giúp các em có thêm những phương pháp giải bài tập thật hiệu quả để đạt hiệu quả cao trong quá trình làm bài. Các em có thể tham khảo thêm các tài liệu khác tại mục Tài liệu học tập lớp 12 do VnDoc tổng hợp và đăng tải như: Trắc nghiệm Tiếng Anh 12, Trắc nghiệm Hóa học 12, Trắc nghiệm Sinh học 12,....

Đánh giá bài viết
1 324
Tìm thêm: Giải bài tập Toán 12 Nâng cao bài tập trắc nghiệm khách quan chương 1 giải sgk toán 12 nâng cao bài tập trắc nghiệm khách quan chương 1 giải toán 12 sgk nâng cao
Sắp xếp theo
Xóa Đăng nhập để Gửi
    Giải bài tập Toán SGK 12 Nâng cao

    Tham khảo thêm

    Giải Toán 12 nâng cao

    Xem thêm