VnDoc.com

Tiệm cận ngang của đồ thị hàm số

Cách tìm tiệm cận ngang Toán 12

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Phân loại: Tài liệu Tính phí

Tiệm cận ngang Toán 12

1. Tiệm cận ngang
2. Cách tìm tiệm cận ngang của đồ thị hàm số
3. Bài tập tìm tiệm cận ngang của đồ thị hàm số

Để giúp các bạn học sinh lớp 12 học tập tốt hơn môn Toán, VnDoc xin mời các bạn tham khảo tài liệu Cách tìm tiệm cận. Bộ tài liệu hướng dẫn chi tiết về tiệm cận ngang, cách tìm tiệm cận ngang của đồ thị hàm số cho trước được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và đề thi THPT Quốc gia. Hi vọng tài liệu này sẽ giúp các bạn ôn thi THPT Quốc gia môn Toán trắc nghiệm hiệu quả.

Cách tìm tiệm cận ngang Toán 12

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

1. Tiệm cận ngang

- Cho đồ thị hàm số $y = f\left( x \right)$ $y = f\left( x \right)$ có tập xác định D.

- Nếu $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}$ $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}$ hoặc $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}$ $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}$ thì đường thẳng $y = {y_0}$ $y = {y_0}$ được gọi là tiệm cận ngang của đồ thị hàm số.

2. Cách tìm tiệm cận ngang của đồ thị hàm số

Phương pháp giải

Bước 1. Tìm tập xác định của hàm số.

Bước 2. Tính các giới hạn của hàm số đó tại vô cực (nếu có). Từ đó xác định đường tιệm cận ngang.

Công thức tính tiệm cận ngang của hàm phân thức hữu tỉ:

Hàm số		Tiệm cận ngang
$y = \frac{{{a_0}{x^m} + {a_1}{x^{m - 1}} + ... + {a_m}}}{{{b_0}{x^n} + {b_1}{x^{n - 1}} + ... + {b_m}}}$ $y = \frac{{{a_0}{x^m} + {a_1}{x^{m - 1}} + ... + {a_m}}}{{{b_0}{x^n} + {b_1}{x^{n - 1}} + ... + {b_m}}}$ ${a_0} \ne 0,{b_0} \ne 0;m \geqslant 1;n \geqslant 1;m,n \in \mathbb{Z}$ ${a_0} \ne 0,{b_0} \ne 0;m \geqslant 1;n \geqslant 1;m,n \in \mathbb{Z}$	m = n	$y = \frac{{{a_0}}}{{{b_0}}}$ $y = \frac{{{a_0}}}{{{b_0}}}$
	m > n	Không có tiệm cận ngang
	m < n	y = 0

Công thức tính tiệm cận ngang của hàm phân thức vô tỷ:

Hàm số		Tiệm cận ngang
$y = \frac{{ax + b}}{{\sqrt {c{x^2} + dx + e} }}$ $y = \frac{{ax + b}}{{\sqrt {c{x^2} + dx + e} }}$	c < 0	Không có tiệm cận ngang
$a,c \ne 0$ $a,c \ne 0$	c > 0	$y = \pm \frac{a}{{\sqrt c }}$ $y = \pm \frac{a}{{\sqrt c }}$

3. Bài tập tìm tiệm cận ngang của đồ thị hàm số

Bài tập 1: Tìm tiệm cận ngang của đồ thị hàm số: $y = \frac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}}$ $y = \frac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}}$

Hướng dẫn giải

$\begin{matrix} \mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}} = \dfrac{3}{2} \hfill \\ \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}} = \dfrac{{ - 1}}{2} \hfill \\ \end{matrix}$ $\begin{matrix} \mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}} = \dfrac{3}{2} \hfill \\ \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}} = \dfrac{{ - 1}}{2} \hfill \\ \end{matrix}$

Vậy $y = \frac{3}{2};y = \frac{{ - 1}}{2}$ $y = \frac{3}{2};y = \frac{{ - 1}}{2}$ là tiệm cận ngang của đồ thị hàm số.

Bài tập 2: Cho hàm số $y = \frac{{x - 1}}{{\sqrt {{x^2} - 3x + 2} }}$ $y = \frac{{x - 1}}{{\sqrt {{x^2} - 3x + 2} }}$ có đồ thị (C). Tìm khẳng định đúng trong các khẳng định sau:

A. (C) có đúng một tiệm cận ngang y = 1

B. (C) có đúng một tiệm cận ngang y = -1

C. (C) không có tiệm cận ngang

D. (C) có hai tiệm cận ngang là y = 1 và y = -1

Hướng dẫn giải

$\begin{matrix} \mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 - \frac{1}{x}}}{{\sqrt {1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}} }} = 1 \hfill \\ \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{1 - \dfrac{1}{x}}}{{\sqrt {1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}} }} = - 1 \hfill \\ \end{matrix}$ $\begin{matrix} \mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 - \frac{1}{x}}}{{\sqrt {1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}} }} = 1 \hfill \\ \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{1 - \dfrac{1}{x}}}{{\sqrt {1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}} }} = - 1 \hfill \\ \end{matrix}$

Vậy y =1 và y = -1 là hai tiệm cận ngang của đồ thị hàm số (C)

Đáp án D

Bài tập 3: Cho đồ thị hàm số $y = \sqrt {m{x^2} + 2x} - x$ $y = \sqrt {m{x^2} + 2x} - x$. Tìm tất cả giá trị tham số m để đồ thị hàm số có tiệm cận ngang.

A. $m > 0$	B. $m = - 2$
C. $m = \pm 1$ $m = \pm 1$	D. $m = \left\{ {1; - 2} \right\}$ $m = \left\{ {1; - 2} \right\}$

Hướng dẫn giải

Ta có: $y = \sqrt {m{x^2} + 2x} - x = \frac{{m{x^2} + 2x - {x^2}}}{{\sqrt {m{x^2} + 2x} + x}} = \frac{{\left( {m - 1} \right){x^2} + 2x}}{{\sqrt {m{x^2} + 2x} + x}}$ $y = \sqrt {m{x^2} + 2x} - x = \frac{{m{x^2} + 2x - {x^2}}}{{\sqrt {m{x^2} + 2x} + x}} = \frac{{\left( {m - 1} \right){x^2} + 2x}}{{\sqrt {m{x^2} + 2x} + x}}$

Đồ thị hàm số có tiệm cận ngang khi và chỉ khi bậc của tử bé hơn bậc của mẫu và tồn tại

$\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {m - 1 = 0} \end{array} \Leftrightarrow m = 1} \right.$ $\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {m - 1 = 0} \end{array} \Leftrightarrow m = 1} \right.$

Đáp án A

Bài tập 4: a. Đồ thị hàm số $y = \frac{x - 3}{6 - 3x}$ $y = \frac{x - 3}{6 - 3x}$ có bao nhiêu tiệm cận đứng và tiệm cận ngang?

b. Xác định số đường tiệm cận ngang của đồ thị hàm số $y = \frac{x}{\sqrt{x^{2} + 1}}$ $y = \frac{x}{\sqrt{x^{2} + 1}}$?

Hướng dẫn giải

a. Ta có: $\lim_{x \rightarrow \pm \infty}y = \lim_{x \rightarrow \pm \infty}\frac{x - 3}{6 - 3x} = - \frac{1}{3}$ $\lim_{x \rightarrow \pm \infty}y = \lim_{x \rightarrow \pm \infty}\frac{x - 3}{6 - 3x} = - \frac{1}{3}$ nên đường thẳng $y = - \frac{1}{3}$ $y = - \frac{1}{3}$ là tiệm cận ngang của đồ thị hàm số.

$\left\{ \begin{matrix} \lim_{x \rightarrow 2^{+}}y = \lim_{x \rightarrow 2^{+}}\frac{x - 3}{6 - 3x} = + \infty \\ \lim_{x \rightarrow 2^{-}}y = \lim_{x \rightarrow 2^{-}}\frac{x - 3}{6 - 3x} = - \infty \\ \end{matrix} \right.$ $\left\{ \begin{matrix} \lim_{x \rightarrow 2^{+}}y = \lim_{x \rightarrow 2^{+}}\frac{x - 3}{6 - 3x} = + \infty \\ \lim_{x \rightarrow 2^{-}}y = \lim_{x \rightarrow 2^{-}}\frac{x - 3}{6 - 3x} = - \infty \\ \end{matrix} \right.$ nên đường thẳng $x = 2$ là tiệm cận đứng của đồ thị hàm số.

Vậy đồ thị hàm số có số tiệm cận đứng và tiệm cận ngang là 2.

b. Ta có:

$\lim_{x \rightarrow + \infty}y = \lim_{x \rightarrow + \infty}\left( \frac{x}{\sqrt{x^{2} + 1}} \right) = 1$ $\lim_{x \rightarrow + \infty}y = \lim_{x \rightarrow + \infty}\left( \frac{x}{\sqrt{x^{2} + 1}} \right) = 1$ suy ra $y = 1$ là một tiệm cận ngang của đồ thị hàm số.

$\lim_{x \rightarrow - \infty}y = \lim_{x \rightarrow - \infty}\left( \frac{x}{\sqrt{x^{2} + 1}} \right) = - 1$ $\lim_{x \rightarrow - \infty}y = \lim_{x \rightarrow - \infty}\left( \frac{x}{\sqrt{x^{2} + 1}} \right) = - 1$ suy ra $y = - 1$ là một tiệm cận ngang của đồ thị hàm số.

Vậy tổng số đường tiệm cận ngang của đồ thị hàm số đã cho bằng 2.

Bài tập 5. Đường thẳng $y = - 2$ là đường tiệm cận của đồ thị hàm số nào sau đây?

A. $y = \frac{2}{3x + 2}$ $y = \frac{2}{3x + 2}$ B. $y = \frac{2x^{3} - 3}{x + 2}$ $y = \frac{2x^{3} - 3}{x + 2}$

C. $y = \frac{2x^{2} + x - 1}{(x + 1)(3 - x)}$ $y = \frac{2x^{2} + x - 1}{(x + 1)(3 - x)}$ D. $y = \frac{\sqrt{x^{2} + 1}}{2x - 1}$ $y = \frac{\sqrt{x^{2} + 1}}{2x - 1}$

Hướng dẫn giải

$y = \frac{2}{3x + 2}$ $y = \frac{2}{3x + 2}$ có $\lim_{x \rightarrow \infty}y = 0$ $\lim_{x \rightarrow \infty}y = 0$ suy ra $y = 0$ là tiệm cận ngang của đồ thị hàm số. (Loại)

$y = \frac{2x^{3} - 3}{x + 2}$ $y = \frac{2x^{3} - 3}{x + 2}$ có $\lim_{x \rightarrow \infty}y = \infty$ $\lim_{x \rightarrow \infty}y = \infty$ nên đồ thị hàm số không có tiệm cận ngang (loại)

$y = \frac{2x^{2} + x - 1}{(x + 1)(3 - x)} = \frac{2x^{2} + x - 1}{- x^{2} + 2x + 3}$ $y = \frac{2x^{2} + x - 1}{(x + 1)(3 - x)} = \frac{2x^{2} + x - 1}{- x^{2} + 2x + 3}$ có $\lim_{x \rightarrow \infty}y = - 2$ $\lim_{x \rightarrow \infty}y = - 2$ suy ra $y = - 2$ là tiệm cận ngang (Thỏa mãn).

Vậy đường thẳng $y = - 2$ là đường tiệm cận của đồ thị hàm số $y = \frac{2x^{2} + x - 1}{(x + 1)(3 - x)}$ $y = \frac{2x^{2} + x - 1}{(x + 1)(3 - x)}$.

Bài tập 6. Cho hàm số $y = \frac{(2m + 1)x^{2} + 3}{\sqrt{x^{4} + 1}}$ $y = \frac{(2m + 1)x^{2} + 3}{\sqrt{x^{4} + 1}}$ với $m$ là tham số. Tìm giá trị của $m$ để đường tiệm cận ngang của đồ thị hàm số đi qua điểm $A(1; - 3)$?

Hướng dẫn giải

Ta có: $\lim_{x \rightarrow + \infty}y = \lim_{x \rightarrow - \infty}y = 2m + 1$ $\lim_{x \rightarrow + \infty}y = \lim_{x \rightarrow - \infty}y = 2m + 1$ suy ra $d:y = 2m + 1$ là tiệm cận ngang của đồ thị hàm số đã cho.

Do $A(1; - 3) \in d \Leftrightarrow 2m + 1 = - 3 \Leftrightarrow m = - 2$ $A(1; - 3) \in d \Leftrightarrow 2m + 1 = - 3 \Leftrightarrow m = - 2$

Bài tập 7. Cho hàm số $y = f(x)$ có bảng biến thiên như sau:

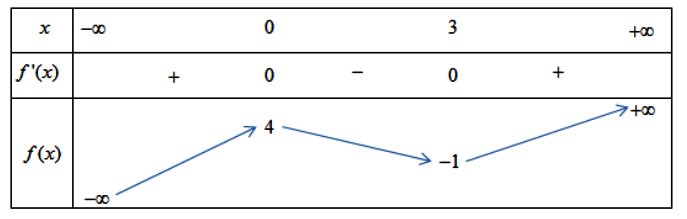
Mệnh đề nào sau đây đúng?

A. Đồ thị hàm số có hai đường tiệm cận ngang.

B. Đồ thị hàm số có đường tiệm cận ngang $y = 4$.

C. Đồ thị hàm số không có tiệm cận.

D. Đồ thị hàm số có đường tiệm cận đứng $x = 0$.

Hướng dẫn giải

Từ bảng biến thiên của hàm số $y = f(x)$ ta có: $\lim_{x \rightarrow - \infty}f(x) = - \infty;\lim_{x \rightarrow + \infty}f(x) = + \infty$ $\lim_{x \rightarrow - \infty}f(x) = - \infty;\lim_{x \rightarrow + \infty}f(x) = + \infty$ nên đồ thị hàm số đã cho không có tiệm cận ngang.

Và $\left\{ \begin{matrix} \lim_{x \rightarrow 0^{+}}f(x) = 4;\lim_{x \rightarrow 0^{-}}f(x) = 4 \\ \lim_{x \rightarrow 3^{-}}f(x) = - 1;\lim_{x \rightarrow 3^{+}}f(x) = - 1 \\ \end{matrix} \right.$ $\left\{ \begin{matrix} \lim_{x \rightarrow 0^{+}}f(x) = 4;\lim_{x \rightarrow 0^{-}}f(x) = 4 \\ \lim_{x \rightarrow 3^{-}}f(x) = - 1;\lim_{x \rightarrow 3^{+}}f(x) = - 1 \\ \end{matrix} \right.$ nên đồ thị hàm số đã cho không có tiệm cận đứng.

Vậy đồ thị hàm số đã cho không có tiệm cận.

Bài tập 8: Cho hàm số $y = \frac{2mx + m}{x - 1}$ $y = \frac{2mx + m}{x - 1}$. Tìm tất cả các giá trị thực của tham số $m$ để đường tiệm cận ngang của đồ thị hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng $8$.

Hướng dẫn giải

Điều kiện để đồ thị hàm số có tiệm cận là $- 2m - m \neq 0 \Leftrightarrow m \neq 0$ $- 2m - m \neq 0 \Leftrightarrow m \neq 0$

Khi đó đồ thị hàm số có:

Tiệm cận đúng: $x = 1$, song song với $Oy$ và cắt $Ox$ tại điểm $A(1;0)$

Tiệm cận ngang: $y = 2m$ song song với $Ox$ và cắt $Oy$ tại điểm $B(2m;0)$

Diện tích hình chữ nhật tạo bởi hai đường tiệm cận cùng với hai trục tọa độ là

$S = OA.OB = 1.|2m| = 8 \Leftrightarrow m = \pm 4$ $S = OA.OB = 1.|2m| = 8 \Leftrightarrow m = \pm 4$

--------------------------------------------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Tiệm cận Toán 12. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Thi THPT Quốc gia môn Toán.

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Ma Kết

1

1.416

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!