Hướng dẫn tìm GTLN, GTNN của hàm số lớp 12 bằng máy tính CASIO
Trong chương trình Toán 12, chuyên đề tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số là một phần không thể thiếu trong các đề thi THPT Quốc gia. Bên cạnh việc giải tự luận, sử dụng máy tính CASIO là một phương pháp nhanh, chính xác và cực kỳ hiệu quả để kiểm tra kết quả hoặc tìm đáp án trắc nghiệm. Trong bài viết này, chúng tôi sẽ hướng dẫn bạn cách sử dụng máy tính CASIO để tìm GTLN, GTNN của hàm số một cách chi tiết, dễ hiểu, giúp bạn tiết kiệm thời gian làm bài và nâng cao hiệu quả ôn thi.
Hướng dẫn tìm GTLN, GTNN của hàm số lớp 12 bằng máy tính CASIO
Các dạng toán tìm GTLN GTNN của hàm số lớp 12
Dạng 1: Tìm giá trị lớn nhất, nhỏ nhất của hàm số trên 1 đoạn
Bài toán: Tìm GTLN GTNN của hàm số y= f (x) trên miền [a;b]
Bước 1: Lập bảng giá trị trên máy tính Casio với lệnh MODE 7.
Bước 2: Nhập f(x) =…
Start?a= → End?b= → step?α =
α là ta chọn tùy thuộc vào đoạn trong đề bài
Ta nhận được bảng giá trị, quan sát sẽ thấy giá trị lớn nhất hiển thị là max, giá trị nhỏ nhất sẽ hiển thị là min.
Nếu trong đề bài có liên quan đến lượng giác như sinx, cosx… các em hãy chuyển máy tính sang chế độ radian bằng SHIEF MODE 4 và tính.
Ví dụ: Tìm GTLN GTNN của hàm số y = x3 + 3x2 trên đoạn [-1;3].
Hướng dẫn giải
Nhập MODE 7, nhập f(x)=x3 + 3x² Start?-1= End? 3= step? 0.5 =
Ta được bảng giá trị
| x | f(x) |
| -1 | 2 |
| -0.5 | 0.625 |
| 0 | 0 |
| 0.5 | 0.875 |
| 1 | 4 |
| 1.5 | 10.125 |
| 2 | 20 |
| 2.5 | 34.375 |
| 3 | 54 |
Từ bảng giá trị trên ta thấy f(3) = 54 là giá trị lớn nhất, f(0) = 0 là giá trị nhỏ nhất.
Dạng 2: Tìm GTLN GTNN của hàm số trên một khoảng
Các bước tìm giá trị lớn nhất, nhỏ nhất của dạng bài này cũng tương tự như dạng 1. Nhưng các em cần chú ý đề việc chọn GTLN, GTNN. Cần xem xét kĩ x có thuộc miền trong đề bài không.
Dạng 3: Tìm GTLN GTNN của hàm số có chứa tham số m
Các em hãy tham khảo cách sử dụng máy tính giải dạng toán này qua ví dụ sau:
Ví dụ 1: Giá trị lớn nhất của hàm số 
\(y = \frac{{2mx + 1}}{{m - x}}\) trên đoạn [2; 3] là \(- \frac{1}{3}\) khi m nhận giá trị bằng bao nhiêu?
| A. m = -5 | B. m = -1 |
| C. m = 0 | D. m = 1 |
Hướng dẫn giải:
Nếu hiểu giá trị nhỏ nhất của \(y = - \frac{1}{3}\) trên đoạn [2; 3] có nghĩa là phương trình \(y + \frac{1}{3} = 0\) có nghiệm thuộc đoạn [2; 3].
Thử nghiệm đáp án A với m = -5 ta thiết lập \(\frac{{ - 10x + 1}}{{ - 5 - x}} + \frac{1}{3} = 0\). Sử dụng chức nặng dò nghiệm SHIFT SOLVE
Ta thấy \(y = \frac{1}{3}\) thì \(x = - 0,064...\) không phải giá trị thuộc đoạn [2; 3] vậy đáp án A sai.
Tương tự như vậy ta thấy đáp án C đúng với m = 0 khi đó y có dạng \(\frac{1}{{ - x}}\)
Ta thấy khi \(y = \frac{1}{3}\) khi x = 3 là giá trị thuộc đoạn [2;3] suy ra C chính xác
Ví dụ 2. Một vật chuyển động theo quy luật \(S = - \frac{1}{2}{t^3} + 9{t^2}\) với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu, vận tốc lớn nhất của vật đạt được bằng bao nhiêu (đơn vị m/s)?
A. 216 B . 30 C. 400 D. 54
Hướng dẫn giải
Gọi hàm số của vận tốc là v = v(t). Quãng đường vật đi được tính theo công thức \(S = \int\limits_{{t_0}}^{{t_1}} {v\left( t \right)dt}\)
Hay ta hiểu \(s'\left( t \right) = v\left( t \right) \Rightarrow v\left( t \right) = - \frac{3}{2}{t^2} + 18t\)
Bài toán lúc này trở thành tìm giá trị lớn nhất của hàm số trên \(v\left( t \right) = - \frac{3}{2}{t^2} + 18t\)miền thời gian từ 0 đến 10 giây. Để làm việc này ta sử dụng tính năng lập bảng giá trị MODE 7 của Casio.
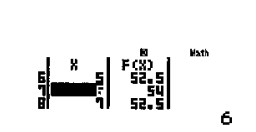
Quan sát bảng giá trị ta thấy giá trị lớn nhất xuất hiện là 54.
Đáp án cần tìm là đáp án D. 54.
Ví dụ 3. Gọi M, N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x) = \left( x^{2} - 3
\right)e^{x}\) trên đoạn \(\lbrack
0;2\rbrack\). Tính giá trị của biểu thức \(P = \left( m^{2} - 4M \right)^{2016}\)?
A. \(P = 0\) B. \(P = e^{2016}\) C. \(P = 1\) D. \(P = 2^{2016}\)
Hướng dẫn giải
Lập bảng giá trị cho \(f(x) = \left( x^{2}
- 3 \right)e^{x}\) với lệnh MODE 7 Start 0 End 2 Step \(\frac{2}{19}\) ta được:
Quan sát bảng giá trị ta thấy m = -5,422 và M = 7,389
Suy ra \(P = \left( m^{2} - 4M
\right)^{2016} = ( - 0,157919)^{2016} \approx 0\)
Vậy đáp án chính xác là đáp án A.
Ví dụ 4. Cho hàm số \(y = 3sinx -
4sin^{3}x\). Tính giá trị lớn nhất của hàm số đã cho trên khoảng \(\left( - \frac{\pi}{2};\frac{\pi}{2}
\right)\)?
A. 1 B. 7 C. -1 D. 3
Hướng dẫn giải
Lập bảng giá trị cho \(y = 3sinx -
4sin^{3}x\) với lệnh MODE 7 Start \(-
\frac{\pi}{2}\) End \(\frac{\pi}{2}\) Step \(\frac{\pi}{19}\) ta được:
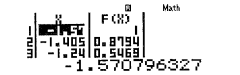
Quan sát bảng giá trị ta thấy giá trị lớn nhất là 1
Vậy đáp án chính xác là đáp án A.
Ví dụ 5. Xét các số thực a và b thỏa mãn a > b > 1. Tìm giá tri nhỏ nhất Pmin của biểu thức \(P =
log_{\frac{a}{b}}^{2}\left( a^{2} \right) + 3;log_{b}\left( \frac{a}{b}
\right)\).
A. \(P_{\min} = 19\) B. \(P_{\min} = 13\) C. \(P_{\min} = 14\) D. \(P_{\min} = 15\)
Hướng dẫn giải
Chọn b = 1.125 rồi sử dụng chức năng MODE 7 tìm min của biểu thức:
\(P = log_{\frac{a}{1,125}}^{2}\left(
a^{2} \right) + 3;log_{b}\left( \frac{a}{1,125} \right)\)
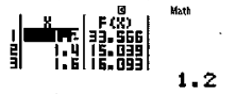
Ta thấy giá trị nhỏ nhất có thể xuất hiện là 15,039 gần với 15 nhất
=> Đáp số chính xác là D.
Ví dụ 6. Hàm số \(y = |3\cos x - 4\sin x +8|\) với \(x \in \lbrack
0;2\pi\rbrack\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Tính giá trị của biểu thức \(T = M + m\)?
A. \(T = 8\sqrt{2}\) B. \(T = 7\sqrt{3}\) C. \(T = 8\sqrt{3}\) D. \(T = 16\)
Hướng dẫn giải
Để tính toán các bài toán liên quan đến lượng giác ta chuyển máy tính về chế độ Radian
Sử dụng chức năng MODE 7 của máy tính casio với thiết lập Start 0 End \(2\pi\)Step \(\frac{2\pi - 0}{19}\)
Quan sát bảng giá trị F(X) ta thấy giá trị lớn nhất F(X) có thể đạt được là: \(f(5,2911) = 12,989 \approx 13 =
M\)
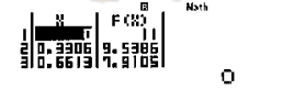
Ta thấy giá trị nhỏ nhất F(X) có thể đạt được là:
\(f(2,314) = 3,0252 \approx 3 =
m\)
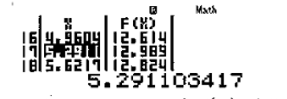
Vậy \(T = M + m = 16\). Vậy đáp án chính xác là D.
Ví dụ 7. Cho các số x, y thỏa mãn điều kiện \(y \leq 0;x^{2} + x - y - 12 = 0\). Tính giá trị nhỏ nhất của biểu thức \(P = xy + x + 2y +
17\).
A. \(P_{\min} = - 12\) B. \(P_{\min} = - 9\) C. \(P_{\min} = - 15\) D. \(P_{\min} = - 5\)
Hướng dẫn giải
Cách 1: Từ \(x^{2} + x - y - 12 =
0\) ta biến đổi được thành \(y = x^{2}
+ x - 12\).
Thay vào P ta được:
\(P = (x + 2)\left( x^{2} + x - 12 \right)
+ x + 17\).
Để tìm min của P ta sử dụng chức năng MODE 7 của máy tính casio, tuy nhiên việc còn thiếu của chúng ta là miền giá trị của x.
Để tìm điều này ta xét \(y \leq 0;
\Rightarrow x^{2} + x - 12 \leq 0 \Leftrightarrow - 4 \leq x \leq
3\)
Sử dụng MODE 7 với thiết lập Start -4 End 3 Step \(\frac{7}{19}\)
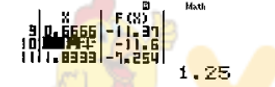
Quan sát bảng giá trị thu được ta thấy giá trị nhỏ nhất là: \(f(1,25) = - 11,6 \approx - 12\)
Vậy đáp án cần tìm là đáp án A.
Cách 2. Dùng phương pháp dồn biến đưa biểu thức P chứa hai biến thành biểu thức chứa 1 biến x.
\(\Leftrightarrow P = (x + 2)\left( x^{2}
+ x - 12 \right) + x + 17 = x^{3} + 3x^{2} - 9x - 7\)
Đặt \(f(x) = x^{3} + 3x^{2} - 9x -
7\)
Tìm miền giá trị của x ta có: \(y \leq 0;
\Rightarrow x^{2} + x - 12 \leq 0 \Leftrightarrow - 4 \leq x \leq
3\)
Khảo sát hàm số \(f(x) = x^{3} + 3x^{2} -
9x - 7\) ta có:
\(f'(x) = 3x^{2} + 6x - 9\)
\(f'(x) = 0 \Leftrightarrow
\left\lbrack \begin{matrix}
x = 1 \\
x = - 3
\end{matrix} \right.\)
So sánh \(\left\{ \begin{matrix}
f(1) = - 12;f( - 3) = 20 \\
f( - 4) = 13;f(3) = 20
\end{matrix} \right.\). Vậy giá trị nhỏ nhất cần tìm là -12 khi \(x = 1\)
Nhận xét: Một bài toán tìm giá trị nhỏ nhất sử dụng phương pháp dồn biến hay việc tìm cận và tìm giá trị nhỏ nhất có sự đóng góp rất lớn của Casio để tiết kiệm thời gian.
---------------------------------------------------------
Việc sử dụng máy tính CASIO để tìm GTLN, GTNN của hàm số là một kỹ năng quan trọng mà học sinh lớp 12 cần nắm vững khi bước vào giai đoạn luyện thi THPT Quốc gia. Không chỉ giúp kiểm tra nhanh kết quả, phương pháp này còn giúp bạn tối ưu thời gian làm bài trắc nghiệm. Tuy nhiên, để đạt hiệu quả cao nhất, bạn nên kết hợp giữa phương pháp giải tự luận và sử dụng máy tính cầm tay trong quá trình ôn luyện. Nếu bạn muốn tìm hiểu thêm các mẹo giải nhanh, bài tập luyện thi hoặc hướng dẫn sử dụng máy tính CASIO trong các dạng toán khác, hãy tiếp tục theo dõi chuyên mục "Tìm giá trị lớn nhất nhỏ nhất của hàm số" trên VnDoc.com nhé. Chúc bạn học tốt và đạt điểm tối đa trong kỳ thi sắp tới!
