40 bài toán tối ưu thực tế có lời giải chi tiết
Bài toán tối ưu thực tế có lời giải chi tiết
Trong kỳ thi THPT Quốc gia và các đề kiểm tra Toán 12, bài toán tối ưu thực tế luôn là một trong những dạng bài được đánh giá cao về tính vận dụng và khả năng phân loại học sinh. Những bài toán này không chỉ yêu cầu học sinh hiểu vững kiến thức hàm số mà còn cần khả năng tư duy logic và ứng dụng vào các tình huống thực tế. Trong bài viết này, chúng tôi đã tổng hợp 40 bài toán tối ưu thực tế có lời giải chi tiết, được chọn lọc kỹ lưỡng từ đề thi thật, đề thi thử và sách tham khảo uy tín – giúp bạn luyện tập hiệu quả và tự tin chinh phục điểm cao.
Phần I. Đề bài các bài toán tối ưu thục tế
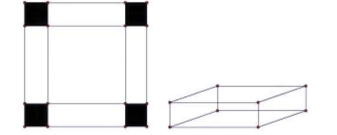
Câu 1: Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng ![]() \(x(cm)\), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm
\(x(cm)\), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm ![]() \(x\) để hộp nhận được có thể tích lớn nhất.
\(x\) để hộp nhận được có thể tích lớn nhất.
| A. |
B. |
C. |
D. |
Câu 2: Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ đó bằng ![]() \(1{dm}^{3}\) và diện tích toàn phần của hình trụ nhỏ nhất thì bán kính đáy của hình trụ phải bằng bao nhiêu?
\(1{dm}^{3}\) và diện tích toàn phần của hình trụ nhỏ nhất thì bán kính đáy của hình trụ phải bằng bao nhiêu?
| A. |
B. |
C. |
D. |
Câu 3: Khi nuôi cá thí nghiệm trong hồ, các nhà sinh học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ có cân nặng ![]() \(P = 960 -
20n\) (gam). Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
\(P = 960 -
20n\) (gam). Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
| A. 23 | B. 24 | C. 25 | D. 26 |
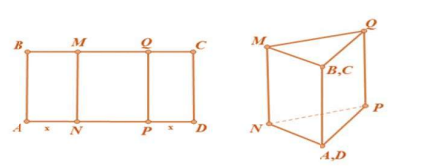
Câu 4: Cho một tấm nhôm hình chữ nhật ![]() \(ABCD\) có
\(ABCD\) có ![]() \(AD =60cm\) và
\(AD =60cm\) và ![]() \(AB\) có độ dài không đối. Ta gập tấm nhôm theo 2 cạnh MN và PQ vào phía trong đến khi
\(AB\) có độ dài không đối. Ta gập tấm nhôm theo 2 cạnh MN và PQ vào phía trong đến khi ![]() \(AB\) và
\(AB\) và ![]() \(DC\) trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết 2 đáy.
\(DC\) trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết 2 đáy.
| A. x = 20 | B. x = 25 | C. x = 10 | D. x = 30 |
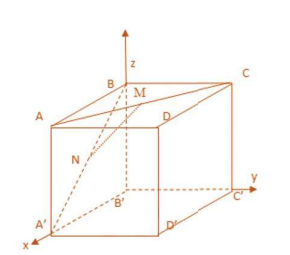
Câu 5: Bên trong một căn phòng hình lập phương, dược ký hiệu như sau  \(ABCD \cdot
A^{'}B^{'}C^{'}D^{'}\) cạnh bằng
\(ABCD \cdot
A^{'}B^{'}C^{'}D^{'}\) cạnh bằng ![]() \(4cm\). Người ta tiến hành trang trí ngôi nhà bằng cách gắn các dây lụa tại điểm
\(4cm\). Người ta tiến hành trang trí ngôi nhà bằng cách gắn các dây lụa tại điểm ![]() \(M\) và
\(M\) và ![]() \(N\) theo thứ tự trên
\(N\) theo thứ tự trên ![]() \(AC\) và
\(AC\) và  \(A^{'}B\) sao cho
\(A^{'}B\) sao cho ![]() \(AM = A^{'}N = t(0 \leq t \leq 4\sqrt{2})
(cm)\). Biết rằng dây lụa được nhập khẩu từ nước ngoài nên rất đắt. Gia chủ muốn chiều dài của dây là ngắn nhất. Hỏi độ dài ngắn nhất của sợi dây mà gia chủ có thể dùng là bao nhiêu?
\(AM = A^{'}N = t(0 \leq t \leq 4\sqrt{2})
(cm)\). Biết rằng dây lụa được nhập khẩu từ nước ngoài nên rất đắt. Gia chủ muốn chiều dài của dây là ngắn nhất. Hỏi độ dài ngắn nhất của sợi dây mà gia chủ có thể dùng là bao nhiêu?
| A. |
B. |
C. |
D. |
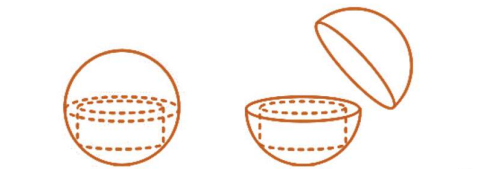
Câu 6: Công ty mỹ phẩm cho ra một mẫu sản phẩm dưỡng trắng da chống lão hóa mới mang tên Sakura với thiết kế là một khối cầu nhu một viên bi khổng lồ, bên trong là một khối trụ nằm phần nữa để đựng kem dưỡng da (như hỉnh vẽ). Theo dự kiến nhà sản xuất dự định để khối cầu có bán kính ![]() \(R = 2\sqrt{6}(cm)\). Tìm thể tích lớn nhất của khối trụ đựng kem để thể tích thực ghi trên bìa hộp là lớn nhất (nhằm thu hút khách hàng).
\(R = 2\sqrt{6}(cm)\). Tìm thể tích lớn nhất của khối trụ đựng kem để thể tích thực ghi trên bìa hộp là lớn nhất (nhằm thu hút khách hàng).
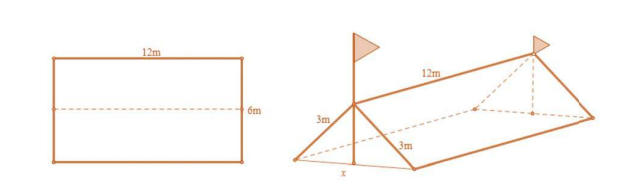
Câu 7: Trong đợt chào mùng ngày 26/03/2016, trường THPT Lê Quảng Chí có tổ chức cho học sinh các lớp tham quan dã ngoại ngoài trời, trong số đó có lớp 12A. Để có thể có chỗ nghi ngơi trong quá trình tham quan dã ngoại, lớp 12A đã dựng trên mặt đất bằng phẳng 1 chiếc lều bằng bạt từ một tấm bạt hình chữ nhật có chiều dài là 12 m và chiều rộng là 6 m bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm bạt sao cho hai mép chiều dài còn lại của tấm bạt sát đất và cách nhau ![]() \(x(m)\) (xem hình vẽ). Tìm
\(x(m)\) (xem hình vẽ). Tìm ![]() \(x\) để khoảng không gian phía trong lều là lớn nhất?
\(x\) để khoảng không gian phía trong lều là lớn nhất?
| A. |
B. |
C. |
D. |
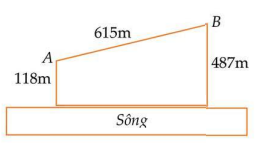
Câu 8. Cho hai vị trí A và B cách nhau 615m, cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách từ A và từ B đến bờ sông lần lượt là 118m và 487m. Một người đi từ A đến bờ sông để lấy nước mang về B. Đoạn đường ngắn nhất mà người đó có thể đi là:
| A. 569,5m | B. 671,4m | C. 779,8m | D. 741,2m |
Câu 9. Trong bài thực hành của môn huấn luyện quân sự có tình huống chiến sĩ phải bơi qua một con sông để tấn công một mục tiêu ở phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi của chiến sĩ bằng một nửa vận tốc chạy trên bộ. Hãy cho biết chiến sĩ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất, nếu như dòng sông là thẳng, mục tiêu ở cách chiến sĩ 1km theo đường chim bay và chiến sĩ cách bờ bên kia sông 100m.
| A. |
B. 100 | C. |
D. |
Câu 10. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có thể tích bằng ![]() \(\frac{500}{3}m^{3}\). Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500.000 đồng/m3. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất. Chi phí đó là?
\(\frac{500}{3}m^{3}\). Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500.000 đồng/m3. Hãy xác định kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất. Chi phí đó là?
| A. 74 triệu đồng | B. 75 triệu đồng | C. 76 triệu đồng | D. 77 triệu đồng |
Câu 11. Có hai chiếc cọc cao 10m và 30m lần lượt đặt tại hai vị trí A, B. Biết khoảng cách hai cọc là bằng 24m. Người ta chọn một cái chốt ở vị trí M trên mặt đất nằm giữa hai chân cột để giăng dây nối đến hai đỉnh C và D của cọc. Hỏi ta phải đặt chốt ở vị trí nào trên mặt đất để tổng độ dài của hai sợi dây đó là ngắn nhất:
A. AM = 6m, BM = 8m
B. AM = 7m, BM = 17m
C. AM = 4m, BM = 20m
D. AM = 12m, BM = 12m
Câu 12. Cho một hình lăng trụ đứng có đáy là tam giác đều. Thể tích của hình lăng trụ là V. Để diện tích toàn phần của hình lăng trụ nhỏ nhất thì cạnh đáy của hình lăng trụ là:
A. ![]() \(\sqrt[3]{4V}\) B.
\(\sqrt[3]{4V}\) B. ![]() \(\sqrt[3]{V}\) C.
\(\sqrt[3]{V}\) C. ![]() \(\sqrt[3]{2V}\) D.
\(\sqrt[3]{2V}\) D. ![]() \(\sqrt[3]{6V}\)
\(\sqrt[3]{6V}\)
Câu 13. Cần phải xây dựng một hố ga, dạng hình hộp chữ nhật có thể tích ![]() \(3\left( m^{3} \right)\). Tỉ số giữa chiều cao của hố (h) và chiều rộng của đáy (y) bằng 4. Biết rằng hố ga chỉ có các mặt bên và mặt đáy (không có mặt trên). Chiều dài của đáy (x) gần nhất với giá trị nào ở dưới để người thợ tốn ít nguyên vật liệu để xây hố ga?
\(3\left( m^{3} \right)\). Tỉ số giữa chiều cao của hố (h) và chiều rộng của đáy (y) bằng 4. Biết rằng hố ga chỉ có các mặt bên và mặt đáy (không có mặt trên). Chiều dài của đáy (x) gần nhất với giá trị nào ở dưới để người thợ tốn ít nguyên vật liệu để xây hố ga?
A. 1 B. 1,5 C. 2 D. 2,5
Câu 14: Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C. Khoảng cách ngắn nhất từ C đến B là 1km. Khoảng cách từ B đến A là 4km. Mỗi km dây điện đặt dưới nước là mất 5000USD, còn đặt dưới mặt đất mất 3000USD. Hỏi điểm S trên bờ cách A bao nhiêu để khi mắc dây điện từ A qua S rồi đến C là ít tốn kém nhất?
A. ![]() \(\frac{15}{4}(km)\) B.
\(\frac{15}{4}(km)\) B. ![]() \(\frac{13}{4}(km)\) C.
\(\frac{13}{4}(km)\) C. ![]() \(\frac{10}{4}(km)\) D.
\(\frac{10}{4}(km)\) D. ![]() \(\frac{19}{4}(km)\)
\(\frac{19}{4}(km)\)
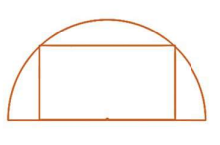
Câu 17: Một học sinh vẽ hình chữ nhật nội tiếp nửa đường tròn đường kính d, có một cạnh trùng vói đường kính hình tròn (như hình vẽ). Gọi x là độ dài cạnh hình chữ nhật không trùng với đường kính. Tính diện tích nửa hình tròn theo ![]() \(x\), biết diện tích hình chữ nhật đã cho là lớn nhất.
\(x\), biết diện tích hình chữ nhật đã cho là lớn nhất.
A. ![]() \(\frac{1}{4}\pi x^{2}\) B.
\(\frac{1}{4}\pi x^{2}\) B. ![]() \(\pi x^{2}\) C.
\(\pi x^{2}\) C. ![]() \(\frac{1}{2}\pi x^{2}\) D.
\(\frac{1}{2}\pi x^{2}\) D. ![]() \(2\pi x^{2}\)
\(2\pi x^{2}\)
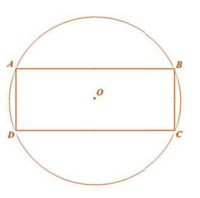
Câu 18: Một kĩ sư thiết kế sân tập thể thao dạng hình chữ nhật ABCD diện tích bằng ![]() \(961{\text{ }m}^{2}\) và được mở rộng thêm 4 phần đất sao cho tạo thành đường tròn ngoại tiếp hình chữ nhật ABCD có tâm
\(961{\text{ }m}^{2}\) và được mở rộng thêm 4 phần đất sao cho tạo thành đường tròn ngoại tiếp hình chữ nhật ABCD có tâm ![]() \(O\) là giao điểm hai đường chéo
\(O\) là giao điểm hai đường chéo ![]() \(AC\) và
\(AC\) và ![]() \(BD\). Tính diện tích nhỏ nhất (có thể đạt được) của 4 phần đất được mở rộng. (Xem hình vẽ bên)
\(BD\). Tính diện tích nhỏ nhất (có thể đạt được) của 4 phần đất được mở rộng. (Xem hình vẽ bên)
A. ![]() \(961\pi - 961{\text{
}m}^{2}\) C.
\(961\pi - 961{\text{
}m}^{2}\) C. ![]() \(1922\pi - 961{\text{
}m}^{2}\)
\(1922\pi - 961{\text{
}m}^{2}\)
B. ![]() \(1892\pi - 946{\text{
}m}^{2}\) D.
\(1892\pi - 946{\text{
}m}^{2}\) D. ![]() \(480,5\pi - 961{\text{
}m}^{2}\)
\(480,5\pi - 961{\text{
}m}^{2}\)
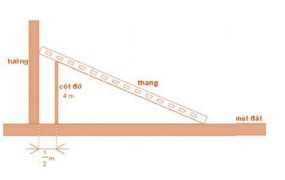
Câu 19: Tính chiều dài bé nhất của cái thang đơn vị m, để nó có thể tựa nào tường và mặt đất, ngang qua cột đỡ cao 4 m, song song và cách tường ![]() \(0,5\text{ }m\) kể từ tâm của cột đỡ (xem hình vẽ, kết quả lấy đến 2 chữ số thập phân).
\(0,5\text{ }m\) kể từ tâm của cột đỡ (xem hình vẽ, kết quả lấy đến 2 chữ số thập phân).
A. ![]() \(5,49\text{ }m\) C.
\(5,49\text{ }m\) C. ![]() \(5,59\text{ }m\) B.
\(5,59\text{ }m\) B. ![]() \(5,69\text{ }m\) D.
\(5,69\text{ }m\) D. ![]() \(5,79\text{ }m\)
\(5,79\text{ }m\)
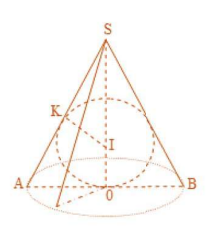
Câu 20: Một hạt ngọc trai hình cầu (S) bán kính ![]() \(R\) không đổi, được bọc trong một hộp trang sức dạng hình nón
\(R\) không đổi, được bọc trong một hộp trang sức dạng hình nón ![]() \((N)\) ngoại tiếp mặt cầu (S). Khi đó thì chiều cao h và bán kính đáy r của hình nón (N) lâ̂n lượt bằng bao nhiêu để hộp trang sức có thể tích nhỏ nhất?
\((N)\) ngoại tiếp mặt cầu (S). Khi đó thì chiều cao h và bán kính đáy r của hình nón (N) lâ̂n lượt bằng bao nhiêu để hộp trang sức có thể tích nhỏ nhất?
A. ![]() \(\left\{ \begin{matrix}
h = 4R \\
r = R\sqrt{2}
\end{matrix} \right.\) B.
\(\left\{ \begin{matrix}
h = 4R \\
r = R\sqrt{2}
\end{matrix} \right.\) B. ![]() \(\left\{ \begin{matrix}
h = 3R \\
r = R\sqrt{3}
\end{matrix} \right.\) C.
\(\left\{ \begin{matrix}
h = 3R \\
r = R\sqrt{3}
\end{matrix} \right.\) C. ![]() \(\left\{ \begin{matrix}
h = R\sqrt{2} \\
r = 4R
\end{matrix} \right.\) D.
\(\left\{ \begin{matrix}
h = R\sqrt{2} \\
r = 4R
\end{matrix} \right.\) D. ![]() \(\left\{ \begin{matrix}
h = R\sqrt{3} \\
r = 4R
\end{matrix} \right.\)
\(\left\{ \begin{matrix}
h = R\sqrt{3} \\
r = 4R
\end{matrix} \right.\)
Câu 21: Trong một cuộc thi, thử thách đặt ra là: BTC sẽ cấp cho bạn một chiếc xe máy, có một đoạn dốc được tạo nên từ một mặt phẳng có thể thay đối được độ nghiêng từ gốc. Một cảm biến quang học được đặt sẵn ở độ cao nhất định so với mặt đất sẽ hoạt động nếu xe máy của bạn đạt đến độ cao này. Biết rằng nếu chiếc xe máy này đi lên con dốc có độ nghiêng là ![]() \(30^{\circ}\) thì đạt vận tốc
\(30^{\circ}\) thì đạt vận tốc ![]() \(20\text{ }km/h\) và cứ nâng độ nghiêng thêm
\(20\text{ }km/h\) và cứ nâng độ nghiêng thêm ![]() \(4^{0}\) thì vận tốc xe máy giảm
\(4^{0}\) thì vận tốc xe máy giảm ![]() \(5\text{ }km/h\). Hỏi để đạt đến độ cao đề ra sớm nhất ta nên đặt mặt phẳng ban đầu có độ nghiêng là bao nhiêu?
\(5\text{ }km/h\). Hỏi để đạt đến độ cao đề ra sớm nhất ta nên đặt mặt phẳng ban đầu có độ nghiêng là bao nhiêu?
A. ![]() \(30^{0}\) B.
\(30^{0}\) B. ![]() \(45^{0}\) C.
\(45^{0}\) C. ![]() \(60^{\circ}\) D.
\(60^{\circ}\) D. ![]() \(90^{\circ}\)
\(90^{\circ}\)
Tài liệu vẫn còn, mời các bạn tải về
Phần II. Hướng dẫn giải chi tiết bài tập thực tế
Câu 1.
Gọi x (0 < x < 6) là độ dài cạnh hình vuông bị cắt
Thể tích khối hộp tạo thành bằng ![]() \(V =
x.(12 - 2x)^{2}\left( cm^{3} \right)\)
\(V =
x.(12 - 2x)^{2}\left( cm^{3} \right)\)
Áp dụng bất đẳng thức AM – GM (Cauchy) cho 3 số dương ta có:
![]() \(x.(12 - 2x)^{2} = 2.2x(6 - x)(6 -
x)\)
\(x.(12 - 2x)^{2} = 2.2x(6 - x)(6 -
x)\)![]() \(\leq 2\frac{(2x + 6 - x + 6 -
x)^{3}}{27} = 128\left( cm^{3} \right)\)
\(\leq 2\frac{(2x + 6 - x + 6 -
x)^{3}}{27} = 128\left( cm^{3} \right)\)
Dấu “=” xảy ra khi và chỉ khi ![]() \(2x = 6 - x
\Leftrightarrow x = 2\)
\(2x = 6 - x
\Leftrightarrow x = 2\)
Chọn đáp án C.
Câu 2.
Đặt bán kính đáy, chiều cao của lon sữa bò hình trụ lần lượt là r; h (đơn vị: dm)
Theo đề bài ra ta có:
![]() \(h\pi r^{2} = 1 \Rightarrow h =
\frac{1}{\pi r^{2}}(dm)\)
\(h\pi r^{2} = 1 \Rightarrow h =
\frac{1}{\pi r^{2}}(dm)\)
Diện tích toàn phần của hình trụ nhỏ nhất khi ![]() \(S = 2\pi r^{2} + 2\pi rh\) nhỏ nhất
\(S = 2\pi r^{2} + 2\pi rh\) nhỏ nhất
Ta có:
![]() \(S = 2\pi r^{2} + \frac{2}{r} = 2\pi
r^{2} + \frac{1}{r} + \frac{1}{r}\)
\(S = 2\pi r^{2} + \frac{2}{r} = 2\pi
r^{2} + \frac{1}{r} + \frac{1}{r}\)![]() \(\geq 3\sqrt[3]{2\pi
r^{2}.\frac{1}{r}.\frac{1}{r}} = 3\sqrt[3]{2\pi}\)
\(\geq 3\sqrt[3]{2\pi
r^{2}.\frac{1}{r}.\frac{1}{r}} = 3\sqrt[3]{2\pi}\)
Dấu “=” xảy ra khi ![]() \(2\pi r^{2} =
\frac{1}{r} \Leftrightarrow r =
\frac{1}{\sqrt[3]{2\pi}}(dm)\)
\(2\pi r^{2} =
\frac{1}{r} \Leftrightarrow r =
\frac{1}{\sqrt[3]{2\pi}}(dm)\)
Chọn đáp án B
Câu 3.
Cân nặng của cả bầy cá sau một vụ thu hoạch là:
![]() \(N = P.n = (960 - 20n).n\) (gam)
\(N = P.n = (960 - 20n).n\) (gam)
Để sau một vụ thu hoạch được nhiều cá nhất
Tường đương với việc ta cần tìm giá trị của n sao cho N đạt giá trị lớn nhất
Áp dụng bất đẳng thức AM – GM (Cauchy) cho hai số dương ta có:
![]() \(N = (960 - 20n).n = 20n(48 -
n)\)
\(N = (960 - 20n).n = 20n(48 -
n)\)![]() \(\leq 20.\frac{(n + 48 - n)^{2}}{4} =
11520(g)\)
\(\leq 20.\frac{(n + 48 - n)^{2}}{4} =
11520(g)\)
Dấu “=” xảy ra khi ![]() \(n = 48 - n
\Leftrightarrow n = 24\)
\(n = 48 - n
\Leftrightarrow n = 24\)
Chọn đáp án B
Tài liệu vẫn còn, mời các bạn tải về
--------------------------------------------------------
Qua 40 bài toán tối ưu thực tế có lời giải chi tiết được chia sẻ trong bài viết, hy vọng bạn đã nắm được cách tiếp cận và giải quyết hiệu quả dạng bài này. Đây không chỉ là tài liệu luyện thi hữu ích cho học sinh lớp 12 mà còn là nguồn tham khảo giá trị cho giáo viên, phụ huynh và những ai đang tìm kiếm những bài toán có tính ứng dụng cao trong đời sống. Hãy lưu lại bài viết và luyện tập thường xuyên để rèn kỹ năng phân tích, lập mô hình toán học và xử lý tình huống một cách logic. Đừng quên theo dõi [Tên website của bạn] để cập nhật thêm nhiều bài toán tối ưu thực tế có đáp án và các chuyên đề ôn thi Toán THPT Quốc gia khác. Chúc bạn học tập hiệu quả và đạt kết quả như mong đợi!









