Tìm điểm M thuộc mặt phẳng (P) để biểu thức MA - MB lớn nhất
Bài toán tìm điểm thuộc mặt phẳng để biểu thức MA - MB đạt max
Trong quá trình ôn thi THPT Quốc gia môn Toán, các bài toán hình học không gian, đặc biệt là những bài liên quan đến biểu thức khoảng cách như MA - MB đạt giá trị lớn nhất thường xuất hiện trong đề thi. Bài toán Tìm điểm M thuộc mặt phẳng (P) để biểu thức MA - MB lớn nhất là một ví dụ điển hình yêu cầu học sinh vận dụng kiến thức về hình học giải tích, mặt phẳng, vectơ và khoảng cách.
A. Cách tìm điểm M thuộc mặt phẳng (P) để biểu thức MA – MB đạt max
Phương pháp giải
Đối với hiệu ![]() : Chúng ta thường đánh giá
: Chúng ta thường đánh giá ![]() , dấu bằng có khi M, A, B thẳng hàng và M ngoài đoạn AB.
, dấu bằng có khi M, A, B thẳng hàng và M ngoài đoạn AB.
Đối với mặt phẳng thì chúng ta có khái niệm hai điểm “Cùng phía hoặc khác phía”, nhưng đối với đường thẳng thì sao?
Do đó ta có phương pháp tổng quát cho bài toán tìm ![]() với vị trí của điểm M cần tìm thuộc mp
với vị trí của điểm M cần tìm thuộc mp![]() hoặc đường thẳng
hoặc đường thẳng ![]() bất kể cùng phía hay khác phía.
bất kể cùng phía hay khác phía.
Gọi ![]() lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của ![]() trên
trên ![]() (hoặc
(hoặc ![]() ). Đặt
). Đặt ![]() và
và ![]() .
.
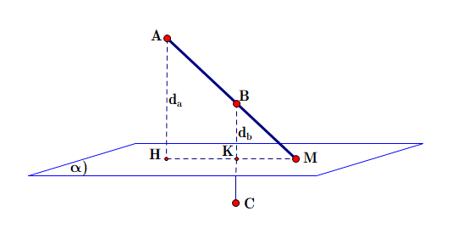
Đối với bài ![]() : Vị trí M ngoài đoạn
: Vị trí M ngoài đoạn ![]() và thỏa mãn hệ thức vectơ:
và thỏa mãn hệ thức vectơ:
![]()

B. Bài tập minh họa tìm M ∈ (P) để MA - MB lớn nhất
Ví dụ 1. Trong không gian ![]() , cho mặt phẳng
, cho mặt phẳng ![]() và hai điểm
và hai điểm ![]() ,
, ![]() . Điểm
. Điểm ![]() thuộc
thuộc ![]() và
và ![]() lớn nhất. Giá trị
lớn nhất. Giá trị ![]() bằng
bằng
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Ghi ![]() CALC nhập tọa độ A, kết quả
CALC nhập tọa độ A, kết quả ![]() . CALC nhập tọa độ B, kết quả
. CALC nhập tọa độ B, kết quả ![]() .
.
Ta có tỉ số ![]() . Tìm hình chiếu H, K của A, B trên (P).
. Tìm hình chiếu H, K của A, B trên (P).
Ghi ![]() bấm = STO B, Bấm 🞁 CALC nhập tọa độ A STO A.
bấm = STO B, Bấm 🞁 CALC nhập tọa độ A STO A.
Tọa độ M thỏa mãn  .
.
Đến đây ta ghi: ![]() bấm = thì
bấm = thì ![]() , sửa thành
, sửa thành ![]() bấm = thì
bấm = thì ![]() , sửa thành
, sửa thành ![]() bấm = thì
bấm = thì ![]() .
.
Vậy ![]() . Chọn C.
. Chọn C.
Ví dụ 2. Trong không gian ![]() , cho đường thẳng
, cho đường thẳng ![]() và hai điểm
và hai điểm ![]() ,
, ![]() . Điểm
. Điểm ![]() thuộc đường thẳng
thuộc đường thẳng ![]() sao cho
sao cho ![]() lớn nhất. Tính giá trị của biểu thức
lớn nhất. Tính giá trị của biểu thức ![]() .
.
A.![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Ghi ![]() CALC nhập
CALC nhập ![]() ta có
ta có ![]() . CALC nhập
. CALC nhập ![]() có
có ![]() nên tỉ số
nên tỉ số  .
.
Sửa lại là ![]() bấm = STO B, bấm 🞁 bấm CALC nhập lại
bấm = STO B, bấm 🞁 bấm CALC nhập lại ![]() STO A.
STO A.
Điểm M thuộc ![]() thỏa mãn
thỏa mãn ![]()
 .
.
Đến đây ghi: ![]() bấm = thì
bấm = thì ![]() , sửa thành
, sửa thành ![]() bấm = thì
bấm = thì ![]() , sửa thành
, sửa thành ![]() bấm = thì
bấm = thì ![]() .
.
Do đó tọa độ ![]() .
.
Vậy ![]() . Chọn B.
. Chọn B.
Ví dụ 3: Trong không gian ![]() , cho hai điểm
, cho hai điểm ![]() và
và ![]() Xét hai điểm
Xét hai điểm ![]() và
và ![]() thay đổi thuộc mặt phẳng
thay đổi thuộc mặt phẳng ![]() sao cho
sao cho ![]() . Giá trị lớn nhất của
. Giá trị lớn nhất của ![]() bằng:
bằng:
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Cách 1: Vẽ yếu tố phụ.

Vì A, B khác phía đối với mp ![]() nên lấy
nên lấy  đối xứng với
đối xứng với ![]() qua
qua ![]() .
.
Vẽ ![]() , khi đó
, khi đó ![]() .
.
Dấu bằng xảy ra khi và chỉ khi A’, C, M thẳng hàng.
Gọi ![]() là hình chiếu của A, B trên mp
là hình chiếu của A, B trên mp![]() , độ dài
, độ dài ![]() .
.
Suy ra  . Chọn D.
. Chọn D.
Cách 2. Tổng quát – Khảo sát hàm số.

Gọi ![]() là hình chiếu của A, B trên mp
là hình chiếu của A, B trên mp![]() , độ dài
, độ dài ![]() .
.
Ta chọn M, N ngoài đoạn HK (Điểm M càng xa điểm A càng tốt, điểm N càng gần B càng tốt; Kể cả A và B cùng phía hay khác phía đối với ![]() , chúng ta cần quan tâm ở đây là
, chúng ta cần quan tâm ở đây là ![]() ). Đặt
). Đặt ![]() , ta xét hàm số:
, ta xét hàm số:
![]()

 . Suy ra
. Suy ra ![]() . Chọn D.
. Chọn D.
Cách 3. Tổng quát – Bất đẳng thức.
Khi thiết lập được hàm số, thì dùng BĐT Mincopxki ta có:
![]()
![]()
Đẳng thức có khi ![]()
Nhận xét:
Khi ![]() lớn nhất thì ta có các tam giác
lớn nhất thì ta có các tam giác ![]() đồng dạng, tỉ số bằng 2.
đồng dạng, tỉ số bằng 2.
Khi đó: ![]() , nên
, nên ![]() .
.
Như vậy ta vẫn có tỉ số ![]() . Vậy đây xem như một cách giải (Thừa nhận kết quả).
. Vậy đây xem như một cách giải (Thừa nhận kết quả).
Các bài toán trên có đặc điểm: ![]() . Hay ta có
. Hay ta có ![]() , nói cách khác, các đường thẳng
, nói cách khác, các đường thẳng ![]() cùng tạo với
cùng tạo với ![]() một góc bằng nhau
một góc bằng nhau ![]() . Mà ta có
. Mà ta có ![]() . Ta tạm gọi là “Định luật phản xạ ánh sáng đối với gương phẳng!”: Tia phản xạ của AM sẽ theo phương BN; Tia phản xạ của BN sẽ theo phương AM.
. Ta tạm gọi là “Định luật phản xạ ánh sáng đối với gương phẳng!”: Tia phản xạ của AM sẽ theo phương BN; Tia phản xạ của BN sẽ theo phương AM.
Trong trường hợp khi ![]()
![]() , có nghĩa là một điểm M di động trên
, có nghĩa là một điểm M di động trên ![]() , ta quy về bài toán “Tìm M thuộc
, ta quy về bài toán “Tìm M thuộc ![]() hoặc
hoặc ![]() để
để ![]() lớn nhất”. Khi đó ta giải quyết bài toán theo cách tổng quát như trên (Có thể dùng CASIO để tìm max). Tia AM, BM hoặc trùng nhau hoặc đối xứng nhau qua mặt phẳng
lớn nhất”. Khi đó ta giải quyết bài toán theo cách tổng quát như trên (Có thể dùng CASIO để tìm max). Tia AM, BM hoặc trùng nhau hoặc đối xứng nhau qua mặt phẳng ![]() hoặc mặt phẳng pháp tuyến của
hoặc mặt phẳng pháp tuyến của ![]() tại M; Kể cả bài toán
tại M; Kể cả bài toán ![]() .
.
C. Bài tập tự rèn luyện tìm M thuộc (P) để MA – MB đạt max
Bài tập 1. Trong không gian với hệ tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() ,
, ![]() . Lấy điểm
. Lấy điểm ![]() thuộc mặt phẳng
thuộc mặt phẳng ![]() sao cho
sao cho ![]() lớn nhất. Tọa độ
lớn nhất. Tọa độ ![]() là:
là:
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Bài tập 2. Trong không gian ![]() , cho đường thẳng
, cho đường thẳng ![]() và hai điểm
và hai điểm![]() ,
, ![]() . Biết điểm
. Biết điểm ![]() thuộc
thuộc ![]() sao cho biểu thức
sao cho biểu thức ![]() đạt giá trị lớn nhất
đạt giá trị lớn nhất ![]() . Khi đó
. Khi đó ![]() bằng bao nhiêu?
bằng bao nhiêu?
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Bài tập 3. Trong không gian ![]() , cho 3 điểm
, cho 3 điểm ![]() ,
,![]() và
và ![]() . Điểm
. Điểm ![]() di động trong không gian sao cho
di động trong không gian sao cho ![]() . Biết
. Biết ![]() đạt giá trị lớn nhất tại điểm
đạt giá trị lớn nhất tại điểm ![]() . Tính tích số
. Tính tích số ![]() .
.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Bài tập 4. Trong không gian, cho hai điểm ![]() và
và ![]() . Xét hai điểm
. Xét hai điểm ![]() và
và ![]() thay đổi thuộc mặt phẳng (Oxy) sao cho
thay đổi thuộc mặt phẳng (Oxy) sao cho ![]() . Giá trị lớn nhất của
. Giá trị lớn nhất của ![]() bằng
bằng
A. ![]() B.
B. ![]() . C.
. C. ![]() D.
D. ![]() .
.
Đáp án bài tập tự rèn luyện
Bài tập 1.
Ta có tỉ số ![]() nên gọi C là điểm thỏa mãn
nên gọi C là điểm thỏa mãn ![]() . Khi đó điểm M cần tìm là hình chiếu của C trên
. Khi đó điểm M cần tìm là hình chiếu của C trên ![]() nên tọa độ
nên tọa độ ![]() . Chọn B.
. Chọn B.
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
--------------------------------------------------------------
Qua bài toán Tìm điểm M thuộc mặt phẳng (P) để biểu thức MA - MB lớn nhất, chắc chắn bạn đã nắm được cách tiếp cận một dạng toán quen thuộc nhưng đầy thử thách trong phần hình học không gian. Việc luyện tập những bài toán có độ phân hóa như thế này sẽ giúp bạn củng cố kỹ năng phân tích, áp dụng các công thức hình học giải tích, đồng thời chuẩn bị tâm lý vững vàng hơn cho kỳ thi THPT Quốc gia môn Toán sắp tới.










