VnDoc.com

Giá trị lượng giác của một góc bất kì từ 0o đến 180o

Chuyên đề môn Toán 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Chuyên đề

Phân loại: Tài liệu Tính phí

Chuyên đề Toán học lớp 10: Giá trị lượng giác của một góc bất kì từ 0^o đến 180^o được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo.

Bài: Giá trị lượng giác của một góc bất kì từ 0^o đến 180^o

1. Định nghĩa

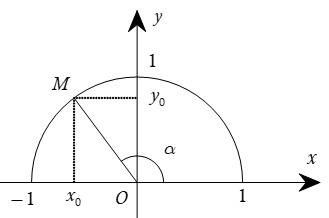
Trong mặt phẳng tọa độ $Oxy$, nửa đường tròn tâm $O$ nằm phía trên trục hoành có bán kính $R=1$ được gọi là nửa đường tròn đơn vị.

Với mỗi góc $\alpha$ $\alpha$ ( $0^{\circ} \le \alpha \le 180^{\circ}$ $0^{\circ} \le \alpha \le 180^{\circ}$) ta xác định một điểm $M$ trên nửa đường tròn đơn vị sao cho $\widehat {xOM} = \alpha$ $\widehat {xOM} = \alpha$ và điểm $M$ có tọa độ $M(x_0;y_0)$. Khi đó:

$\sin$ $\sin$ của góc $\alpha$ $\alpha$ là $y_0$, kí hiệu $\sin \alpha = {y_0}$ $\sin \alpha = {y_0}$.
côsin của góc $\alpha$ $\alpha$ là $x_0$, kí hiệu $\cos \alpha =x_0$ $\cos \alpha =x_0$.
tang của góc $\alpha$ $\alpha$ là $\frac{y_0}{x_0}$ $\frac{y_0}{x_0}$ ( $x_0 \neq 0$ $x_0 \neq 0$), kí hiệu $\tan \alpha = \frac{y_0}{x_0}$ $\tan \alpha = \frac{y_0}{x_0}$.
côtang của góc $\alpha$ $\alpha$ là $\frac {x_0}{y_0}$ $\frac {x_0}{y_0}$ ( $y_0 \neq 0$ $y_0 \neq 0$), kí hiệu $\cot \alpha = \frac {x_0}{y_0}$ $\cot \alpha = \frac {x_0}{y_0}$.

Các số $\sin \alpha ; \cos \alpha; \tan \alpha ; \cot \alpha$ $\sin \alpha ; \cos \alpha; \tan \alpha ; \cot \alpha$ là các giá trị lượng giác của góc $\alpha$ $\alpha$.

Hình vẽ minh họa:

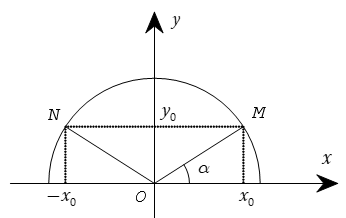
chuyên đề toán 10

2. Tính chất

Trên hình bên ta có dây cung NM song song với trục Ox và nếu ∠ xOM = α thì ∠xON = 180^o – α. Ta có yM = yN = y^o, xM = –xN = x^o. Do đó

sin α = sin(180^o – α)
cos α = –cos(180^o – α)
tan α = –tan(180^o – α)
cot α = –cot(180^o – α)

Hình vẽ minh họa

chuyên đề toán 10

Ví dụ: Đơn giản hóa các biểu thức sau:

a) $\sin 110^{\circ} +\cos 50^{\circ} -\sin70^{\circ} +\cos130^{\circ}$ $\sin 110^{\circ} +\cos 50^{\circ} -\sin70^{\circ} +\cos130^{\circ}$;

b) $-2\sin (180^{\circ} -\beta).\cot \beta + 3\cos \beta +\cos(180^{\circ} -\beta)$ $-2\sin (180^{\circ} -\beta).\cot \beta + 3\cos \beta +\cos(180^{\circ} -\beta)$.

Hướng dẫn giải

a) $\sin 110^{\circ} +\cos 50^{\circ} -\sin70^{\circ} +\cos130^{\circ}$ $\sin 110^{\circ} +\cos 50^{\circ} -\sin70^{\circ} +\cos130^{\circ}$

$= (\sin 110^{\circ} -\sin70^{\circ}) +(\cos130^{\circ}+\cos 50^{\circ})$ $= (\sin 110^{\circ} -\sin70^{\circ}) +(\cos130^{\circ}+\cos 50^{\circ})$

$= (\sin (180^\circ - 110^{\circ}) -\sin70^{\circ})$ $= (\sin (180^\circ - 110^{\circ}) -\sin70^{\circ})$ $+(\cos130^{\circ}-\cos (180^{\circ} -50^{\circ}))$ $+(\cos130^{\circ}-\cos (180^{\circ} -50^{\circ}))$

$=(\sin 70^{\circ} -\sin 70^{\circ} )+(\cos 130^{\circ} -\cos 130^{\circ} )=0$ $=(\sin 70^{\circ} -\sin 70^{\circ} )+(\cos 130^{\circ} -\cos 130^{\circ} )=0$.

b) $-2\sin (180^{\circ} -\beta).\cot \beta + 3\cos \beta +\cos(180^{\circ} -\beta)$ $-2\sin (180^{\circ} -\beta).\cot \beta + 3\cos \beta +\cos(180^{\circ} -\beta)$=

$-2\sin \beta.\cot \beta + 3\cos \beta -\cos\beta$ $-2\sin \beta.\cot \beta + 3\cos \beta -\cos\beta$ $-2\sin \beta. \frac {\cos\beta} {\sin \beta} + 3\cos \beta -\cos\beta =$ $-2\sin \beta. \frac {\cos\beta} {\sin \beta} + 3\cos \beta -\cos\beta =$

$-2\cos\beta + 3\cos \beta -\cos\beta=0$ $-2\cos\beta + 3\cos \beta -\cos\beta=0$.

3. Giá trị lượng giác của các góc đặc biệt

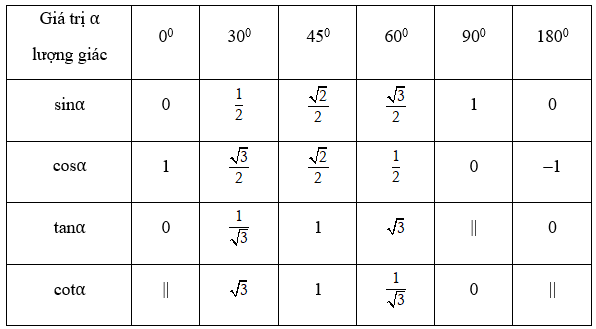
chuyên đề toán 10

Trong bảng kí hiệu “||” để chỉ giá trị lượng giác không xác định.

Chú ý. Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể suy ra giá trị lượng giác của một số góc đặc biệt khác.

Chẳng hạn:

sin 120^o = sin(180^o – 60^o) = sin60^o =
cos 135^o = cos(180^o – 45^o) = –cos45^o = -

4. Góc giữa hai vectơ

a) Định nghĩa

Cho hai vectơ đều khác vectơ 0 .Từ một điểm O bất kì ta vẽ Góc ∠AOB với số đo từ 0^o đến 180^o được gọi là góc giữa hai vectơ . Ta kí hiệu góc giữa hai vectơ là

Nếu = 90^o thì ta nói rằng vuông góc với nhau, kí hiệu là

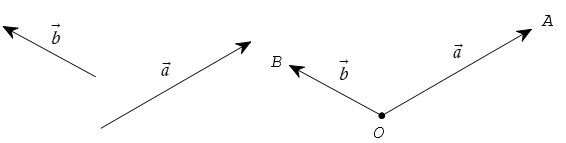
chuyên đề toán 10

b) Chú ý. Từ định nghĩa ta có .

Ví dụ: Điểm cuối của góc lượng giác $\alpha$ $\alpha$ ở góc phần tư thứ mấy nếu $\sin\alpha,\ cos\alpha$ $\sin\alpha,\ cos\alpha$ cùng dấu?

A. Thứ $II.$ B. Thứ $IV.$

C. Thứ $II$ hoặc $IV.$ D. Thứ $I$ hoặc $III.$

Hướng dẫn giải:

Điểm cuối của $\alpha$ $\alpha$ thuộc góc phần tư thứ nhất thì $\sin\alpha > 0$ $\sin\alpha > 0$, $\cos\alpha > 0$ $\cos\alpha > 0$.

Điểm cuối của $\alpha$ $\alpha$ thuộc góc phần tư thứ nhất thì $\sin\alpha < 0$ $\sin\alpha < 0$, $\cos\alpha < 0$ $\cos\alpha < 0$.

Vậy nếu $\sin\alpha,\ cos\alpha$ $\sin\alpha,\ cos\alpha$ cùng dấu thì điểm cuối của góc lượng giác $\alpha$ $\alpha$ ở góc phần tư thứ $I$ hoặc $III.$

Ví dụ: Cho $\pi < \alpha < \frac{3\pi}{2}$ $\pi < \alpha < \frac{3\pi}{2}$. Xác định dấu của biểu thức $M = \sin\left( \frac{\pi}{2} - \alpha ight).cot(\pi + \alpha).$ $M = \sin\left( \frac{\pi}{2} - \alpha ight).cot(\pi + \alpha).$

A. $M \geq 0.$ $M \geq 0.$ B. $M > 0.$ C. $M \leq 0.$ $M \leq 0.$ D. $M < 0.$

Hướng dẫn giải:

Ta có:

$\left\{ \begin{matrix} \pi < \alpha < \dfrac{3\pi}{2} \Rightarrow - \dfrac{3\pi}{2} < - \alpha < - \pi \\ \pi < \alpha < \dfrac{3\pi}{2} \Rightarrow 2\pi < \pi + \alpha < \dfrac{5\pi}{2} \\ \end{matrix} \right.$ $\left\{ \begin{matrix} \pi < \alpha < \dfrac{3\pi}{2} \Rightarrow - \dfrac{3\pi}{2} < - \alpha < - \pi \\ \pi < \alpha < \dfrac{3\pi}{2} \Rightarrow 2\pi < \pi + \alpha < \dfrac{5\pi}{2} \\ \end{matrix} \right.$

$ightarrow - \pi < \frac{\pi}{2} - \alpha < - \frac{\pi}{2}$ $ightarrow - \pi < \frac{\pi}{2} - \alpha < - \frac{\pi}{2}$ và $\overset{}{ightarrow}\cot(\pi + \alpha) > 0$ $\overset{}{ightarrow}\cot(\pi + \alpha) > 0$

$\overset{}{ightarrow}\sin\left( \frac{\pi}{2} - \alpha ight) < 0$ $\overset{}{ightarrow}\sin\left( \frac{\pi}{2} - \alpha ight) < 0$

$\overset{}{ightarrow}M < 0$ $\overset{}{ightarrow}M < 0$.

Ví dụ: Cho góc $\alpha$ $\alpha$ thỏa mãn $\tan\alpha = 2$ $\tan\alpha = 2$ và $180^{o} < \alpha < 270^{o}.$ $180^{o} < \alpha < 270^{o}.$ Tính $P = \cos\alpha + \sin\alpha.$ $P = \cos\alpha + \sin\alpha.$

A. $P = - \frac{3\sqrt{5}}{5}.$ $P = - \frac{3\sqrt{5}}{5}.$ B. $P = 1 - \sqrt{5}.$ $P = 1 - \sqrt{5}.$

C. $P = \frac{3\sqrt{5}}{2}.$ $P = \frac{3\sqrt{5}}{2}.$ D. $P = \frac{\sqrt{5} - 1}{2}.$ $P = \frac{\sqrt{5} - 1}{2}.$

Hướng dẫn giải:

Ta có $\left\{ \begin{matrix} cos^{2}\alpha = \dfrac{1}{1 + \tan^{2}\alpha} = \dfrac{1}{5} \Rightarrow \cos\alpha = \pm \dfrac{1}{\sqrt{5}} \\ 180^{o} < \alpha < 270^{o} \\ \end{matrix} \right.$ $\left\{ \begin{matrix} cos^{2}\alpha = \dfrac{1}{1 + \tan^{2}\alpha} = \dfrac{1}{5} \Rightarrow \cos\alpha = \pm \dfrac{1}{\sqrt{5}} \\ 180^{o} < \alpha < 270^{o} \\ \end{matrix} \right.$

$\overset{}{ightarrow}\cos\alpha = - \frac{1}{\sqrt{5}}$ $\overset{}{ightarrow}\cos\alpha = - \frac{1}{\sqrt{5}}$

$\overset{}{ightarrow}\sin\alpha = \tan\alpha.cos\alpha = - \frac{2}{\sqrt{5}}$ $\overset{}{ightarrow}\sin\alpha = \tan\alpha.cos\alpha = - \frac{2}{\sqrt{5}}$.

Do đó, $\sin\alpha + \cos\alpha = - \frac{3}{\sqrt{5}} = - \frac{3\sqrt{5}}{5}.$ $\sin\alpha + \cos\alpha = - \frac{3}{\sqrt{5}} = - \frac{3\sqrt{5}}{5}.$

Ví dụ: Cho góc $\alpha$ $\alpha$ thỏa mãn $\sin(\pi + \alpha) = - \frac{1}{3}$ $\sin(\pi + \alpha) = - \frac{1}{3}$ và $\frac{\pi}{2} < \alpha < \pi$ $\frac{\pi}{2} < \alpha < \pi$. Tính $P = \tan\left( \frac{7\pi}{2} - \alpha ight)$ $P = \tan\left( \frac{7\pi}{2} - \alpha ight)$.

A. $P = 2\sqrt{2}.$ $P = 2\sqrt{2}.$ B. $P = - 2\sqrt{2}.$ $P = - 2\sqrt{2}.$ C. $P = \frac{\sqrt{2}}{4}.$ $P = \frac{\sqrt{2}}{4}.$ D. $P = - \frac{\sqrt{2}}{4}.$ $P = - \frac{\sqrt{2}}{4}.$

Hướng dẫn giải

Ta có

$P = \tan\left( \frac{7\pi}{2} - \alpha ight) = \tan\left( 3\pi + \frac{\pi}{2} - \alpha ight)$ $P = \tan\left( \frac{7\pi}{2} - \alpha ight) = \tan\left( 3\pi + \frac{\pi}{2} - \alpha ight)$

$= \tan\left( \frac{\pi}{2} - \alpha ight) = \cot\alpha = \frac{\cos\alpha}{\sin\alpha}$ $= \tan\left( \frac{\pi}{2} - \alpha ight) = \cot\alpha = \frac{\cos\alpha}{\sin\alpha}$ .

Theo giả thiết ta có: $\sin(\pi + \alpha) = - \frac{1}{3}$ $\sin(\pi + \alpha) = - \frac{1}{3}$

$\Leftrightarrow - \sin\alpha = - \frac{1}{3} \Leftrightarrow \sin\alpha = \frac{1}{3}$ $\Leftrightarrow - \sin\alpha = - \frac{1}{3} \Leftrightarrow \sin\alpha = \frac{1}{3}$ .

Ta có $\left\{ \begin{matrix} \cos\alpha = \pm \sqrt{1 - sin^{2}\alpha} = \pm \dfrac{2\sqrt{2}}{3} \\ \dfrac{\pi}{2} < \alpha < \pi \\ \end{matrix} \right.$ $\left\{ \begin{matrix} \cos\alpha = \pm \sqrt{1 - sin^{2}\alpha} = \pm \dfrac{2\sqrt{2}}{3} \\ \dfrac{\pi}{2} < \alpha < \pi \\ \end{matrix} \right.$

$\overset{}{ightarrow}\cos\alpha = - \frac{2\sqrt{2}}{3}\overset{}{ightarrow}P = - 2\sqrt{2}.$ $\overset{}{ightarrow}\cos\alpha = - \frac{2\sqrt{2}}{3}\overset{}{ightarrow}P = - 2\sqrt{2}.$

Ví dụ: Cho góc $\alpha$ $\alpha$ thỏa mãn $\sin\alpha\cos\alpha = \frac{12}{25}$ $\sin\alpha\cos\alpha = \frac{12}{25}$ và $\sin\alpha + \cos\alpha > 0.$ $\sin\alpha + \cos\alpha > 0.$ Tính $P = sin^{3}\alpha + cos^{3}\alpha.$ $P = sin^{3}\alpha + cos^{3}\alpha.$

A. $P = \frac{91}{125} \cdot$ $P = \frac{91}{125} \cdot$ B. $P = \frac{49}{25} \cdot$ $P = \frac{49}{25} \cdot$ C. $P = \frac{7}{5} \cdot$ $P = \frac{7}{5} \cdot$ D. $P = \frac{1}{9} \cdot$ $P = \frac{1}{9} \cdot$

Hướng dẫn giải

Áp dụng hằng đẳng thức: $a^{3} + b^{3} = (a + b)^{3} - 3ab(a + b)$ $a^{3} + b^{3} = (a + b)^{3} - 3ab(a + b)$ , ta có:

$P = \sin^{3}\alpha +\cos^{3}\alpha$ $P = \sin^{3}\alpha +\cos^{3}\alpha$ $= \left( \sin\alpha +\cos\alpha \right)^{3} - 3\sin\alpha\cos\alpha\left( \sin\alpha + \cos\alpha \right).$ $= \left( \sin\alpha +\cos\alpha \right)^{3} - 3\sin\alpha\cos\alpha\left( \sin\alpha + \cos\alpha \right).$

Ta có $\left( \sin\alpha + \cos\alpha \right)^{2} = sin^{2}\alpha + 2sin\alpha\cos\alpha + \cos^{2}\alpha$ $\left( \sin\alpha + \cos\alpha \right)^{2} = sin^{2}\alpha + 2sin\alpha\cos\alpha + \cos^{2}\alpha$ $= 1 + \frac{24}{25} = \frac{49}{25}$ $= 1 + \frac{24}{25} = \frac{49}{25}$

Vì $\sin\alpha + \cos\alpha > 0$ $\sin\alpha + \cos\alpha > 0$ nên ta chọn $\sin\alpha + \cos\alpha = \frac{7}{5}$ $\sin\alpha + \cos\alpha = \frac{7}{5}$ .

Thay $\left\{ \begin{matrix} \sin\alpha + \cos\alpha = \dfrac{7}{5} \\ \sin\alpha\cos\alpha = \dfrac{12}{25} \\ \end{matrix} \right.$ $\left\{ \begin{matrix} \sin\alpha + \cos\alpha = \dfrac{7}{5} \\ \sin\alpha\cos\alpha = \dfrac{12}{25} \\ \end{matrix} \right.$ vào $P$ , ta được $P = \left( \frac{7}{5} ight)^{3} - 3.\frac{12}{25}.\frac{7}{5} = \frac{91}{125}$ $P = \left( \frac{7}{5} ight)^{3} - 3.\frac{12}{25}.\frac{7}{5} = \frac{91}{125}$ .

-----------------------------------------------------------

Với nội dung bài Giá trị lượng giác của một góc bất kì từ 0^o đến 180^o chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững định nghĩa tính chất của giá trị lượng giác của một góc.....

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Giá trị lượng giác của một góc bất kì từ 0^o đến 180^o. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Bơ

1

817

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!