VnDoc.com

Viết phương trình đường thẳng đi qua 2 điểm

Phương trình đường thẳng đi qua 2 điểm

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Phương trình đường thẳng

1. Phương trình tổng quát của đường thẳng
2. Phương trình tham số của đường thẳng
3. Cách viết phương trình đường thẳng đi qua hai điểm
4. Bài tập viết phương trình đường thẳng
5. Bài tập rèn luyện viết phương trình đường thẳng

Bạn đang tìm cách viết phương trình đường thẳng đi qua 2 điểm một cách nhanh chóng và chính xác? Trong hình học giải tích, việc xác định phương trình đường thẳng từ hai điểm đã biết tọa độ là kỹ năng cơ bản nhưng vô cùng quan trọng, giúp bạn giải quyết hiệu quả nhiều dạng bài tập từ cơ bản đến nâng cao.
Trong bài viết này, chúng ta sẽ cùng nhau khám phá chi tiết công thức tổng quát, ví dụ minh họa dễ hiểu và những mẹo áp dụng nhanh phương trình đường thẳng đi qua 2 điểm, giúp bạn học tốt hơn và tiết kiệm thời gian ôn luyện.

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

1. Phương trình tổng quát của đường thẳng

Đường thẳng Δ có phương trình tổng quát là: $ax + by + c = 0;\left( {{a^2} + {b^2} \ne 0} \right)$ $ax + by + c = 0;\left( {{a^2} + {b^2} \ne 0} \right)$ nhận $\overrightarrow n = \left( {a;b} \right)$ $\overrightarrow n = \left( {a;b} \right)$ làm vectơ pháp tuyến.

2. Phương trình tham số của đường thẳng

- Phương trình tham số của đường thẳng đi qua điểm $A\left( {{x_0},{y_0}} \right)$ $A\left( {{x_0},{y_0}} \right)$ nhận $\overrightarrow u (a,b)$ $\overrightarrow u (a,b)$ làm vecto chỉ phương, Ta có:

$B\left( {x,y} \right) \in d \Leftrightarrow \overrightarrow {AB} = t\overrightarrow u \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x - {x_0} = at} \\ {y - {y_0} = bt} \end{array}} \right.$ $B\left( {x,y} \right) \in d \Leftrightarrow \overrightarrow {AB} = t\overrightarrow u \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x - {x_0} = at} \\ {y - {y_0} = bt} \end{array}} \right.$

$\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x = {x_0} + at} \\ {y = {y_0} + bt} \end{array}} \right.;\left( {{a^2} + {b^2} \ne 0,t \in \mathbb{R}} \right)$ $\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x = {x_0} + at} \\ {y = {y_0} + bt} \end{array}} \right.;\left( {{a^2} + {b^2} \ne 0,t \in \mathbb{R}} \right)$

- Đường thẳng d đi qua điểm $A\left( {{x_0},{y_0}} \right)$ $A\left( {{x_0},{y_0}} \right)$, nhận $\overrightarrow u (a,b)$ $\overrightarrow u (a,b)$ là vecto chỉ phương, phương trình chính tắc của đường thẳng là $\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}$ $\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b}$ với $(a,b \ne 0)$ $(a,b \ne 0)$

3. Cách viết phương trình đường thẳng đi qua hai điểm

a. Sử dụng định nghĩa

Bài toán: Cho hai điểm A(a, b), B(c, d). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B.

Phương pháp:

Bước 1: Tính: $\overrightarrow {AB} = \left( {c - a;d - b} \right)$ $\overrightarrow {AB} = \left( {c - a;d - b} \right)$ (vectơ chỉ phương của đường thẳng d)

Bước 2: Xác định vectơ pháp tuyến của đường thẳng d: $\overrightarrow n = \left( {b - d;c - a} \right)$ $\overrightarrow n = \left( {b - d;c - a} \right)$

Bước 3: Phương trình đường thẳng d:

$\left( {b - d} \right)\left( {x - a} \right) + \left( {c - a} \right)\left( {y - b} \right) = 0$ $\left( {b - d} \right)\left( {x - a} \right) + \left( {c - a} \right)\left( {y - b} \right) = 0$

b. Sử dụng phương trình tổng quát

Bài toán: Cho hai điểm A(a, b), B(c, d). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B.

Phương pháp:

Bước 1: Gọi phương trình tổng quát của đường thẳng d là y = mx + n (*)

Bước 2: Thay tọa độ A, B vào phương trình tổng quát ta thu được hệ phương trình ẩn m, n

$\left\{ {\begin{array}{*{20}{c}} {b = am + n} \\ {d = cm + n} \end{array}} \right. \Rightarrow \left( {m;n} \right) = \left( {?;?} \right)$ $\left\{ {\begin{array}{*{20}{c}} {b = am + n} \\ {d = cm + n} \end{array}} \right. \Rightarrow \left( {m;n} \right) = \left( {?;?} \right)$

Thay m, n vừa tìm được vào phương trình (*) ta suy ra phương trình cần tìm.

4. Bài tập viết phương trình đường thẳng

Ví dụ 1: Viết phương trình đường thẳng tham số, phương trình tổng quát đi qua 2 điểm A (1;2) và B (2;3). Vẽ đường thẳng vừa tìm được trên hệ tọa độ Oxy.

Hướng dẫn giải

Cách 1: Sử dụng định nghĩa

Cách 2: Sử dụng phương trình tổng quát

$\overrightarrow {AB} = \left( {1,1} \right)$ $\overrightarrow {AB} = \left( {1,1} \right)$

Phương trình tham số: $\frac{{x - 1}}{1} = \frac{{y - 2}}{1}$ $\frac{{x - 1}}{1} = \frac{{y - 2}}{1}$

$\overrightarrow n = \left( { - 1,1} \right)$ $\overrightarrow n = \left( { - 1,1} \right)$

Phương trình tổng quát:

$\begin{matrix} - 1.\left( {x - 1} \right) + 1.\left( {y - 2} \right) = 0 \hfill \\ \Rightarrow y = x + 1 \hfill \\ \end{matrix}$ $\begin{matrix} - 1.\left( {x - 1} \right) + 1.\left( {y - 2} \right) = 0 \hfill \\ \Rightarrow y = x + 1 \hfill \\ \end{matrix}$

$\overrightarrow {AB} = \left( {1,1} \right)$ $\overrightarrow {AB} = \left( {1,1} \right)$

Phương trình tham số: $\frac{{x - 1}}{1} = \frac{{y - 2}}{1}$ $\frac{{x - 1}}{1} = \frac{{y - 2}}{1}$

Gọi phương trình tổng quát là:

y = ax + b

Do PTĐT đi qua 2 điểm A, B nên ta có:
$\left\{ {\begin{array}{*{20}{c}} {2 = a.1 + b} \\ {3 = a.2 + b} \end{array}} \right. \Rightarrow \left( {a;b} \right) = \left( {1;1} \right)$ $\left\{ {\begin{array}{*{20}{c}} {2 = a.1 + b} \\ {3 = a.2 + b} \end{array}} \right. \Rightarrow \left( {a;b} \right) = \left( {1;1} \right)$

Vậy PT tổng quát cần tìm là: $y = x + 1$

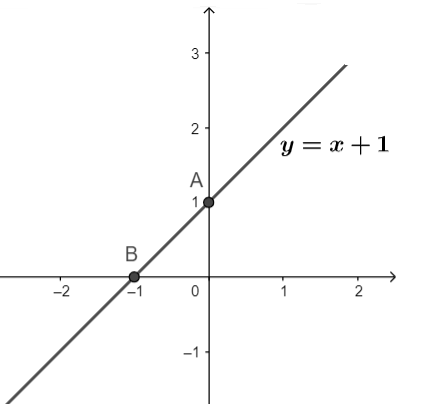
Ví dụ 2: Viết phương trình đường thẳng y = ax + b biết

a) Đi qua 2 điểm A(-3,2), B (5,-4). Tính diện tích tam giác được tạo bởi đường thẳng và 2 trục tọa độ.

b) Đi qua A (3,1) song song với đường thẳng y = -2x + m -1

Hướng dẫn giải

a. Gọi phương trình tổng quát là: y = ax + b

Do PTĐT đi qua 2 điểm A, B nên ta có:

$\left\{ {\begin{array}{*{20}{c}} {2 = - 3a + b} \\ { - 4 = 5a + b} \end{array}} \right. \Rightarrow \left( {a;b} \right) = \left( { - \frac{3}{4}; - \frac{1}{4}} \right)$ $\left\{ {\begin{array}{*{20}{c}} {2 = - 3a + b} \\ { - 4 = 5a + b} \end{array}} \right. \Rightarrow \left( {a;b} \right) = \left( { - \frac{3}{4}; - \frac{1}{4}} \right)$

Vậy PT tổng quát cần tìm là: $y = - \frac{3}{4}x - \frac{1}{4}$ $y = - \frac{3}{4}x - \frac{1}{4}$

Giao điểm của đường thẳng với trục Ox là: $y = 0 \Rightarrow x = - \frac{1}{3} \Rightarrow A\left( { - \frac{1}{3};0} \right)$ $y = 0 \Rightarrow x = - \frac{1}{3} \Rightarrow A\left( { - \frac{1}{3};0} \right)$

$\Rightarrow \overrightarrow {OA} = \left( { - \frac{1}{3};0} \right) \Rightarrow \left| {\overrightarrow {OA} } \right| = \frac{1}{3}$ $\Rightarrow \overrightarrow {OA} = \left( { - \frac{1}{3};0} \right) \Rightarrow \left| {\overrightarrow {OA} } \right| = \frac{1}{3}$

Giao điểm của đường thẳng với trục Oy là: $x = 0 \Rightarrow y = - \frac{1}{4} \Rightarrow B\left( {0; - \frac{1}{4}} \right)$ $x = 0 \Rightarrow y = - \frac{1}{4} \Rightarrow B\left( {0; - \frac{1}{4}} \right)$

$\Rightarrow \overrightarrow {OB} = \left( {0; - \frac{1}{4}} \right) \Rightarrow \left| {\overrightarrow {OB} } \right| = \frac{1}{4}$ $\Rightarrow \overrightarrow {OB} = \left( {0; - \frac{1}{4}} \right) \Rightarrow \left| {\overrightarrow {OB} } \right| = \frac{1}{4}$

$\Rightarrow {S_{OAB}} = \frac{1}{2}.OA.OB = \frac{1}{2}.\frac{1}{3}.\frac{1}{4} = \frac{1}{{24}}$ $\Rightarrow {S_{OAB}} = \frac{1}{2}.OA.OB = \frac{1}{2}.\frac{1}{3}.\frac{1}{4} = \frac{1}{{24}}$

b. Gọi phương trình tổng quát là: y = ax + b

Do đường thẳng song song với y = -2x + m -1

⇒ a = -2

Phương trình đường thẳng trở thành y = -2x + b

Mà đường thẳng qua điểm A(3; 1)

⇒ 1 = 3.(-2) + b
⇒ b = 7

Vậy phương trình tổng quát là: y = -2x + 7

Ví dụ 3: Tìm m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = 2x³ + 3(m - 1)x² + 6(m - 2)x - 1 song song với đường thẳng y = -4x + 1.

Lời giải

Ta có y' = 6x² + 6(m - 1)x + 6(m - 2)

Hàm số có cực trị ⇔ y' = 0 có 2 nghiệm phân biệt

⇔ Δ' > 0 ⇔ 9(m - 1)² - 36(m - 2) > 0 ⇔ 9(m - 3)² > 0 ⇔ m ≠ 3

Thực hiện phép chia y cho y' ta có phương trình đường thẳng đi qua 2 điểm cực trị là:

d: y = (-m2 + 6m - 9)x - m² + 3m - 3

Khi đó d song song với đường thẳng y = -4x + 1. $\Leftrightarrow \left\{ \begin{gathered} - {m^2} + 6m - 9 = - 4 \hfill \\ - {m^2} + 3m - 3 \ne 1 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} m = 1 \hfill \\ m = 5 \hfill \\ \end{gathered} \right. \hfill \\ {m^2} - 3m + 4 \ne 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m = 1 \hfill \\ m = 5 \hfill \\ \end{gathered} \right.$ $\Leftrightarrow \left\{ \begin{gathered} - {m^2} + 6m - 9 = - 4 \hfill \\ - {m^2} + 3m - 3 \ne 1 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} m = 1 \hfill \\ m = 5 \hfill \\ \end{gathered} \right. \hfill \\ {m^2} - 3m + 4 \ne 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m = 1 \hfill \\ m = 5 \hfill \\ \end{gathered} \right.$

Kết hợp với điều kiện ta có m = 1 hoặc m = 5 thỏa mãn

Vậy m = 1 hoặc m = 5 là các giá trị cần tìm.

Ví dụ 4: Trong mặt phẳng với hệ tọa độ $Oxy$, cho tam giác $ABC$ có phương trình cạnh $AB$ là $x - y - 2 = 0$, phương trình cạnh $AC$ là $x + 2y - 5 = 0$. Biết trọng tâm của tam giác là điểm $G(3;2)$ và phương trình đường thẳng $BC$ có dạng $x + my + n = 0$. Tính giá trị biểu thức $S = m + n$.

Hướng dẫn giải

Tọa độ điểm A là nghiệm của hệ phương trình

$\left\{ \begin{matrix} x - y - 2 = 0 \\ x + 2y - 5 = 0 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 3 \\ y = 1 \\ \end{matrix} \right.\ \Leftrightarrow A(3;1)$ $\left\{ \begin{matrix} x - y - 2 = 0 \\ x + 2y - 5 = 0 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 3 \\ y = 1 \\ \end{matrix} \right.\ \Leftrightarrow A(3;1)$

Ta có $B\left( x_{B};x_{B} - 2 \right);C\left( x_{C};\frac{- x_{C} + 5}{2} \right)$ $B\left( x_{B};x_{B} - 2 \right);C\left( x_{C};\frac{- x_{C} + 5}{2} \right)$

Gọi $M\left( x_{0};y_{0} \right)$ $M\left( x_{0};y_{0} \right)$ là trung điểm của BC thì $2\overrightarrow{GM} = \overrightarrow{AG}$ $2\overrightarrow{GM} = \overrightarrow{AG}$ nên

$\left\{ \begin{matrix} 2\left( x_{0} - 3 \right) = 0 \\ 2\left( y_{0} - 2 \right) = 1 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{0} = 3 \\ y_{0} = \dfrac{5}{2} \\ \end{matrix} \right.$ $\left\{ \begin{matrix} 2\left( x_{0} - 3 \right) = 0 \\ 2\left( y_{0} - 2 \right) = 1 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{0} = 3 \\ y_{0} = \dfrac{5}{2} \\ \end{matrix} \right.$

Mặt khác $\left\{ \begin{matrix} x_{B} + x_{C} = 2x_{0} \\ x_{B} - 2 + \dfrac{- x_{C} + 5}{2} = 2y_{0} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{B} + x_{C} = 6 \\ 2x_{B} - x_{C} = 9 \\ \end{matrix} \right.$ $\left\{ \begin{matrix} x_{B} + x_{C} = 2x_{0} \\ x_{B} - 2 + \dfrac{- x_{C} + 5}{2} = 2y_{0} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x_{B} + x_{C} = 6 \\ 2x_{B} - x_{C} = 9 \\ \end{matrix} \right.$

$\Leftrightarrow \left\{ \begin{matrix} x_{B} = 5 \\ x_{C} = 1 \\ \end{matrix} \right.\ \Rightarrow B(5;3),C(1;2)$ $\Leftrightarrow \left\{ \begin{matrix} x_{B} = 5 \\ x_{C} = 1 \\ \end{matrix} \right.\ \Rightarrow B(5;3),C(1;2)$

$\Rightarrow \overrightarrow{BC} = ( - 4; - 1)$ $\Rightarrow \overrightarrow{BC} = ( - 4; - 1)$

Suy ra một vectơ pháp tuyến của BC là $\overrightarrow{n} = (1; - 4)$ $\overrightarrow{n} = (1; - 4)$

Suy ra phương trình đường thẳng BC là

$1(x - 5) - 4(y - 3) = 0$

$\Leftrightarrow x - 4y + 7 = 0$ $\Leftrightarrow x - 4y + 7 = 0$

Suy ra $m = - 4;n = 7 \Rightarrow S = 3$ $m = - 4;n = 7 \Rightarrow S = 3$

Ví dụ 5: Cho hai điểm $C(2;3),D(1;4)$. Viết phương trình đường thẳng cách đều hai điểm $C,D$?

Hướng dẫn giải

Gọi đường thẳng cần tìm là đường thẳng d.

Khi đó đường thẳng d cách đều hai điểm C và D khi:

TH1: Đường thẳng đó song song hoặc trùng với đường thẳng CD,

Ta có: $\overrightarrow{CD} = ( - 1;1)$ $\overrightarrow{CD} = ( - 1;1)$ nên một vectơ pháp tuyến của CD là $\overrightarrow{n} = (1;1)$ $\overrightarrow{n} = (1;1)$

Vậy trong các đường thẳng đã cho chỉ có đường thẳng $x + y - 1 = 0$.

TH2: d là đường trung trực của CD.

Khi đó d đi qua trung điểm $I\left( \frac{3}{2};\frac{7}{2} \right)$ $I\left( \frac{3}{2};\frac{7}{2} \right)$ của CD và nhận $\overrightarrow{CD} = ( - 1;1)$ $\overrightarrow{CD} = ( - 1;1)$ làm VTPT.

Suy ra phương trình đường thẳng d là:

$- 1\left( x - \frac{3}{2} \right) + 1\left( y - \frac{7}{2} \right) = 0$ $- 1\left( x - \frac{3}{2} \right) + 1\left( y - \frac{7}{2} \right) = 0$

$\Leftrightarrow - x + y - 2 = 0$ $\Leftrightarrow - x + y - 2 = 0$

Vậy đáp án là $x + y - 1 = 0$.

5. Bài tập rèn luyện viết phương trình đường thẳng

Câu 1: Phương trình đường thẳng đi qua hai điểm $A( - 2;4)\ ;B( - 6;1)$ $A( - 2;4)\ ;B( - 6;1)$ là:

A. $3x + 4y - 10 = 0.$ B. $3x - 4y + 22 = 0.$

C. $3x - 4y + 8 = 0.$ D. $3x - 4y - 22 = 0$.

Câu 2: Cho tam giác $ABC$ có $A( - 1; - 2);B(0;2);C( - 2;1)$. Đường trung tuyến $BM$ có phương trình là:

A. $5x - 3y + 6 = 0$ B. $3x - 5y + 10 = 0$

C. $x - 3y + 6 = 0$. D. $3x - y - 2 = 0$

Câu 3. Phương trình tổng quát của đường thẳng đi qua hai điểm $A( - 2;4),B(1;0)$ là

A. $4x + 3y + 4 = 0.$ B. $4x + 3y - 4 = 0.$

C. $4x - 3y + 4 = 0.$ D.$4x - 3y - 4 = 0.$

Câu 4. Viết phương trình tham số của đường thẳng đi qua hai điểm $A(2; - 1)$ và $B(2;5)$.

A. $\left\{ \begin{matrix} x = 2 \\ y = - 1 + 6t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 2 \\ y = - 1 + 6t \end{matrix} \right.\ .$ B. $\left\{ \begin{matrix} x = 2t \\ y = - 6t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 2t \\ y = - 6t \end{matrix} \right.\ .$ C. $\left\{ \begin{matrix} x = 2 + t \\ y = 5 + 6t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 2 + t \\ y = 5 + 6t \end{matrix} \right.\ .$ D. $\left\{ \begin{matrix} x = 1 \\ y = 2 + 6t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 1 \\ y = 2 + 6t \end{matrix} \right.\ .$

Câu 5. Viết phương trình đường thẳng đi qua 2 điểm $A(0; - 5)$ và $B(3;0)$.

A. $\frac{x}{5} + \frac{y}{3} = 1$ $\frac{x}{5} + \frac{y}{3} = 1$. B. $- \frac{x}{5} + \frac{y}{3} = 1$ $- \frac{x}{5} + \frac{y}{3} = 1$. C. $\frac{x}{3} - \frac{y}{5} = 1$ $\frac{x}{3} - \frac{y}{5} = 1$. D. $\frac{x}{3} - \frac{y}{5} = 0$ $\frac{x}{3} - \frac{y}{5} = 0$.

Câu 6. Viết phương trình tham số của đường thẳng đi qua hai điểm $A(2; - 1)$ và $B(2;5)$.

A. $\left\{ \begin{matrix} x = 2 \\ y = - 1 + 6t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 2 \\ y = - 1 + 6t \end{matrix} \right.\ .$ B. $\left\{ \begin{matrix} x = 2t \\ y = - 6t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 2t \\ y = - 6t \end{matrix} \right.\ .$ C. $\left\{ \begin{matrix} x = 2 + t \\ y = 5 + 6t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 2 + t \\ y = 5 + 6t \end{matrix} \right.\ .$ D. $\left\{ \begin{matrix} x = 1 \\ y = 2 + 6t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 1 \\ y = 2 + 6t \end{matrix} \right.\ .$

Câu 7. Viết phương trình tham số của đường thẳng đi qua hai điểm $A( - 1\ ;\ 3)$ $A( - 1\ ;\ 3)$ và $B(3\ ;\ 1)$ $B(3\ ;\ 1)$.

A. $\left\{ \begin{matrix} x = - 1 + 2t \\ y = 3 + t \end{matrix} \right.$ $\left\{ \begin{matrix} x = - 1 + 2t \\ y = 3 + t \end{matrix} \right.$. B. $\left\{ \begin{matrix} x = - 1 - 2t \\ y = 3 - t \end{matrix} \right.$ $\left\{ \begin{matrix} x = - 1 - 2t \\ y = 3 - t \end{matrix} \right.$. C. $\left\{ \begin{matrix} x = 3 + 2t \\ y = - 1 + t \end{matrix} \right.$ $\left\{ \begin{matrix} x = 3 + 2t \\ y = - 1 + t \end{matrix} \right.$. D. $\left\{ \begin{matrix} x = - 1 - 2t \\ y = 3 + t \end{matrix} \right.$ $\left\{ \begin{matrix} x = - 1 - 2t \\ y = 3 + t \end{matrix} \right.$.

Câu 8. Đường thẳng đi qua hai điểm $A(1;1)$ và $B(2;2)$ có phương trình tham số là:

A. $\left\{ \begin{matrix} x = 1 + t \\ y = 2 + 2t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 1 + t \\ y = 2 + 2t \end{matrix} \right.\ .$ B. $\left\{ \begin{matrix} x = 1 + t \\ y = 1 + 2t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 1 + t \\ y = 1 + 2t \end{matrix} \right.\ .$ C. $\left\{ \begin{matrix} x = 2 + 2t \\ y = 1 + t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = 2 + 2t \\ y = 1 + t \end{matrix} \right.\ .$ D. $\left\{ \begin{matrix} x = t \\ y = t \end{matrix} \right.\ .$ $\left\{ \begin{matrix} x = t \\ y = t \end{matrix} \right.\ .$

Câu 9. Đường thẳng đi qua hai điểm $A(3;-7)$ và $B(1; - 7)$ có phương trình tham số là:

A. $\left\{ \begin{matrix} x = t \\ y = - 7 \end{matrix} \right.$ $\left\{ \begin{matrix} x = t \\ y = - 7 \end{matrix} \right.$. B. $\left\{ \begin{matrix} x = t \\ y = - 7 - t \end{matrix} \right.$ $\left\{ \begin{matrix} x = t \\ y = - 7 - t \end{matrix} \right.$. C. $\left\{ \begin{matrix} x = 3 - t \\ y = 1 - 7t \end{matrix} \right.$ $\left\{ \begin{matrix} x = 3 - t \\ y = 1 - 7t \end{matrix} \right.$. D. $\left\{ \begin{matrix} x = t \\ y = 7 \end{matrix} \right.$ $\left\{ \begin{matrix} x = t \\ y = 7 \end{matrix} \right.$.

Câu 10. Phương trình nào dưới đây không phải là phương trình tham số của đường thẳng đi qua hai điểm $O(0;0)$ và $M(1; - 3)$?

A. $\left\{ \begin{matrix} x = 1 - t \\ y = 3t \end{matrix} \right.$ $\left\{ \begin{matrix} x = 1 - t \\ y = 3t \end{matrix} \right.$. B. $\left\{ \begin{matrix} x = 1 + t \\ y = - 3 - 3t \end{matrix} \right.$ $\left\{ \begin{matrix} x = 1 + t \\ y = - 3 - 3t \end{matrix} \right.$. C. $\left\{ \begin{matrix} x = 1 - 2t \\ y = - 3 + 6t \end{matrix} \right.$ $\left\{ \begin{matrix} x = 1 - 2t \\ y = - 3 + 6t \end{matrix} \right.$. D. $\left\{ \begin{matrix} x = - t \\ y = 3t \end{matrix} \right.$ $\left\{ \begin{matrix} x = - t \\ y = 3t \end{matrix} \right.$.

Câu 11. Phương trình tổng quát của đường thẳng đi qua hai điểm $A(3; - 1)$ và $B(1;5)$ là:

A. $- x + 3y + 6 = 0.$ B. $3x - y + 10 = 0.$

C. $3x - y + 6 = 0.$ D. $3x + y - 8 = 0.$

Câu 12. Phương trình tổng quát của đường thẳng đi qua hai điểm $A(2; - 1)$ và $B(2;5)$ là:

A. $x + y - 1 = 0.$ B. $2x - 7y + 9 = 0.$ C. $x + 2 = 0.$ D. $x - 2 = 0.$

Câu 13. Phương trình tổng quát của đường thẳng đi qua hai điểm $A(3; - 7)$ và $B(1; - 7)$ là:

A. $y - 7 = 0.$ B. $y + 7 = 0.$ C. $x + y + 4 = 0.$ D. $x + y + 6 = 0.$

-----------------------------------------------------------------------

Trên đây là toàn bộ hướng dẫn chi tiết về cách viết phương trình đường thẳng đi qua 2 điểm, kèm theo ví dụ minh họa rõ ràng và công thức dễ nhớ. Việc nắm vững kiến thức này không chỉ giúp bạn tự tin giải bài tập trong sách giáo khoa mà còn hỗ trợ hiệu quả cho các đề thi nâng cao hoặc đề kiểm tra năng lực. Để học tốt hơn, bạn hãy luyện tập thêm nhiều bài tập khác nhau, thử thay đổi tọa độ hai điểm và viết ra nhiều phương trình đường thẳng khác nhau. Nhờ đó, bạn sẽ rèn luyện khả năng tư duy và phản xạ nhanh với mọi dạng bài.

Hy vọng bài viết “Phương trình đường thẳng đi qua 2 điểm” này đã giúp bạn nắm vững phương pháp và tự tin áp dụng trong học tập. Đừng quên chia sẻ cho bạn bè và theo dõi những bài viết tiếp theo để cập nhật thêm nhiều kiến thức Toán học hữu ích nhé!

Tải về

Chọn file muốn tải về: