Dấu của nhị thức bậc nhất

Chuyên đề Toán học lớp 10: Dấu của nhị thức bậc nhất được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo.

I. ĐỊNH LÍ VỀ DẤU CỦA NHỊ THỨC BẬC NHẤT

1. Nhị thức bậc nhất

Nhị thức bậc nhất đối với x là biểu thức dạng f(x) = ax + b trong đó a, b là hai số đã cho, a ≠ 0.

2. Dấu của nhị thức bậc nhất

Định lí

Nhị thức f(x) = ax + b có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng (-; +∞), trái dấu với hệ số a khi x lấy giá trị trong khoảng (-∞; -)

x	-∞ - +∞
f(x) = ax + b	trái dấu với a 0 cùng dấu với a

II. XÉT DẤU TÍCH, THƯƠNG CÁC NHỊ THỨC BẬC NHẤT

Giả sử f(x) là một tích của những nhị thức bậc nhất. Áp dụng định lí về dấu của nhị thức bậc nhất có thể xét dấu từng nhân tử. Lập bảng xét dấu chung cho tất cả các nhị thức bậc nhất có mặt trong f(x) ta suy ra được dấu của f(x). Trường hợp f(x) là một thương cũng được xét tương tự.

III. ÁP DỤNG VÀO GIẢI BẤT PHƯƠNG TRÌNH

Giải bất phương trình f(x) > 0 thực chất là xét xem biểu thức f(x) nhận giá trị dương với những giá trị nào của x (do đó cũng biết f(x) nhận giá trị âm với những giá trị nào của x), làm như vậy ta nói đã xét dấu biểu thức f(x).

1. Bất phương trình tích, bất phương trình chứa ẩn ở mẫu thức

Ví dụ. Giải bất phương trình ≥ 1.

Giải.

Ta biến đổi tương đương bất phương trình đã cho

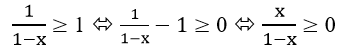
Xét dấu biểu thức f(x) =

Ta suy ra nghiệm của bất phương trình đã cho là 0 ≤ x < 1.

2. Bất phương trình chứa ẩn trong dấu giá trị tuyệt đối

Ví dụ. Giải bất phương trình |–2x + 1| – x – 3 < 5.

Giải.

Theo định nghĩa giá trị tuyệt đối, ta có

Tổng hợp lại tập nghiệm của bất phương trình đã cho là hợp của hai khoảng (–7; ] và (; 3).

Kết luận. Bất phương trình đã cho có nghiệm là –7 < x < 3.

Bằng cách áp dụng tính chất của giá trị tuyệt đối ta có thể dễ dàng giải các bất phương trình dạng |f(x)| ≤ a và |f(x)| ≥ a với a > 0 đã cho.

Ta có

|f(x)| ≤ a <=> –a ≤ f(x) ≤ a

|f(x)| ≥ a <=> f(x) ≤ –a hoặc f(x) ≥ a (a > 0)

Với nội dung bài Dấu của nhị thức bậc nhất trên đây chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững khái niệm, định lý của dấu nhị thức bậc nhất...

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Dấu của nhị thức bậc nhất. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc