Ứng dụng của hàm số bậc hai trong chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất
Chuyên đề Toán học lớp 10: Ứng dụng của hàm số bậc hai trong chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo.
Bài: Ứng dụng của hàm số bậc hai trong chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất
1. Phương pháp giải.
Dựa vào đồ thị (bảng biến thiên) của hàm số y = ax2 + bx + c, a ≠ 0 ta thấy nó đạt giá trị lớn nhất, nhỏ nhất trên [α; β] tại điểm x = α hoặc x = β hoặc x = -b/(2a). Cụ thể:
TH 1: a > 0
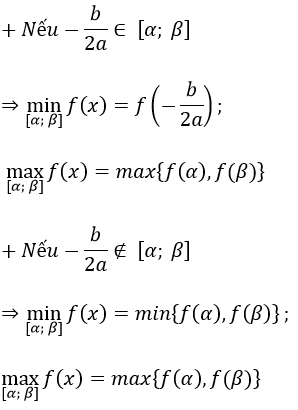
TH 2: a < 0:
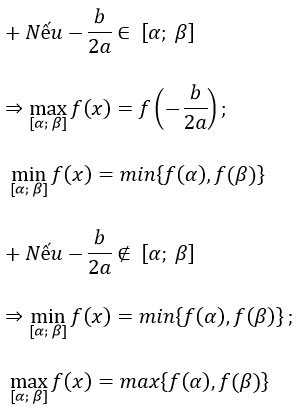
2. Các ví dụ minh họa.
Ví dụ 1: Cho phương trình x2 + 2(m + 3)x + m2 - 3 = 0, m là tham số.
Tìm m để phương trình có hai nghiệm x1; x2 và P = 5(x1 + x2 ) - 2x1x2 đạt giá trị lớn nhất.
Hướng dẫn:
Ta có Δ' = (m + 3)2 - (m2 - 3) = 6m + 12
Phương trình có nghiệm ⇔ Δ' ≥ 0 ⇔ 6m + 12 ≥ 0 ⇔ m ≥ -2
Theo định lý Viét ta có:
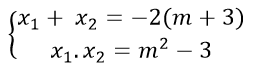
P = 5(x1 + x2) - 2x1x2 = -10(m + 3) - 2(m2 - 3) = -2m2 - 10m - 24.
Xét hàm số f(m) = -2m2 - 10m - 24 với m ∈ [-2; +∞)
Bảng biến thiên
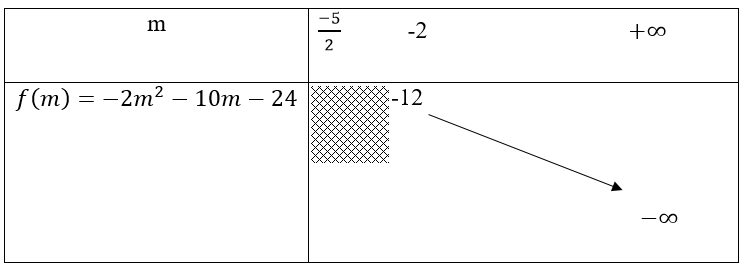
Suy ra![]() khi và chỉ khi m = -2
khi và chỉ khi m = -2
Vậy m = -2 là giá trị cần tìm.
Ví dụ 2: Tìm giá trị nhỏ nhất của hàm số:
![]()
Hướng dẫn:
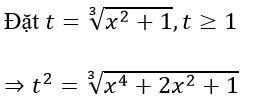
Khi đó hàm số trở thành y = t2 - 3t + 1 với t ≥ 1
Bảng biến thiên
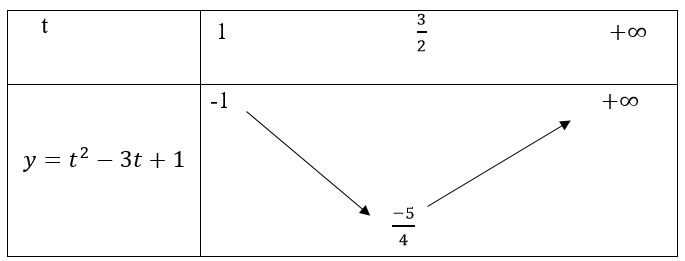
Suy ra giá trị nhỏ nhất của hàm số y = t2 - 3t + 1 là (-5)/4 khi và chỉ khi t = 3/2 hay
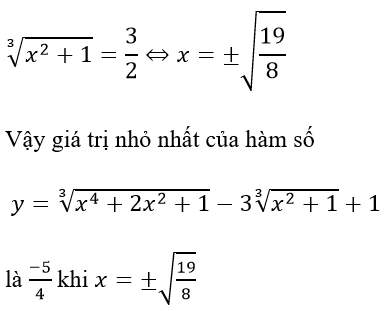
Ví dụ 3: Cho các số thực a, b thoả mãn ab ≠ 0 . Tìm giá trị nhỏ nhất của biểu thức
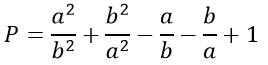
Hướng dẫn:
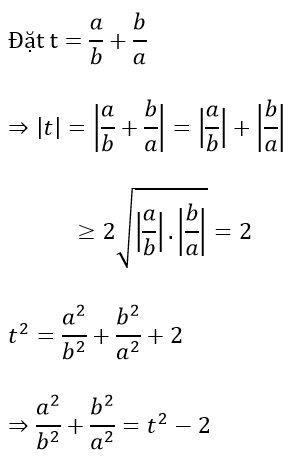
Ta có P = t2 - 2 - t + 1 = t2 - t - 1
Xét hàm số f(t) = t2 - t - 1 với t ∈ (-∞;-2] ∪ [2; +∞)
Bảng biến thiên
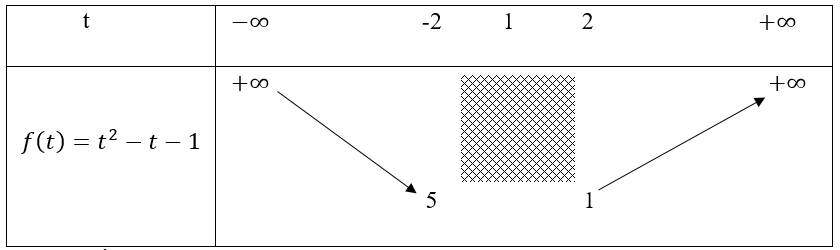
Từ bảng biến thiên ta có:
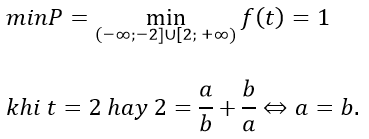
Với nội dung bài Ứng dụng của hàm số bậc hai trong chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất trên đây chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững phương pháp giải, chứng minh bất đẳng thức từ hàm số bậc hai....
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Ứng dụng của hàm số bậc hai trong chứng minh bất đẳng thức và tìm giá trị nhỏ nhất, lớn nhất. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc








