Cho . Điều kiện cần và đủ để
là:
Ta có:
.
Các phép toán trên tập hợp chứa tham số là dạng bài tập nâng cao trong chương trình Toán lớp 10, thường gây khó khăn cho học sinh do vừa yêu cầu kiến thức về tập hợp, vừa phải giải phương trình hoặc bất phương trình theo tham số. Việc thành thạo các phép toán như giao, hợp, hiệu, phần bù trong điều kiện chứa tham số sẽ giúp học sinh xử lý bài toán chính xác, nhanh chóng. Trong bài viết này, bạn sẽ được ôn tập lý thuyết trọng tâm và luyện tập với các bài tập tập hợp có tham số kèm đáp án và lời giải chi tiết, giúp hiểu sâu và vận dụng linh hoạt trong các đề kiểm tra và đề thi học kỳ.
Cho . Điều kiện cần và đủ để
là:
Ta có:
.
Cho số thực . Tìm
để
.
Để thì giá trị của số thực
phải thỏa bất phương trình
.
Ta có (do
)
.
So điều kiện , suy ra
.
Cho tập hợp với m là tham số. Điều kiện để
là:
Ta có:
Cho hai tập hợp . Điều kiện để
là:
Biểu diễn tập số trên trục số:

Điều kiện để là
.
Cho 2 tập hợp khác rỗng ,
, với
. Tìm
để
.
Với 2 tập hợp khác rỗng ,
ta có điều kiện
.
.
.
Kết hợp với điều kiện .
Cho số thực . Điều kiện cần và đủ để
là:
Ta có:
.
Cho hai tập ;
,
. Với giá trị nào của
thì
?
Ta tìm
Cho hai tập hợp . Tìm tất cả các giá trị của m để
.
Biểu diễn tập hợp trên trục số như sau:
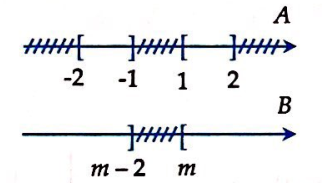
Giải bất phương trình:
Để thì:
Cho tập hợp . Điều kiện để
là:
Ta có:
Cho tập hợp . Tìm điều kiện của m để
.
Biểu diễn tập hợp trên trục số:
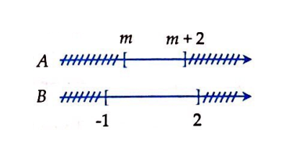
Để thì
Cho hai tập hợp khác rỗng và
,
. Tìm tất cả các giá trị của
để
.
Điều kiện để hai tập và
khác tập rỗng là
.
Khi đó
Cho tập hợp và
. Tìm m để B có đúng hai tập con và
.
Để B có đúng hai tập con thì B phải có duy nhất một phần tử, và nên B có một phần tử thuộc A.
Tóm lại ta tìm m để phương trình (1) có nghiệm duy nhất lớn hơn 0.
+ Với ta có phương trình:
(không thỏa mãn).
+ Với :
Phương trình (1) có nghiệm duy nhất lớn hơn 0 điều kiện cần là:
+) Với ta có phương trình
Phương trình có nghiệm (không thỏa mãn).
+) Với , ta có phương trình
Phương trình có nghiệm duy nhất thỏa mãn.
Cho hai tập ;
,
. Với giá trị nào của
thì
.
Trước hết tìm để
. Với
.
Ta có .
Từ đó, kết hợp điều kiện ta có .
Cho số thực . Điều kiện cần và đủ để
là:
Ta có:
.
Cho hai tập hợp ,
. Tìm m để
.
Biểu diễn tập hợp trên trục số
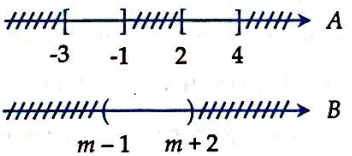
Ta đi tìm m để
hay
Cho hai tập hợp và
. Tìm tất cả các giá trị của
để
.
Vậy đáp án cần tìm là:
Cho ;
. Có bao nhiêu giá trị nguyên
thỏa
Ta có:
Để thì
Khi đó
.
Vậy có 3989 giá trị nguyên thỏa mãn.
Cho 2 tập khác rỗng . Tìm m để
Đáp án đúng vì: Với 2 tập khác rỗng A, B ta có điều kiện
.
Để .
So với kết quả của điều kiện thì .
Cho 3 tập hợp ,
,
. Tìm m để
.
Biểu diễn tập hợp trên trục số

Ta đi tìm m để
- TH1: Nếu thì
- TH2: Nếu
Vì nên

Cho . Tìm
để
Ta có:
.
Tìm để
, biết
và
.
Ta có:
.
Cho hai tập hợp và
. Tìm tất cả các giá trị của
để
.
Biểu diễn tập số trên trục số như sau:

là
.
Cho hai tập hợp khác rỗng và
Có bao nhiêu giá trị nguyên dương của
để
?
Ta có là hai tập khác rỗng nên
(*).
Ta có .
Đối chiếu với điều kiện (*), ta được .
Do nên
.
Vậy có 4 giá trị nguyên dương của thỏa mãn yêu cầu.
Cho 2 tập hợp và
. Tìm tất cả các giá trị thực của tham số
để
.
Ta có .
Để
.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: