Hướng dẫn cách xác định mệnh đề kéo theo và mệnh đề đảo
Mệnh đề kéo theo và mệnh đề đảo Toán 10
Bạn đang muốn làm chủ cách xác định mệnh đề kéo theo và mệnh đề đảo trong Logic học và Toán học? Đây là hai khái niệm nền tảng, thiết yếu để bạn xây dựng các suy luận chặt chẽ, chứng minh định lý và giải quyết các bài toán phức tạp. Bài viết này sẽ cung cấp cho bạn một hướng dẫn chi tiết, từ định nghĩa rõ ràng, các ví dụ minh họa cụ thể đến những lưu ý quan trọng giúp bạn xác định mệnh đề kéo theo (nếu... thì...) và mệnh đề đảo một cách chính xác nhất. Đừng bỏ lỡ cơ hội củng cố kiến thức logic và nâng cao kỹ năng giải toán của bạn ngay hôm nay!
A. Mệnh đề kéo theo
Định nghĩa:
Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo và kí hiệu là 
\(P \Rightarrow Q\).
Mệnh đề \(P \Rightarrow Q\) còn được phát biểu là “\(P\) kéo theo \(Q\)” hoặc “Từ \(P\) suy ra \(Q\)”
Chú ý:
- Mệnh đề \(P \Rightarrow Q\) chỉ sai khi \(P\) đúng \(Q\) sai.
- Ta chỉ xét tính đúng sai của mệnh đề \(P
\Rightarrow Q\) khi \(P\) đúng.
- Khi đó, nếu \(Q\) đúng thì \(P \Rightarrow Q\) đúng, nếu \(Q\) sai thì \(P
\Rightarrow Q\) sai.
- Các định lí toán học là những mệnh đề đúng và có dạng \(P \Rightarrow Q.\)
- Khi đó \(P\) là giả thiết, \(Q\) là kết luận của định lí hoặc \(P\) là điều kiện đủ để có \(Q\) hoặc \(Q\) là điều kiện cần để có \(P.\)
Cách xác định mệnh đề kéo theo
Bảng logic xét tính đúng sai của mệnh đề kéo theo (bảng chân trị):
| \(P\) |
\(Q\) |
\(P \Rightarrow Q\) |
|
Đúng |
Đúng |
Đúng |
|
Đúng |
Sai |
Sai |
|
Sai |
Đúng |
Đúng |
|
Sai |
Sai |
Đúng |
Các bước để xác định một mệnh đề kéo theo và tính đúng sai của nó ta làm theo các bước sau:
- Bước 1. Xác định rõ ràng hai mệnh đề P và Q.
- Phần đứng sau “Nếu” hoặc là điều kiện được đặt ra chính là mệnh đề P.
- Phần đứng sau “thì” hoặc là hệ quả suy ra chính là mệnh đề Q.
- Bước 2. Xác định tính đúng sai của từng mệnh đề P và Q một cách độc lập.
- P đúng hay sai?
- Q đúng hay sai?
- Bước 3. Áp dụng bảng logic để kết luận tính đúng sai của mệnh đề kéo theo P ⇒ Q.
Ví dụ. Cho tứ giác \(ABCD\), xét hai câu sau:
\(P\) : “Tứ giác \(ABCD\) có tổng số đo hai góc đối diện bằng \(180^{{^\circ}}\) "
Q: “ABCD là tứ giác nội tiếp đường tròn".
Phát biểu mệnh đề \(P \Rightarrow
Q\) và cho biết tính đúng sai của mệnh đề đó.
Hướng dẫn giải
Hình vẽ minh họa
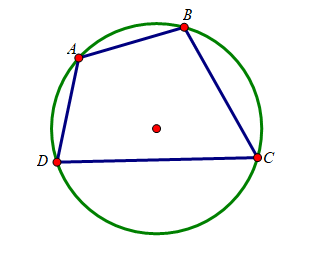
\(P \Rightarrow Q\) : "Nếu tứ giác \(ABCD\) có tổng số đo hai góc đối diện bằng \(180^{{^\circ}}\) thì \(ABCD\) là tứ giác nội tiếp đường tròn".
Mệnh đề kéo theo này là mệnh đề đúng.
Chú ý: Các định lí toán học thường có dạng \(P \Rightarrow Q\). Khi đó:
- P là giả thiết, Q là kết luận.
- P là điều kiện đủ để có Q.
- Q là điều kiện cần để có P.
B. Mệnh đề đảo
Định nghĩa
Cho mệnh đề kéo theo \(P \Rightarrow
Q\). Mệnh đề \(Q \Rightarrow P\) được gọi là mệnh đề đảo của mệnh đề \(P
\Rightarrow Q\).
Nhận xét. Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
Cách xác định mệnh đề đảo
- Bước 1. Xác định rõ ràng giả thiết (P) và kết luận (Q) của mệnh đề kéo theo gốc.
- Tìm phần đứng sau “Nếu” hoặc là điều kiện ban đầu (đó là P).
- Tìm phần đứng sau “thì” hoặc là hệ quả (đó là Q).
- Bước 2: Đổi chỗ giả thiết (P) và kết luận (Q) cho nhau, sau đó viết lại mệnh đề dưới dạng “Nếu Q thì P”.
Ví dụ. Hãy phát biểu mệnh đề đảo của mệnh đề: "Nếu tam giác \(ABC\) là tam giác đều thì tam giác \(ABC\) là tam giác cân" và xác định tính đúng sai của mệnh đề đảo này.
Hướng dẫn giải
Mệnh đề đảo là: "Nếu tam giác \(ABC\) là tam giác cân thì tam giác \(ABC\) là tam giác đều".
Mệnh đề đảo này là sai.
C. Bài tập xác định mệnh đề kéo theo và mệnh đề đảo
Bài 1. Cho tam giác \(ABC\). Xét hai mệnh đề sau:
\((P)\): “tam giác \(ABC\) vuông”; \((Q)\): “\(AB^{2}
+ AC^{2} = BC^{2}\)”
Hãy phát biểu thành lời văn mệnh đề sau, và cho biết mệnh đề đó đúng hay sai:
a. \((P) \Rightarrow (Q)\).
b. \((Q) \Rightarrow (P)\).
Bài 2. Cho tứ giác \(ABCD\). Xét hai mệnh đề:
\((P)\) : “Tứ giác \(ABCD\) là hình vuông”
\((Q)\): “Tứ giác \(ABCD\) là hình chữ nhật có hai đường chéo vuông góc”.
Phát biểu \((P) \Rightarrow (Q)\) bằng hai cách, mệnh đề này đúng hay sai?
Bài 3. Cho tam giác \(ABC\). Lập mệnh đề \((P) \Rightarrow (Q)\) và mệnh đề đảo của nó, rồi xét tính đúng sai của chúng khi:
a. \((P):\) “Góc \(A\) bằng \(90^{0}\)” \((Q):\) “Cạnh \(BC\) lớn nhất”.
b. \((P):\) “\(\widehat{A} = \widehat{B}\)” \((Q):\) “Tam giác \(ABC\) cân”.
Bài 4. Mệnh đề sau đúng, sai?
a) Điều kiện cần và đủ để \(a =
0\) là \(\frac{5}{a} =
\frac{5}{b}\).
b) Điều kiện đủ để \(x > y\) là \(\sqrt{x} > \sqrt{y}\).
c) Điều kiện cần để tam giác ABC vuông là \(AB^{2} = BC^{2} - AC^{2}\).
d) Điều kiện đủ để \(\sqrt{x^{2}} =
|x|\) là \(x \geq 0\).
Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!
-------------------------------------------
Qua bài viết này, hy vọng bạn đã nắm vững cách xác định mệnh đề kéo theo và mệnh đề đảo. Việc hiểu rõ mối quan hệ giữa chúng, đặc biệt là sự khác biệt về tính đúng sai, sẽ là chìa khóa để bạn tránh mắc lỗi trong suy luận và chứng minh. Hãy thường xuyên luyện tập với các dạng bài tập khác nhau để củng cố kiến thức và rèn luyện tư duy logic. Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại tìm hiểu thêm từ các nguồn tài liệu uy tín hoặc chia sẻ để chúng ta cùng trao đổi. Nắm vững những khái niệm cơ bản này sẽ là bước đệm vững chắc cho hành trình chinh phục tri thức của bạn trong Toán học và Logic.
