Xét tính chẵn lẻ của hàm số

Chuyên đề môn Toán lớp 10

Chuyên đề Toán học lớp 10: Xét tính chẵn lẻ của hàm số được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo chi tiết bài viết và tải về tại đây nhé.

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THPT miễn phí trên Facebook: Tài liệu học tập lớp 10. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

1. Phương pháp giải.

* Sử dụng định nghĩa

Hàm số y = f(x) xác định trên D

+ Hàm số chẵn 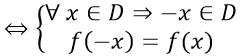chuyên đề toán 10

+ Hàm số lẻ 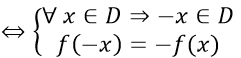chuyên đề toán 10

Chú ý: Một hàm số có thể không chẵn cũng không lẻ

Đồ thị hàm số chẵn nhận trục Oy làm trục đối xứng

Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng

* Quy trình xét hàm số chẵn, lẻ.

B1: Tìm tập xác định của hàm số.

B2: Kiểm tra

Nếu ∀ x ∈ D ⇒ -x ∈ D Chuyển qua bước ba

Nếu ∃ x₀ ∈ D ⇒ -x₀ ∉ D kết luận hàm không chẵn cũng không lẻ.

B3: xác định f(-x) và so sánh với f(x).

Nếu bằng nhau thì kết luận hàm số là chẵn

Nếu đối nhau thì kết luận hàm số là lẻ

Nếu tồn tại một giá trị ∃ x₀ ∈ D mà f(-x₀ ) ≠ ± f(x₀) kết luận hàm số không chẵn cũng không lẻ.

2. Các ví dụ minh họa.

Ví dụ 1: Xét tính chẵn, lẻ của các hàm số sau:

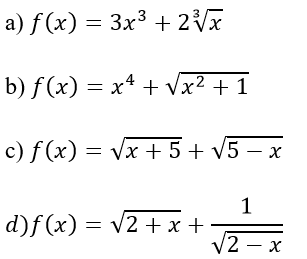
chuyên đề toán 10

Hướng dẫn:

a) f(x) = 3x³ + 2∛x

TXĐ: D = R.

Với mọi x ∈ D, ta có -x ∈ D

f(-x) = 3.(-x)³ + 2∛(-x) = -(3x³ + 2∛x) = -f(x)

Do đó f(x) = 3x³ + 2∛x là hàm số lẻ

b)

TXĐ: D = R.

Với mọi x ∈ D, ta có -x ∈ D

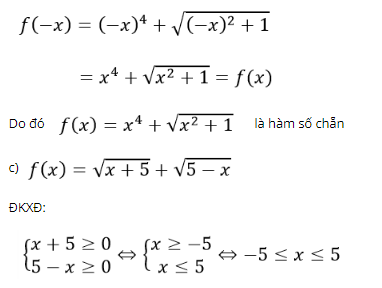
chuyên đề toán 10

Suy ra TXĐ: D = [-5;5]

Với mọi x ∈ [-5;5] ta có -x ∈ [-5;5]

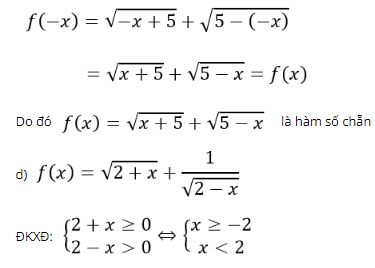
chuyên đề toán 10

Suy ra TXĐ: D = [-2; 2)

Ta có x₀ = -2 ∈ D nhưng -x₀ = 2 ∉ D

Vậy hàm số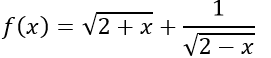 chuyên đề toán 10 không chẵn và không lẻ.

Ví dụ 2: Tìm m để hàm số sau là hàm số chẵn.

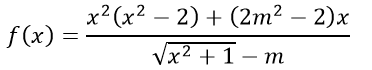
chuyên đề toán 10

Hướng dẫn:

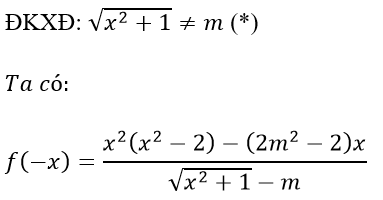
chuyên đề toán 10

Giả sử hàm số chẵn suy ra f(-x) = f(x) với mọi x thỏa mãn điều kiện (*)

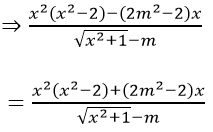
chuyên đề toán 10

với mọi x thỏa mãn (*)

⇒ 2(2m² - 2) x = 0 với mọi x thỏa mãn (*)

⇔ 2m² - 2 = 0 ⇔ m = ± 1

+ Với m = 1 ta có hàm số là

ĐKXĐ : √(x²+1) ≠ 1 ⇔ x ≠ 0

Suy ra TXĐ: D = R\{0}

Dễ thấy với mọi x ∈ R\{0} thì -x ∈ R\{0} và f(-x) = f(x)

Do đólà hàm số chẵn.

+ Với m = -1 ta có hàm số là

TXĐ: D = R

Dễ thấy với mọi x ∈ R thì -x ∈ R và f(-x) = f(x)

Do đólà hàm số chẵn.

Vậy m = ± 1 là giá trị cần tìm.

Bài tập vận dụng

Bài 1: Chứng minh rằng với hàm số f(x) bất kỳ, f(x) có thể biểu diễn duy nhất dưới dạng tổng của một hàm số chẵn và một hàm số lẻ.

Bài 2: Cho hàm số y=f(x), y=g(x) có cùng tập xác định D. Chứng minh rằng:

Nếu hai hàm số trên lẻ thì hàm số y=f(x)+g(x) là hàm số lẻ.

Nếu hai hàm số trên một chẵn, một lẻ thì hàm số y=f(x)g(x) là hàm số lẻ.

Bài 3: Cho hàm số f(x) = (m - 2)x2 + (m - 3)x + m2 - 4

a) Tìm m để hàm f(x) là hàm chẵn

b) Tìm m để hàm f(x) là hàm lẻ.

Bài 4: Khảo sát tính chẵn lẻ của các hàm số có trị tuyệt đối sau

a) f(x) = |2x + 1| + |2x - 1|

b) f(x) = (|x + 1| + |x - 1|)/(|x + 1| - |x - 1|)

a) f(x) = |x - 1|2.

Với nội dung bài Xét tính chẵn lẻ của hàm số trên đây chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững phương pháp giải, công thức tính chẵn lẻ của một hàm số....

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Xét tính chẵn lẻ của hàm số. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc.

Mời các bạn cùng tham khảo thêm các tài liệu về hàm số sau đây được VnDoc.com tổng hợp: