VnDoc.com

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Bài tập Toán 10 Tập hợp con có đáp án chi tiết

Chuyên đề Tập hợp Toán 10 có đáp án

Bài tập Toán 10: Tập hợp - Tập hợp con (Có đáp án chi tiết)

Trong chương trình Toán lớp 10, tập hợp con là phần kiến thức nền tảng, đóng vai trò quan trọng cho nhiều chương học tiếp theo. Tuy nhiên, không ít học sinh vẫn gặp khó khăn trong việc xác định tập hợp con, phân biệt giữa tập rỗng, tập con thực sự và tập hợp bằng nhau. Để giúp các em luyện tập tốt hơn, bài viết này tổng hợp các bài tập Toán 10 về tập hợp con có đáp án chi tiết, kèm lời giải dễ hiểu, giúp học sinh tự ôn tập và nâng cao kỹ năng giải toán hiệu quả.

Nhận biết Thông hiểu

Bài kiểm tra này bao gồm 28 câu
Điểm số bài kiểm tra: 28 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

00:00:00

Câu 1: Nhận biết
Tìm số tập con của tập A
Cho tập hợp $A = \left\{ a,\ b,\ c,\ d \right\}$ . Tập $A$ có mấy tập con?
- A.
  $12$ .
- B.
  $10$ .
- C.
  $15$ .
- D.
  $16$ .
Hướng dẫn:
Số tập hợp con của tập hợp có $4$ phần tử là $2^{4} = 16$ tập hợp con.
Câu 2: Thông hiểu
Tìm mệnh đề sai
Cho hai tập hợp: $X = n\mathbb{\in N}|n\{$ là bội số của 4 và 6} và $Y = n\mathbb{\in N}|n\{$ là bội số của 12}. Trong các mệnh đề sau, tìm mệnh đề sai?
- A.
  $\exists n:\ n \in X$ và $n \notin Y$ .
- B.
  $X = Y$ .
- C.
  $X \subset Y$ .
- D.
  $Y \subset X$ .
Hướng dẫn:
Vì bội số chung nhỏ nhất của 4 và 6 là 12.
Câu 3: Thông hiểu
Tìm số tập con của tập X
Cho tập $X$ có $n + 1$ phần tử ( $n \in \mathbb{N}$ ). Số tập con của $X$ có hai phần tử là
- A.
  $n(n + 1)$ .
- B.
  $\frac{n(n + 1)}{2}$ .
- C.
  $\frac{n(n - 1)}{2}$ .
- D.
  $n + 1$ .
Hướng dẫn:
Lấy một phần tử của $X$ , ghép với $n$ phần tử còn lại được $n$ tập con có hai phần tử. Vậy có $(n + 1)n$ tập.

Nhưng mỗi tập con đó được tính hai lần nên số tập con của $X$ có hai phần tử là $\frac{n(n + 1)}{2}$ .
Câu 4: Thông hiểu
Chọn đáp án đúng
Tập $A = \left\{ 1;2;3;4;5;6 \right\}$ có bao nhiêu tập hợp con có đúng hai phần tử?
- A.
  $3.$
- B.
  $10.$
- C.
  $15.$
- D.
  $30.$
Hướng dẫn:
Các tập con có hai phần tử của tập $A$ là:

$\mathbf{A}_{\mathbf{1}}\mathbf{=}\left\{ \mathbf{1;2} \right\}\mathbf{;}\mathbf{A}_{\mathbf{2}}\mathbf{=}\left\{ \mathbf{1;3} \right\}\mathbf{;}\mathbf{A}_{\mathbf{3}}\mathbf{=}\left\{ \mathbf{1;4} \right\}\mathbf{;}$

$A_{4} = \left\{ 1;5 \right\};A_{5} = \left\{ 1;6 \right\};A_{6} = \left\{ 2;3 \right\};$

$A_{7} = \left\{ 2;4 \right\};A_{8} = \left\{ 2;5 \right\};A_{9} = \left\{ 2;6 \right\};$

$A_{10} = \left\{ 3;4 \right\};A_{11} = \left\{ 3;5 \right\};A_{12} = \left\{ 3;6 \right\};$

$A_{13} = \left\{ 4,5 \right\};A_{14} = \left\{ 4;6 \right\};A_{15} = \left\{ 5;6 \right\}.$
Câu 5: Nhận biết
Chọn phương án đúng
Tập hợp nào sau đây có đúng một tập hợp con?
- A.
  $d:y = 2k - 3$ .
- B.
  $\left\{ 1;\ \varnothing \right\}$ .
- C.
  $\left\{ \varnothing \right\}$ .
- D.
  $\varnothing$ .
Hướng dẫn:
Đáp án “ $\varnothing$ ” duy nhất một tập con là $\varnothing$ .

Đáp án “ $d:y = 2k - 3$ ” còn một tập con nữa là tập $\varnothing$ .

Đáp án “ $\left\{ \varnothing \right\}$ ” có hai tập con là $\varnothing$ và $\left\{ \varnothing \right\}$ .

Đáp án “ $\left\{ 1;\ \varnothing \right\}$ ” có ba tập con $\left\{ \varnothing \right\}$ , $\left\{ 1 \right\}$ và $\left\{ 1;\ \varnothing \right\}$ .
Câu 6: Thông hiểu
Chọn cách viết đúng
Cách viết nào sau đây là đúng?
- A.
  $\left\{ a \right\} \in \lbrack a;b\rbrack.$
- B.
  $\left\{ a \right\} \subset \lbrack a;b\rbrack.$
- C.
  $a \subset \lbrack a;b\rbrack.$
- D.
  $a \in (a;b\rbrack.$
Hướng dẫn:
Cách viết đúng là: $\left\{ a \right\} \subset \lbrack a;b\rbrack.$
Câu 7: Thông hiểu
Chọn đáp án đúng
Tập hợp nào sau đây có đúng hai tập hợp con?
- A.
  $\left\{ x;y \right\}$ .
- B.
  $\left\{ x;\varnothing \right\}$ .
- C.
  $\left\{ x \right\}$ .
- D.
  $\left\{ x;y;\varnothing \right\}$ .
Hướng dẫn:
C1: Công thức số tập con của tập hợp có $n$ phần tử là $2^{n}$ nên suy ra tập $\left\{ x \right\}$ có 1 phần tử nên có $2^{1} = 2$ tập con.

C2: Liệt kê số tập con ra thì $\left\{ x \right\}$ có hai tập con là $\left\{ x \right\}$ và $\left\{ \varnothing \right\}$ .
Câu 8: Nhận biết
Tìm mệnh đề sai
Cho tập hợp $P$ . Tìm mệnh đề sai trong các mệnh đề sau?
- A.
  $P \subset P$ .
- B.
  $P \in P$ .
- C.
  $\varnothing \subset P$ .
- D.
  $P \in \left\{ P \right\}$ .
Hướng dẫn:
Các đáp án $P \subset P$ , $\varnothing \subset P$ , $P \in \left\{ P \right\}$ đúng. Đáp án “ $P \in P$ ” sai.
Câu 9: Thông hiểu
Tìm số tập X thỏa mãn điều kiện
Cho tập hợp $A = \left\{ x;y;z \right\}$ và $B = \left\{ x;y;z;t;u \right\}$ . Có bao nhiêu tập $X$ thỏa mãn $A \subset X \subset B$ ?
- A.
  $2$ .
- B.
  $16$ .
- C.
  $8$ .
- D.
  $4$ .
Hướng dẫn:
Có 4 tập hợp $X$ thỏa mãn $A \subset X \subset B$ là:

$X_{1} = \left\{ x;y;z \right\}$ ; $X_{2} = \left\{ x;y;z;t \right\}$ ; $X_{3} = \left\{ x;y;z;u \right\}$ và $X_{4} = \left\{ x;y;z;t;u \right\}$ .
Câu 10: Nhận biết
Chọn câu đúng
Cho tập $X = \left\{ 1;2;3;4 \right\}.$ Câu nào sau đây đúng?
- A.
  Số tập con của $X$ chứa 4 phần tử là $0.$
- B.
  Số tập con của $X$ có hai phần tử là $8.$
- C.
  Số tập con của $X$ là $16.$
- D.
  Số tập con của $X$ chứa số 1 là $6.$
Hướng dẫn:
Số tập con của $X$ là $2^{4} = 16.$
Câu 11: Thông hiểu
Xác định số tập hợp con
Cho $X = \left\{ 2;3;4 \right\}.$ Tập $X$ có bao nhiêu tập hợp con?
- A.
  $3.$
- B.
  $8.$
- C.
  $9.$
- D.
  $6.$
Hướng dẫn:
Các tập hợp con của $X$ là: $\varnothing; \left\{ 2 \right\}; \left\{ 3\right\}; \left\{ 4 \right\};$ $\left\{ 2;3 \right\};\left\{ 3;4\right\}; \left\{ 2;4 \right\}; \left\{ 2;3;4\right\}$ .
Câu 12: Thông hiểu
Xác định số tập con có ba phần tử
Cho tập $X = \left\{ \alpha;\ \ \pi;\ \ \xi;\ \ \psi;\ \ \rho;\ \ \eta;\ \ \gamma;\ \ \sigma;\ \ \omega;\ \ \tau \right\}$ . Số các tập con có ba phần tử trong đó có chứa $\mathbf{\alpha}\mathbf{,}\mathbf{\ }\mathbf{\ }\mathbf{\pi}$ của $X$ là:
- A.
  $10.$
- B.
  $14.$
- C.
  $12.$
- D.
  $8.$
Hướng dẫn:
Tập $X$ có 10 phần từ. Gọi $Y = \left\{ \alpha;\pi;x \right\}$ là tập con của $X$ trong đó $x \in X$ .

Có $8$ cách chọn $x$ từ các phần tử còn lại trong $C$ .

Do đó, có 8 tập con thỏa mãn yêu cầu bài toán.
Câu 13: Nhận biết
Chọn hình vẽ thích hợp
Hình nào sau đây minh họa tập $B$ là con của tập $A$ ?
- A.
- B.
- C.
- D.
Hướng dẫn:
Hình vẽ cần tìm là:
Câu 14: Thông hiểu
Chọn phương án thích hợp
Cho tập hợp $A = \left\{ 1;\ 2;\ a \right\}$ , $B = \left\{ 1;\ 2;\ a;\ b;\ x;\ y \right\}$ . Hỏi có bao nhiêu tập hợp $X$ thỏa $A \subset X \subset B$ ?
- A.
  $2^{n}$ .
- B.
  $6$ .
- C.
  $7$ .
- D.
  $8$ .
Hướng dẫn:
Ta có:

$\left\{ 1;\ 2;\ a \right\},\ \left\{ 1;\ 2;\ a;b \right\}\ ,\ \left\{ 1;\ 2;\ a;x \right\},\ \left\{ 1;\ 2;\ a;\ y \right\},$

$\left\{ 1;\ 2;\ a;b;x \right\},\ \left\{ 1;\ 2;\ a;b;y \right\},\ \left\{ 1;\ 2;\ a;x;y \right\},\left\{ 1;\ 2;\ a;\ b;\ x;\ y \right\}$ .
Câu 15: Thông hiểu
Chọn đáp án đúng
Cho tập hợp $A = \left\{ x;y;z \right\}$ và $B = \left\{ x;y;z;t;u \right\}$ . Có bao nhiêu tập $X$ thỏa mãn $A \subset X \subset B$ ?
- A.
  4.
- B.
  2.
- C.
  16..
- D.
  8.
Hướng dẫn:
Có 4 tập hợp $X$ thỏa mãn $A \subset X \subset B$ là:

$X_{1} = \left\{ x;y;z \right\}$ ; $X_{2} = \left\{ x;y;z;t \right\}$ ; $X_{3} = \left\{ x;y;z;u \right\}$ và $X_{4} = \left\{ x;y;z;t;u \right\}$ .
Câu 16: Thông hiểu
Tìm mệnh đề sai
Cho hai tập hợp $A = \left\{ 1;3;5;7 \right\},B = \left\{ 5;7 \right\}$ . Tìm mệnh đề sai
- A.
  $A \subset B.$
- B.
  $B \subset A.$
- C.
  $B \subset B.$
- D.
  $A \subset A.$
Hướng dẫn:
Định nghĩa tập hợp con

Suy ra đáp án cần chọn là: $\mathbf{A \subset B}\mathbf{.}$
Câu 17: Nhận biết
Tính số tập con của tập X
Cho tập $X = \left\{ 2;3;4;\ \ 5 \right\}.$ Hỏi tập $X$ có bao nhiêu tập hợp con?
- A.
  $16.$
- B.
  $9.$
- C.
  $6.$
- D.
  $8.$
Hướng dẫn:
Số tập con: 2⁴ = 16. (Số tập con của tập có n phần tử là 2ⁿ )
Câu 18: Thông hiểu
Chọn phương án thích hợp
Tập hợp nào sau đây chỉ gồm các số vô tỷ?
- A.
  $\mathbb{R}\backslash\mathbb{Q}$ .
- B.
  $\mathbb{Q}\backslash\mathbb{N}^{*}$ .
- C.
  $\mathbb{R}\backslash\left\{ 0 \right\}$ .
- D.
  $\mathbb{Q}\backslash\mathbb{Z}$ .
Hướng dẫn:
Tập hợp chỉ gồm các số vô tỷ là $\mathbb{R}\backslash\mathbb{Q}$ .
Câu 19: Thông hiểu
Chọn đáp án đúng
Có tất cả bao nhiêu tập $X$ thỏa mãn $\left\{ 1;2 \right\} \subset X \subset \left\{ 1;2;3;4;5 \right\}$ ?
- A.
  $6$ .
- B.
  $1$ .
- C.
  $3$ .
- D.
  $8$ .
Hướng dẫn:
Các $8$ tập $X$ thỏa mãn đề bài là:

$\left\{ 1;2 \right\},\left\{ 1;2;3 \right\},\left\{ 1;2;4 \right\},\left\{ 1;2;5 \right\},\left\{ 1;2;3;4 \right\},$ $\left\{ 1;2;3;5 \right\},\left\{ 1;2;4;5 \right\},\left\{ 1;2;3;4;5 \right\}.$
Câu 20: Nhận biết
Chọn đáp án đúng
Trong các tập hợp sau, tập nào có đúng hai tập hợp con ?
- A.
  $\left\{ x;y \right\}.$
- B.
  $\left\{ \varnothing;x;y \right\}.$
- C.
  $\left\{ x \right\}.$
- D.
  $\left\{ \varnothing;x \right\}.$
Hướng dẫn:
Tập $\left\{ x \right\}$ có hai tập con là $\varnothing;\ \ \left\{ x \right\}.$
Câu 21: Thông hiểu
Chọn đáp án đúng
Tập $A = \left\{ 0;2;4;6 \right\}$ có bao nhiêu tập hợp con có đúng hai phần tử?
- A.
  $6.$
- B.
  $4.$
- C.
  $8.$
- D.
  $7.$
Hướng dẫn:
Các tập con có hai phần tử của tập $A$ là: $A_{1} = \left\{ 0;2 \right\};\ \ A_{2} = \left\{ 0;4 \right\};\ \ A_{3} = \left\{ 0;6 \right\};$ $A_{4} = \left\{ 2;4 \right\};\ \ A_{5} = \left\{ 2;6 \right\};\ \ A_{6} = \left\{ 4;6 \right\}.$
Câu 22: Thông hiểu
Tìm điều kiện cần và đủ
Cho $A = (2; + \infty)$ , $B = (m; + \infty)$ . Điều kiện cần và đủ của $m$ sao cho $B$ là tập con của $A$ là
- A.
  $m \geq 2$ .
- B.
  $m \leq 2$ .
- C.
  $m > 2$ .
- D.
  $m = 2$ .
Hướng dẫn:
Hình vẽ minh họa

Ta có: $B \subset A$ khi và chỉ khi $\forall x \in B \Rightarrow x \in A \Rightarrow m \geq 2$ .
Câu 23: Thông hiểu
Xác định tất cả các tập hợp con của tập B
Cho tập hợp $B = \left\{ x \in \mathbb{N}^{*}| - 3 < x \leq 4 \right\}$ . Tập hợp $B$ có tất cả bao nhiêu tập hợp con?
- A.
  4..
- B.
  16..
- C.
  8.
- D.
  12..
Hướng dẫn:
Ta có: $B = \left\{ x \in \mathbb{N}^{*}| - 3 < x \leq 4 \right\} = \left\{ 1;2;3;4 \right\}$ .

Vậy tập $B$ có $2^{4} = 16$ .
Câu 24: Nhận biết
Xác định số tập con của tập A
Cho $A = \left\{ 1\ ;\ 2\ ;\ 3 \right\}$ , số tập con của $A$ là
- A.
  $5$ .
- B.
  $3$ .
- C.
  $6$ .
- D.
  $8$ .
Hướng dẫn:
Số tập hợp con của tập hợp $A$ là $2^{3} = 8$ .
Câu 25: Thông hiểu
Chọn đáp án đúng
Cho tập hợp $A = \left\{ x\mathbb{\in N}\left| 2x - 3 < \sqrt{7} \right.\ \right\}$ . Tập hợp $A$ có tất cả bao nhiêu tập con khác rỗng.
- A.
  $9.$
- B.
  $7.$
- C.
  $6.$
- D.
  $8.$
Hướng dẫn:
Cách 1: $A = \left\{ x\mathbb{\in N}\left| 2x - 3 < \sqrt{7} \right.\ \right\} = \left\{ 0;1;2 \right\}.$ Liệt kê các tập con của tập $A$ khác rỗng là $\left\{ 0 \right\},\left\{ 1 \right\},\left\{ 2 \right\},\left\{ 0;1 \right\},\left\{ 1,2 \right\},\left\{ 0,2 \right\},\left\{ 0,1,2 \right\}$ do đó chọn B.

Cách 2: Số tất cả các tập con của tập $A$ có $n$ phần tử có công thức $2^{n}.$ Do đó dùng máy tính ấn $2^{3} - 1 = 7$ vì yêu cầu khác tập rỗng.
Câu 26: Nhận biết
Tìm tất cả các tập con của tập A
Cho tập hợp $A = \left\{ a;b;c \right\}$ khi đó tập hợp A có tất cả bao nhiêu tập con.
- A.
  $9$ .
- B.
  $10.$
- C.
  $7$ .
- D.
  $8$ .
Hướng dẫn:
Cách 1: Liệt kê các tập con của tập $A$ là $\varnothing,\left\{ a \right\},\left\{ b \right\},\left\{ c \right\},\left\{ a;b \right\},\left\{ a,c \right\},\left\{ b,c \right\},\left\{ a,b,c \right\}$ do đó chọn đáp án là 8.

Cách 2: Số tất cả các tập con của tập $A$ có $n$ phần tử có công thức $2^{n}.$ Do đó dùng máy tính ấn $2^{3} = 8$
Câu 27: Thông hiểu
Tìm m thỏa mãn điều kiện
Cho tập hợp $B = \left\{ 1;3;m \right\},C = \left\{ x\mathbb{\in R}\left| \left( x^{2} - 4x + 3 \right) = 0 \right.\ \right\}$ . Tìm $\mathbf{m}$ để $C \subset B$
- A.
  $m=0.$
- B.
  $m=3.$
- C.
  $m=4.$
- D.
  $m=1.$
Hướng dẫn:
Giải phương trình $x^{2} - 4x + 3 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 3 \\ \end{matrix} \right.$ mà $x\mathbb{\in R}$ nên $C = \left\{ 1;3 \right\}.$

Để $C \subset B$ thì $m=4.$
Câu 28: Nhận biết
Tìm số tập con theo yêu cầu
Cho tập hợp $A\left\{ 1;2;3;4 \right\}.$ Tập hợp $A$ có tất cả bao nhiêu tập con có đúng 3 phần tử.
- A.
  $16.$
- B.
  $4.$
- C.
  $5.$
- D.
  $3.$
Hướng dẫn:
Cách 1: Liệt kê các tập con của tập $A$ có 3 phần tử là

$\left\{ 1;2;3 \right\},\left\{ 1;2;4 \right\},\left\{ 1;3;4 \right\},\left\{ 2;3;4 \right\}$ do đó chọn đáp án 4.

Cách 2: Cho tập A có $n$ phần tử, số tập con của tập $A$ có $k$ phần tử có công thức $C_{n}^{k}.$ Do đó dùng máy tính ấn $C_{4}^{3} = 4$

Chia sẻ bởi:
Bon

1

37

Xác thực tài khoản!

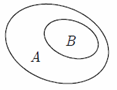
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Chuyên đề Toán 10

Xem thêm

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Bài tập Toán 10 Tập hợp con có đáp án chi tiết

Bài tập Toán 10: Tập hợp - Tập hợp con (Có đáp án chi tiết)

Chúc mừng Bạn đã hoàn thành bài!

A. CHUYÊN ĐỀ TỰ LUẬN

B. CHUYÊN ĐỀ TRẮC NGHIỆM

Lớp 10

Toán lớp 10

Chuyên đề Toán 10

Chuyên đề Toán 10

Xác định Parabol y = ax^2 + bx + c

Viết phương trình tham số, phương trình chính tắc của đường thẳng

Xác định vectơ chỉ phương của đường thẳng

Phương trình tổng quát của đường thẳng

Bài tập tích vô hướng của hai vectơ

Tìm m để đường thẳng cắt Parabol tại hai điểm phân biệt