Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 10 Toán lớp 10 Chuyên đề Toán 10

Phương trình chứa ẩn trong dấu giá trị tuyệt đối

Chuyên đề môn Toán lớp 10
Lớp: Lớp 10
Môn: Toán
Dạng tài liệu: Chuyên đề
Phân loại: Tài liệu Tính phí

Chuyên đề Toán học lớp 10: Phương trình chứa ẩn trong dấu giá trị tuyệt đối được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo!

Chuyên đề: Phương trình chứa ẩn trong dấu giá trị tuyệt đối

I. Cách giải phương trình chứa dấu giá trị tuyệt đối

Để giải phương trình chứa ẩn trong dấu giá trị tuyệt đối (GTTĐ) ta tìm cách để khử dấu giá trị tuyệt đối, bằng cách:

  • Dùng định nghĩa hoặc tính chất của GTTĐ.
  • Bình phương hai vế.
  • Đặt ẩn phụ.

Phương trình dạng |f(x)|=|g(x)| ta có thể giải bằng cách biến đổi tương đương như sau:

|f(x)| = |g(x)| ⇔ f(x) = g(x) hoặc f(x) = -g(x)

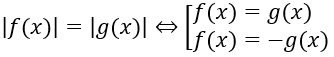
hoặc |f(x)| = |g(x)|⇔ f2(x) = g2(x)

- Đối với phương trình dạng |f(x)| = g(x)(*) ta có thể biến đổi tương đương như sau:

|f(x) = g(x) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {g\left( x \right) \geqslant 0} \\ {{f^2}\left( x \right) = {g^2}\left( x \right)} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {g\left( x \right) \geqslant 0} \\ {\left[ \begin{gathered} f\left( x \right) = g\left( x \right) \hfill \\ f\left( x \right) = - g\left( x \right) \hfill \\ \end{gathered} \right.} \end{array}} \right.

Hoặc |f(x) = g(x)\Leftrightarrow \left[ \begin{gathered} \left\{ {\begin{array}{*{20}{c}} {f\left( x \right) \geqslant 0} \\ {f\left( x \right) = g\left( x \right)} \end{array}} \right. \hfill \\ \left\{ {\begin{array}{*{20}{c}} {f\left( x \right) < 0} \\ { - f\left( x \right) = g\left( x \right)} \end{array}} \right. \hfill \\ \end{gathered} \right..

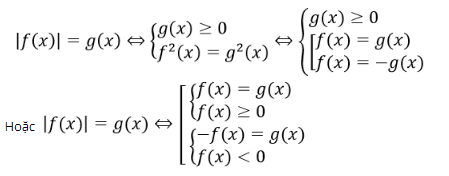
Nếu f(x) = ax2 + bx + c = (Ax ± B)2 tức là có dạng hằng đẳng thức thì: KHAI CĂN.

Phương trình |Ax \pm B| = e \Leftrightarrow \left\lbrack \begin{matrix} Ax \pm B = \ \ \ \ \ e \\ Ax \pm B = - e \\ \end{matrix} \right. => Tìm giá trị của x.

Ví dụ: Giải các phương trình sau: \sqrt{x^{2} - 4x + 4} = 3.

Lời giải chi tiết:

Vì x2 – 4x + 4 = (x – 2)2, ta có:

Phương trình: \sqrt{(x - 2)^{2}} = 3 tương đương:

|x - 2| = 3 \Leftrightarrow \left\lbrack \begin{matrix} x - 2 = \ \ \ \ \ 3 \\ x - 2 = - 3 \\ \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} x = \ \ \ \ \ 5 \\ x = - 1 \\ \end{matrix} \right.

Vậy phương trình có nghiêm x = 5 hoặc x = -1.

Nếu f(x) = ax2 + bx + c không có dạng hằng đẳng thức thì: BÌNH PHƯƠNG 2 VẾ.

Bước 1: Viết điều kiện f(x) ≥ 0.

Bước 2: Bình phương 2 vế phương trình (để làm mất căn).

Bước 3: Giải phương trình bậc hai có được bằng cách: Phân tích thành nhân tử, đưa về phương trình tích.

Ví dụ : Giải phương trình sau: \sqrt{x^{2} - 4x - 6} = \sqrt{15}.

Lời giải chi tiết:

Nhận xét: x2 – 4x – 6 không có dạng (Ax ± B)2 nên ta không đưa được về phương trình trị tuyệt đối

Điều kiện: x2 – 4x – 6 ≥ 0

Bình phương hai vế phương trình ta được:

x2 – 4x – 6 = 15

⇔ x2 – 4x – 21 = 0

⇔ (x – 7) (x + 3) = 0

⇔ x = 7 hoặc x = - 3

Thay x tìm được vào điều kiện ta thấy cả x = 7 và x = - 3 đều thỏa mãn

Vậy phương trình có nghiệm x = 7 ; x = - 3.

Phương trình có dạng \sqrt{\left\lbrack f(x) \right\rbrack^{2}} \pm \sqrt{\left\lbrack h(x) \right\rbrack^{2}} = g(x) ta làm như sau:

Bước 1: Nếu bản thân f(x) và g(x) có chứa căn bậc hai thì có điều kiện trong căn.

Bước 2: Đưa phương trình về dạng phương trình trị tuyệt đối.

|f(x)| ± |h(x)| = g(x)

Bước 3: Xét dấu trị tuyệt đối và giải phương trình.

Ví dụ: Giải phương trình \sqrt{x + 4 - 4\sqrt{x}} - \sqrt{x + 9 - 6\sqrt{x}} = 1.

Lời giải chi tiết:

Điều kiện xác định: x ≥ 0

Với phương trình này ta dễ dàng nhận thấy:

x + 4 - 4\sqrt{x} = \left( \sqrt{x} - 2 \right)^{2}

⇔ x + 9 - 6\sqrt{x} = \left( \sqrt{x} - 3 \right)^{2}

Phương trình \left| \sqrt{x} - 2 \right| - \left| \sqrt{x} - 3 \right| = 1

Trường hợp 1: Nếu \left\{ \begin{matrix} \sqrt{x} - 2 \geq 0 \\ \sqrt{x} - 3 \geq 0 \\ \end{matrix} \right.\ \Leftrightarrow \sqrt{x} \geq 3 \Leftrightarrow x \geq 9 ta có:

0.\sqrt{x} = 0 => Phương trình có vô số nghiệm x ≥ 0

Trường hợp 2. Nếu \left\{ \begin{matrix} \sqrt{x} - 2 \geq 0 \\ \sqrt{x} - 3 < 0 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \geq 4 \\ x < 9 \\ \end{matrix} \right. ta có

\left( \sqrt{x} - 2 \right) - \left( 3 - \sqrt{x} \right) = 1 \Leftrightarrow 2\sqrt{x} = 6 \Leftrightarrow x = 9 (Loại)

Trường hợp 3. Nếu \left\{ \begin{matrix} \sqrt{x} - 2 < 0 \\ \sqrt{x} - 3 \geq 0 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x < 4 \\ x \geq 9 \\ \end{matrix} \right.\ \Leftrightarrow x \in \varnothing

Trường hợp 4. Nếu \left\{ \begin{matrix} \sqrt{x} - 2 < 0 \\ \sqrt{x} - 3 < 0 \\ \end{matrix} \right.\ \Leftrightarrow \sqrt{x} < 2 \Leftrightarrow x < 4 ta có:

\left( 2 - \sqrt{x} \right) - \left( 3 - \sqrt{x} \right) = 1 \Leftrightarrow 0.\sqrt{x} = 2 => Phương trình có vô nghiệm

Kết luận: Vậy phương trình có vô số nghiệm x ≥ 0.

II. Bài tập giải phương trình giá trị tuyệt đối

Bài 1: Giải phương trình |3x - 2| = x2 + 2x + 3.

Lời giải chi tiết

Ta có:

|3x - 2| bằng 3x - 2 khi x ≥ 2/3 hoặc -3x + 2 khi x < 2/3.

* Nếu x ≥ 2/3 ⇒ Phương trình ⇔ 3x - 2 = x2 + 2x + 3 ⇔ x2 - x + 5 = 0 phương trình vô nghiệm

* Nếu x < 2/3 ⇒ Phương trình ⇔ -3x + 2 = x2 + 2x + 3 ⇔ x2 + 5x + 1 = 0

⇔ x = (-5 ± √21)/2 hai nghiệm này đều thỏa mãn x < 2/3

Vậy nghiệm của phương trình đã cho là x = (-5 ± √21)/2.

Bài 2: Giải phương trình |x3 - 1| = |x2 - 3x + 2|.

Lời giải chi tiết

Hai vế không âm bình phương hai vế ta có:

(x3 - 1)2 = (x2 - 3x + 2)2

⇔ (x3 - 1)2 - (x2 - 3x + 2)2 = 0

⇔ (x3 - 1 - x2 + 3x - 2).(x3 - 1 + x2 - 3x + 2) = 0

⇔ (x3 - x2 + 3x - 3).(x3 + x2 - 3x + 1) = 0

⇔ \left[ \begin{gathered} x = 1 \hfill \\ x = - 1 + \sqrt 2 \hfill \\ x = - 1 - \sqrt 2 \hfill \\ \end{gathered} \right.

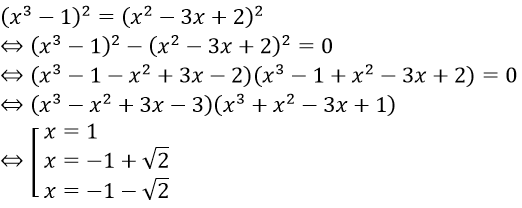
Vậy tập nghiệm của phương trình đã cho là S = {1; -1 + √2; -1 - √2}.

Bài 3: Giải phương trình{x^2} + \frac{9}{{{{\left( {x - 1} \right)}^2}}} + 1 = 2x + 7 + 7.\left| {\frac{{{x^2} - 2x - 2}}{{x - 1}}} \right|.

Lời giải chi tiết

ĐKXĐ: x ≠ 1

Phương trình tương đương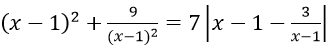 {\left( {x - 1} \right)^2} + \frac{9}{{{{\left( {x - 1} \right)}^2}}} = 7.\left| {x - 1 - \frac{3}{{x - 1}}} \right|

Đặt t = |x - 1 - 3/(x-1)|

Suy ra: {t^2} = {\left( {x - 1} \right)^2} + \frac{9}{{{{\left( {x - 1} \right)}^2}}} - 6\Rightarrow {\left( {x - 1} \right)^2} + \frac{9}{{{{\left( {x - 1} \right)}^2}}} = {t^2} + 6

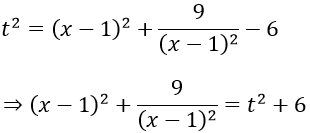
Phương trình trở thành t2 + 6 = 7t ⇔ t2 - 7t + 6 = 0 ⇔ 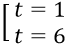t = 1 hoặc t = 6.

Với t = 1 ta có:

\left| {x - 1 - \frac{3}{{x - 1}}} \right| = 1 \Leftrightarrow \left| {\frac{{{x^2} - 2x - 2}}{{x - 1}}} \right| = 1

\Leftrightarrow \frac{{{x^2} - 2x - 2}}{{x - 1}} = \pm 1 \Leftrightarrow \left[ \begin{gathered} {x^2} - 3x - 1 = 0 \hfill \\ {x^2} - x - 3 = 0 \hfill \\ \end{gathered} \right.

\Leftrightarrow \left[ \begin{gathered} x = \frac{{3 \pm \sqrt {13} }}{2} \hfill \\ x = \frac{{1 \pm \sqrt {13} }}{2} \hfill \\ \end{gathered} \right.

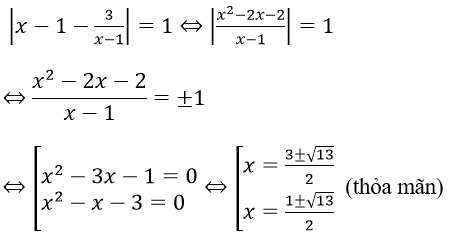
Với t = 6 ta có

\Leftrightarrow \left| {x - 1 - \frac{3}{{x - 1}}} \right| = 6 \Leftrightarrow \left| {\frac{{{x^2} - 2x - 2}}{{x - 1}}} \right| = 6

\Leftrightarrow \frac{{{x^2} - 2x - 2}}{{x - 1}} = \pm 6 \Leftrightarrow \left[ \begin{gathered} {x^2} - 8x + 4 = 0 \hfill \\ {x^2} + 4x - 8 = 0 \hfill \\ \end{gathered} \right.\Leftrightarrow \left[ \begin{gathered} x = 4 \pm 2\sqrt 3 \hfill \\ x = - 2 \pm 2\sqrt 3 \hfill \\ \end{gathered} \right.

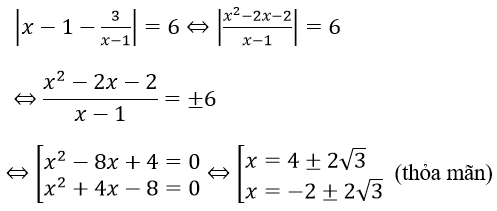
Vậy phương trình có nghiệm là: x\frac{{3 \pm \sqrt {13} }}{2};x = \frac{{1 \pm \sqrt {13} }}{2}; {x = 4 \pm 2\sqrt 3 ;x = - 2 \pm 2\sqrt 3 }

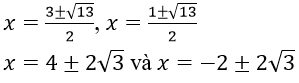
Bài 4: Giải phương trình |2x - 5| + |2x2 - 7x + 5| = 0.

Lời giải chi tiết:

Ta có:

\left\{ \begin{gathered} \left| {2x - 5} \right| \geqslant 0 \hfill \\ \left| {2{x^2} - 7x + 5} \right| \geqslant 0 \hfill \\ \end{gathered} \right.

=> |2x - 5| + |2x2 - 7x + 5| ≥ 0

Dấu "=" xảy ra khi và chỉ khi: 2x - 5 = 0 và 2x2 - 7x + 5 = 0 hay x = 5/2

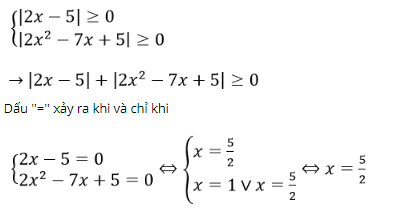
Vậy tập nghiệm của phương trình là S = {5/2}

Bài 5: Phương trình (x+1)2 - 3|x+1| + 2 = 0 có bao nhiêu nghiệm?

Lời giải chi tiết

Đặt t = |x + 1|, t ≥ 0

Phương trình trở thành t2 - 3t + 2 = 0 ⇔ 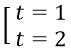t = 1 hoặc t = 2

Với t = 1 ta có |x + 1| = 1 ⇔ x + 1 = ±1 ⇔ 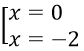x = 0 hoặc x = -2.

Với t = 2 ta có |x + 1| = 2 ⇔ x + 1 = ±2 ⇔ x = 1 hoặc x = -3.

Vậy phương trình có nghiệm là x = -3, x = -2, x = 0 và x = 1.

--------------------------------------------------------

Với nội dung bài Phương trình chứa ẩn trong dấu giá trị tuyệt đối trên đây chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững khái niệm, phương pháp giải phương trình có chứa ẩn trong dấu giá trị tuyệt đối....

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Phương trình chứa ẩn trong dấu giá trị tuyệt đối. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!
Đóng
79.000 / tháng
Mua ngay
Đặc quyền các gói Thành viên
PRO
Phổ biến nhất
PRO+
Tải tài liệu Cao cấp 1 Lớp
30 lượt tải tài liệu
Xem nội dung bài viết
Trải nghiệm Không quảng cáo
Làm bài trắc nghiệm không giới hạn
Mua cả năm Tiết kiệm tới 48%
5
17.440 Bài viết đã được lưu
Mục lục

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này