Cho hai tập hợp và
Có bao nhiêu tập hợp
thỏa mãn
Vì nên
chắc chắn có chứa các phần tử
Các tập có thể là
Tìm hợp của các tập hợp là một trong những dạng bài toán cơ bản nhưng quan trọng trong chương trình Toán lớp 10. Việc hiểu rõ cách xác định hợp giữa hai hay nhiều tập hợp sẽ giúp học sinh làm tốt các bài kiểm tra và vận dụng linh hoạt trong các bài toán liên quan đến tập hợp, mệnh đề và logic. Trong bài viết này, bạn sẽ được luyện tập với nhiều dạng bài tập tìm hợp các tập hợp kèm theo đáp án chi tiết và hướng dẫn giải dễ hiểu, giúp bạn nắm vững kiến thức và cải thiện kỹ năng làm bài.
Cho hai tập hợp và
Có bao nhiêu tập hợp
thỏa mãn
Vì nên
chắc chắn có chứa các phần tử
Các tập có thể là
Cho hai tập hợp . Xác định tập hợp
Ta có:
Cho các tập hợp khác rỗng và
. Tập hợp các giá trị thực của
để
là
Để thì điều kiện là
.
Vậy .
Cho ,
,
. Chọn phát biểu sai.
Ta có:
Vậy câu sai là:
Cho tập hợp . Mệnh đề nào sau đây sai?
Ta có .
Cho ,
,
. Tập
có bao nhiêu phần tử là số nguyên.
Ta có : có
phần tử là số nguyên.
Cho ba tập hợp: ,
,
. Chọn câu đúng nhất:
Ta có:
;
.
sai.
sai.
sai.
.
Vậy là đáp án đúng nhất.
Gọi là tập hợp các bội số của
trong
. Xác định tập hợp
Ta có các tập hợp
.
Cho hai tập hợp khi đó:
Cách 1: Giải phương trình . Mà
nên
Giải bất phương trình . mà
nên chọn
Giải bất phương trình
Cách 2: Ta thử từng phần tử của các đáp án, nếu thỏa yêu cầu bài toán của cả tập hoặc
thì đó là đáp án đúng.
Cho ;
. Điều kiện để
là
Ta có: .
Kết quả của là
Cách 1: Gọi , ta có:
Chọn
.
Cách 2: Biểu diễn hai tập hợp và
trên trục số rồi tìm hợp của hai tập hợp.
Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?

Đáp án cần tìm là:
Cho ba tập hợp
khi đó tập
là:
Giải phương trình mà
nên
Giải bất phương trình . Mà
nên chọn
Giải phương trình mà
nên
Giải bất phương trình
Cho ,
,
. Câu nào sau đây đúng?
Đáp án đúng là: “”.
Cho hai tập hợp khi đó tập
là
Ta tìm tất cả các phần tử của cả hai tập hợp.
Thu được kết quả
Cho tập hợp D = , E = [-3; 1]. Khi đó
là:
Ta có D =
Biểu diễn hai tập hợp D và E trên trục số ta được:
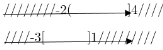
= [-3;4]
Cho hai tập hợp và
. Tập hợp
có bao nhiêu phần tử?
Ta có . Do đó
có
phần tử.
Cho hai tập hợp
khi đó tập
là:
Cách 1: Giải phương trình .
Mà nên
Giải bất phương trình . mà
nên chọn
Giải bất phương trình
Cách 2: Ta thử từng phần tử của các đáp án, nếu thỏa yêu cầu bài toán của cả tập hoặc
thì đó là đáp án đúng.
Cho ,
,
Khi đó tập
là
Ta có . Suy ra
.
Cho hai tập hợp và
. Tìm
.
Thực hiện phép hợp trên hai tập hợp và
ta được:
.
Cho các tập hợp ,
,
. Khẳng định nào sau đây đúng?
Xét đáp án ta có:
.
Xét đáp án ta có:
Cho ;
;
. Khi đó
là:
Biểu diễn các tập số trên trục số ta được kết quả:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: