Giải và biện luận phương trình bậc hai

Chuyên đề Toán học lớp 10: Giải và biện luận phương trình bậc hai được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo.

I. Lý thuyết & Phương pháp giải

Giải và biện luận phương trình bậc hai ax² + bx + c = 0

Bước 1. Biến đổi phương trình về đúng dạng ax² + bx + c = 0

Bước 2. Nếu hệ số a chứa tham số, ta xét 2 trường hợp:

- Trường hợp 1: a = 0, ta giải và biện luận ax + b = 0.

- Trường hợp 2: a ≠ 0. Ta lập Δ = b² - 4ac. Khi đó:

+ Nếu Δ > 0 thì phương trình có 2 nghiệm phân biệt

+ Nếu Δ = 0 thì phương trình có 1 nghiệm (kép): x = -b/2a

+ Nếu Δ < 0 thì phương trình vô nghiệm.

Bước 3. Kết luận.

Lưu ý:

- Phương trình ax² + bx + c = 0 có nghiệm

- Phương trình ax² + bx + c = 0 có nghiệm duy nhất

II. Ví dụ minh họa

Bài 1: Phương trình (m–1)x² + 3x – 1 = 0. Phương trình có nghiệm khi:

Hướng dẫn:

Với m = 1, phương trình trở thành 3x - 1 = 0 ⇔ x = 1/3

Do đó m = 1 thỏa mãn.

Với m ≠ 1, ta có Δ = 9 + 4(m-1) = 4m + 5

Phương trình có nghiệm khi Δ ≥ 0

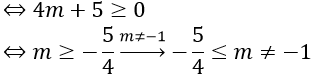
Hợp hai trường hợp ta được m ≥ -5/4 là giá trị cần tìm

Bài 2: Phương trình (x² - 3x + m)(x - 1) = 0 có 3 nghiệm phân biệt khi:

Hướng dẫn:

Phương trình (x² - 3x + m)(x - 1) = 0 ⇔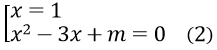

Phương trình (1) có 3 nghiệm phân biệt

⇔ Phương trình (2) có hai nghiệm phân biệt khác 1

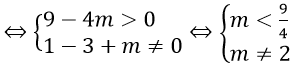
Bài 3: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 10] để phương trình mx² - mx + 1 = 0 có nghiệm.

Hướng dẫn:

Nếu m = 0 thì phương trình trở thành 1 = 0: vô nghiệm.

Khi m ≠ 0, phương trình đã cho có nghiệm khi và chỉ khi

Δ = m² - 4m ≥ 0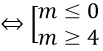

Kết hợp điều kiện m ≠ 0, ta được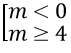

Vì ∈ Z, m ∈ [-10;10] m ∈ {-10; -9; -8;...; -1} ∪ {4; 5; 6;...; 10}

Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán

Bài 4: Tìm tất cả các giá trị thực của tham số m để hai đồ thị hàm số y = -x² - 2x + 3 và y = x² - m có điểm chung

Hướng dẫn:

Phương trình hoành độ giao điểm -x² - 2x + 3 = x² - m

⇔ 2x² + 2x - m - 3 = 0. (*)

Để hai đồ thị hàm số có điểm chung khi và chỉ khi phương trình (*) có nghiệm

⇔ Δ' = 1 - 2(-m-3) ≥ 0 ⇔ m ≥ -7/2

Bài 5: Tìm giá trị thực của tham số m để đường thẳng d: y = 2x + m tiếp xúc với parabol (P): y = (m–1)x² + 2mx + 3m – 1

Hướng dẫn:

Phương trình hoành độ giao điểm (m-1)x² + 2mx + 3m - 1 = 2x + m

⇔ (m-1)x² + 2(m-1)x + 2m - 1 = 0 (*)

Để d tiếp xúc với (P) khi và chỉ khi phương trình (*) có nghiệm kép

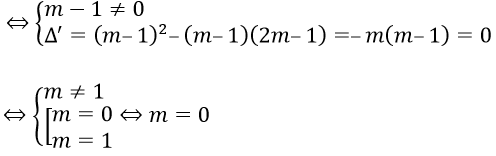
Với nội dung bài Giải và biện luận phương trình bậc hai chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững phương pháp giải và biện luận cách giải phương trình bậc hai....

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Giải và biện luận phương trình bậc hai. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc