VnDoc.com

Tập nghiệm của bất phương trình

Tìm tập nghiệm của bất phương trình lớp 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bất phương trình Toán 10

1. Tập nghiệm S của bất phương trình là gì?
2. Bài tập ví dụ minh họa
3. Bài tập tự rèn luyện

Trong chương trình Toán lớp 10, chuyên đề Tập nghiệm của bất phương trình là một trong những nội dung nền tảng và có mặt xuyên suốt trong các bài kiểm tra, bài tập tự luận, trắc nghiệm lẫn đề thi học kỳ. Việc xác định tập nghiệm không chỉ giúp học sinh nắm chắc bản chất của bất phương trình mà còn là kỹ năng quan trọng để làm tốt các chuyên đề nâng cao sau này như: bất phương trình chứa căn, chứa trị tuyệt đối, hệ bất phương trình hay bất phương trình bậc hai.

Bài viết này được xây dựng nhằm giúp bạn:

Hiểu rõ khái niệm tập nghiệm và ý nghĩa của nó trong giải toán;
Nắm trọn các phương pháp giải bất phương trình lớp 10 từ cơ bản đến nâng cao;
Phân biệt chính xác các dạng bất phương trình thường gặp;
Rèn luyện kỹ năng tìm tập nghiệm qua ví dụ minh họa – bài tập tự luyện – đáp án chi tiết;
Tăng tốc độ làm bài, hạn chế sai lầm khi biểu diễn nghiệm trên trục số.

Nếu bạn đang học Toán 10, chuẩn bị kiểm tra định kỳ, hoặc đang tìm tài liệu chuẩn để “nằm lòng” dạng toán này, bài viết sẽ là trợ thủ đáng tin cậy giúp bạn học nhanh – hiểu sâu – vận dụng linh hoạt.

Tài liệu do VnDoc.com biên soạn và đăng tải, nghiêm cấm các hành vi sao chép với mục đích thương mại.

Tìm tập nghiệm của bất phương trình

1. Bất phương trình

Trước hết ta xét đến định nghĩa bất phương trình một ẩn

Định nghĩa:

Bất phương trình một ẩn là một mệnh đề chứa biến x so sánh hai hàm số f(x) và g(x) trên trường số thực dưới một trong các dạng

$f(x) < g(x), f(x) > g(x); f(x) ≥ g(x); f(x) ≤ g(x)$

Giao của hai tập xác định của các hàm số f(x) và g(x) được gọi là tập xác định của bất phương trình.
Nếu với giá trị x =a, f(a) > 0 là bất đẳng thức đúng thì ta nói rằng a nghiệm đúng bất phương trình f(x) > 0, hay a là nghiệm của bất phương trình.

Tập nghiệm S của bất phương trình

- Tập hợp tất cả các nghiệm của bất phương trình được gọi là tập nghiệm hay lời giải của bất phương trình, đôi khi nó cũng được gọi là miền đúng của bất phương trình.

Trong nhiều tài liệu người ta cũng gọi tập nghiệm của bất phương trình là nghiệm của bất phương trình.

Ví dụ Bất phương trình 4.x + 2 > 0 nghiệm đúng với mọi số thực x > -0.5. Tập nghiệm của bất phương trình là { x ∈ R | x > -0.5 } = (0.5; $\infty$ $\infty$)

Phân loại bất phương trình:

Các bất phương trình đại số bậc k là các bất phương trình trong đó f(x) là đa thức bậc k.
Các bất phương trình vô tỷ là các bất phương trình có chứa phép khai căn
Các bất phương trình mũ là các bất phương trình có chứa hàm mũ (chứa biến trên lũy thừa.
Các bất phương trình logarit là các bất phương trình có chứa hàm logarit (chứa biến trong dấu logarit).

2. Cách xét dấu tam thức bậc hai

Xét tam thức bậc hai $y = ax^{2} + bx + c;(a \neq 0)$ $y = ax^{2} + bx + c;(a \neq 0)$

$y \geq 0\left( \forall x\mathbb{\in R} \right) \Leftrightarrow \left\{ \begin{matrix} a > 0 \\ \Delta \leq 0 \\ \end{matrix} \right.$ $y \geq 0\left( \forall x\mathbb{\in R} \right) \Leftrightarrow \left\{ \begin{matrix} a > 0 \\ \Delta \leq 0 \\ \end{matrix} \right.$

$y \leq 0;\left( \forall x\mathbb{\in R} \right) \Leftrightarrow \left\{ \begin{matrix} a < 0 \\ \Delta \leq 0 \\ \end{matrix} \right.$ $y \leq 0;\left( \forall x\mathbb{\in R} \right) \Leftrightarrow \left\{ \begin{matrix} a < 0 \\ \Delta \leq 0 \\ \end{matrix} \right.$

3. Cách giải bất phương trình

Các dạng bất phương trình chứa căn

Dạng 1: Bất phương trình có dạng: $\sqrt{f(x)} < g(x) \Leftrightarrow \left\{ \begin{matrix} g(x) > 0 \\ 0 \leq f(x) < g^{2}(x) \\ \end{matrix} \right.$ $\sqrt{f(x)} < g(x) \Leftrightarrow \left\{ \begin{matrix} g(x) > 0 \\ 0 \leq f(x) < g^{2}(x) \\ \end{matrix} \right.$

Dạng 2: Bất phương trình: $\sqrt{f(x)} > g(x) \Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} g(x) < 0 \\ f(x) \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} g(x) \geq 0 \\ f(x) > g^{2}(x) \\ \end{matrix} \right.\ \\ \end{matrix} \right.$ $\sqrt{f(x)} > g(x) \Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} g(x) < 0 \\ f(x) \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} g(x) \geq 0 \\ f(x) > g^{2}(x) \\ \end{matrix} \right.\ \\ \end{matrix} \right.$

Cách giải bất phương trình chứa căn

Khi giải bất phương trình ta sẽ làm theo các bước cơ bản sau:

Bước 1: Tìm điều kiện xác định (nếu có)

Bước 2: Sử dụng phép biến đổi tương đương chuyển bất phương trình về hệ bất phương trình đại số, từ đó xác định nghiệm x

Bước 3: kiểm tra nghiệm cùng điều kiện ở bước 1

Bước 4. Kết luận

2. Bài toán giải bất phương trình lớp 10

Bài tập 1: Tìm tập nghiệm S của bất phương trình $\sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15$ $\sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15$

Hướng dẫn giải

Điều kiện xác định: ${x^2} - 5x - 6 \geqslant 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right] \cup \left[ {6; + \infty } \right)$ ${x^2} - 5x - 6 \geqslant 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right] \cup \left[ {6; + \infty } \right)$

Bất phương trình tương đương:
$\begin{matrix} \sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15 \hfill \\ \Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2{x^2} + 10x + 15 \hfill \\ \Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2\left( {{x^2} - 5x - 6} \right) + 3\left( * \right) \hfill \\ \end{matrix}$ $\begin{matrix} \sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15 \hfill \\ \Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2{x^2} + 10x + 15 \hfill \\ \Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2\left( {{x^2} - 5x - 6} \right) + 3\left( * \right) \hfill \\ \end{matrix}$
Đặt $\sqrt {{x^2} - 5x - 6} = t;\left( {t \geqslant 0} \right)$ $\sqrt {{x^2} - 5x - 6} = t;\left( {t \geqslant 0} \right)$ (**)

$\begin{matrix} \left( * \right) \Leftrightarrow t > - 2{t^2} + 3 \hfill \\ \Leftrightarrow 2{t^2} + t - 3 > 0 \hfill \\ \Leftrightarrow t \in \left( { - \infty ; - \dfrac{3}{2}} \right] \cup \left[ {1; + \infty } \right) \hfill \\ \end{matrix}$ $\begin{matrix} \left( * \right) \Leftrightarrow t > - 2{t^2} + 3 \hfill \\ \Leftrightarrow 2{t^2} + t - 3 > 0 \hfill \\ \Leftrightarrow t \in \left( { - \infty ; - \dfrac{3}{2}} \right] \cup \left[ {1; + \infty } \right) \hfill \\ \end{matrix}$

Kết hợp với điều kiện (**) $\Rightarrow t \in \left[ {1; + \infty } \right)$ $\Rightarrow t \in \left[ {1; + \infty } \right)$

$\begin{matrix} \Rightarrow \sqrt {{x^2} - 5x - 6} \geqslant 1 \Leftrightarrow {x^2} - 5x - 6 \geqslant 1 \hfill \\ \Rightarrow x \in \left( { - \infty ;\dfrac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\dfrac{{5 + \sqrt {53} }}{2}; + \infty } \right) \hfill \\ \end{matrix}$ $\begin{matrix} \Rightarrow \sqrt {{x^2} - 5x - 6} \geqslant 1 \Leftrightarrow {x^2} - 5x - 6 \geqslant 1 \hfill \\ \Rightarrow x \in \left( { - \infty ;\dfrac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\dfrac{{5 + \sqrt {53} }}{2}; + \infty } \right) \hfill \\ \end{matrix}$

Vậy tập nghiệm của bất phương trình là $x \in \left( { - \infty ;\frac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\frac{{5 + \sqrt {53} }}{2}; + \infty } \right)$ $x \in \left( { - \infty ;\frac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\frac{{5 + \sqrt {53} }}{2}; + \infty } \right)$

Bài tập 2: Tìm tập nghiệm của bất phương trình: $\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0$ $\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0$

Hướng dẫn giải

Điều kiện xác định x² – 6x + 8 ≠ 0 ⟺ x ≠ 2, x ≠ 4

$\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0 \Leftrightarrow \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x - 4} \right)\left( {x - 2} \right)}} \leqslant 0 \Leftrightarrow \frac{{x + 2}}{{x - 4}} \leqslant 0$ $\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0 \Leftrightarrow \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x - 4} \right)\left( {x - 2} \right)}} \leqslant 0 \Leftrightarrow \frac{{x + 2}}{{x - 4}} \leqslant 0$

Lập bảng xét dấu ta có:

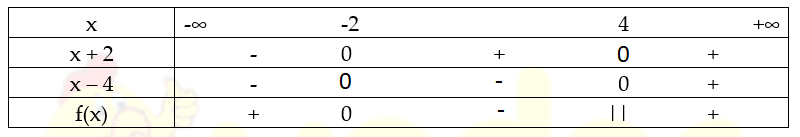
Tập nghiệm của bất phương trình

Từ bảng xét dấu ta kết luận: Tập nghiệm của bất phương trình là: x ∈ [ -2 ; 4)

Bài tập 3: Giải bất phương trình: (x² + 3x + 1)(x² + 3x – 3) ≥ 5 (*)

Hướng dẫn giải

Tập xác định D = $\mathbb{R}$ $\mathbb{R}$

Đặt x² + 3x – 3 = t ⟹ x² + 3x + 1 = t + 4

Bất phương trình (*) ⟺ t(t+4) ≥ 5

⟺ t² + 4t – 5 ≥ 0

⟺ t ∈ (-∞; -5] ∪ [1; +∞)

$\begin{matrix} \Rightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} + 3x - 3 \leqslant - 5} \\ {{x^2} + 3x - 3 \geqslant 1} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} + 3x + 2 \leqslant 0} \\ {{x^2} + 3x - 4 \geqslant 0} \end{array}} \right. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x \in \left[ { - 2; - 1} \right]} \\ {x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right)} \end{array}} \right. \Rightarrow x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right) \hfill \\ \end{matrix}$ $\begin{matrix} \Rightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} + 3x - 3 \leqslant - 5} \\ {{x^2} + 3x - 3 \geqslant 1} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} + 3x + 2 \leqslant 0} \\ {{x^2} + 3x - 4 \geqslant 0} \end{array}} \right. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x \in \left[ { - 2; - 1} \right]} \\ {x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right)} \end{array}} \right. \Rightarrow x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right) \hfill \\ \end{matrix}$

Vậy tập nghiệm của bất phương trình là x ∈ (-∞; -4] ∪ [1; +∞)

Bài tập 4: Giải bất phương trình: $\sqrt{5x + 1} - \sqrt{4x - 1} \leq 3\sqrt{x}$ $\sqrt{5x + 1} - \sqrt{4x - 1} \leq 3\sqrt{x}$

Hướng dẫn giải

Điều kiện xác định: $\left\{ \begin{matrix} 5x + 1 \geq 0 \\ 4x - 1 \geq 0 \\ x \geq 0 \\ \end{matrix} \right.$ $\left\{ \begin{matrix} 5x + 1 \geq 0 \\ 4x - 1 \geq 0 \\ x \geq 0 \\ \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} x \geq \dfrac{- 1}{5} \\ x \geq \dfrac{1}{4} \\ x \geq 0 \\ \end{matrix} \right.\ \Leftrightarrow x \geq \frac{1}{4}$ $\Leftrightarrow \left\{ \begin{matrix} x \geq \dfrac{- 1}{5} \\ x \geq \dfrac{1}{4} \\ x \geq 0 \\ \end{matrix} \right.\ \Leftrightarrow x \geq \frac{1}{4}$

Bất phương trình tương đương: $\sqrt{5x + 1} \leq 3\sqrt{x} + \sqrt{4x - 1}$ $\sqrt{5x + 1} \leq 3\sqrt{x} + \sqrt{4x - 1}$

$\Leftrightarrow 5x + 1 \leq 9x + 4x - 1 + 6\sqrt{x(4x - 1)}$ $\Leftrightarrow 5x + 1 \leq 9x + 4x - 1 + 6\sqrt{x(4x - 1)}$

$\Leftrightarrow 3\sqrt{x(4x - 1)} \geq 1 - 4x$ $\Leftrightarrow 3\sqrt{x(4x - 1)} \geq 1 - 4x$ luôn đúng với điều kiện đề bài

Vậy bất phương trình có tập nghiệm $x \geq \frac{1}{4}$ $x \geq \frac{1}{4}$

Bài tập 5: Giải bất phương trình: $\frac{1 - \sqrt{1 - 4x^{2}}}{x} < 3$ $\frac{1 - \sqrt{1 - 4x^{2}}}{x} < 3$

Hướng dẫn giải:

Điều kiện xác định: $\left\{ \begin{matrix} 1 - 4x^{2} \geq 0 \\ x \neq 0 \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ x \neq 0 \\ \end{matrix} \right.\ \right.$ $\left\{ \begin{matrix} 1 - 4x^{2} \geq 0 \\ x \neq 0 \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ x \neq 0 \\ \end{matrix} \right.\ \right.$

Cách 1: Sử dụng nhân liên hợp:

Bất phương trình $\Leftrightarrow \frac{(1 - \sqrt{1 - 4x^{2}})\left( 1 + \sqrt{1 - 4x^{2}} \right)}{x\left( 1 + \sqrt{1 - 4x^{2}} \right)} < 3$ $\Leftrightarrow \frac{(1 - \sqrt{1 - 4x^{2}})\left( 1 + \sqrt{1 - 4x^{2}} \right)}{x\left( 1 + \sqrt{1 - 4x^{2}} \right)} < 3$

$\Leftrightarrow 4x < 3\left( 1 + \sqrt{1 - 4x^{2}} \right)$ $\Leftrightarrow 4x < 3\left( 1 + \sqrt{1 - 4x^{2}} \right)$

$\Leftrightarrow 3\sqrt{1 - 4x^{2}} > 4x - 3 \Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} 4x - 3 < 0 \\ 1 - 4x^{2} \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} 4x - 3 \geq 0 \\ 9(1 - 4x^{2}) > (4x - 3)^{2} \\ \end{matrix} \right.\ \\ \end{matrix} \right.$ $\Leftrightarrow 3\sqrt{1 - 4x^{2}} > 4x - 3 \Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} 4x - 3 < 0 \\ 1 - 4x^{2} \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} 4x - 3 \geq 0 \\ 9(1 - 4x^{2}) > (4x - 3)^{2} \\ \end{matrix} \right.\ \\ \end{matrix} \right.$

$\Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} x < \dfrac{3}{4} \\ x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} x \geq \dfrac{3}{4} \\ 0 < x < \dfrac{6}{13} \\ \end{matrix} \right.\ \\ \end{matrix} \right.$ $\Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} x < \dfrac{3}{4} \\ x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} x \geq \dfrac{3}{4} \\ 0 < x < \dfrac{6}{13} \\ \end{matrix} \right.\ \\ \end{matrix} \right.$kết hợp điều kiện $\Leftrightarrow \left\{ \begin{matrix} x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ x \neq 0 \\ \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} x \in \left\lbrack \dfrac{- 1}{2},\dfrac{1}{2} \right\rbrack \\ x \neq 0 \\ \end{matrix} \right.$

Cách 2: Xét các trường hợp điều kiện:

Trường hợp 1: Với $\frac{- 1}{2} \leq x < 0$ $\frac{- 1}{2} \leq x < 0$

Ta có:

Bất phương trình $\Leftrightarrow \sqrt{1 - 4x^{2}} < 1 - 3x$ $\Leftrightarrow \sqrt{1 - 4x^{2}} < 1 - 3x$

$\Leftrightarrow \left\{ \begin{matrix} 1 - 3x > 0 \\ 1 - 4x^{2} < (1 - 3x)^{2} \\ \end{matrix} \right.\ \Leftrightarrow \frac{- 1}{2} \leq x < 0$ $\Leftrightarrow \left\{ \begin{matrix} 1 - 3x > 0 \\ 1 - 4x^{2} < (1 - 3x)^{2} \\ \end{matrix} \right.\ \Leftrightarrow \frac{- 1}{2} \leq x < 0$

Trường hợp 2: Với $0 < x \leq \frac{1}{2}$ $0 < x \leq \frac{1}{2}$

Bất phương trình $\Leftrightarrow \sqrt{1 - 4x^{2}} < 1 - 3x$ $\Leftrightarrow \sqrt{1 - 4x^{2}} < 1 - 3x$

$\Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} 1 - 3x < 0 \\ 1 - 4x^{2} \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} 1 - 3x \geq 0 \\ 1 - 4x^{2} > (1 - 3x)^{2} \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Leftrightarrow 0 < x \leq \frac{1}{2}$ $\Leftrightarrow \left\lbrack \begin{matrix} \left\{ \begin{matrix} 1 - 3x < 0 \\ 1 - 4x^{2} \geq 0 \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} 1 - 3x \geq 0 \\ 1 - 4x^{2} > (1 - 3x)^{2} \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Leftrightarrow 0 < x \leq \frac{1}{2}$

Bài tập 6: Giải bất phương trình: $\sqrt{2\left( x^{2} - 1 \right)} \leq x + 1$ $\sqrt{2\left( x^{2} - 1 \right)} \leq x + 1$

Hướng dẫn giải

Điều kiện xác định: $x^{2} - 1 \geq 0 \Leftrightarrow x\mathbb{\in R}\backslash( - 1,1)$ $x^{2} - 1 \geq 0 \Leftrightarrow x\mathbb{\in R}\backslash( - 1,1)$

Bất phương trình $\Leftrightarrow \left\{ \begin{matrix} x + 1 \geq 0 \\ 2\left( x^{2} - 1 \right) < (x + 1)^{2} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \geq - 1 \\ x \in (3, - 1) \\ \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} x + 1 \geq 0 \\ 2\left( x^{2} - 1 \right) < (x + 1)^{2} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \geq - 1 \\ x \in (3, - 1) \\ \end{matrix} \right.$

Kết hợp với điều kiện đề bài $\Rightarrow x \in \lbrack 1,3)$ $\Rightarrow x \in \lbrack 1,3)$

Vậy tập nghiệm của bất phương trình là: $x \in \lbrack 1,3)$ $x \in \lbrack 1,3)$

3. Bài tập vận dụng giải bất phương trình

Bài tập 1. Giải các bất phương trình bậc hai:

a) $x^{2} - 1 \geq 0$ $x^{2} - 1 \geq 0$ b) $x^{2} - 2x - 1 < 0$ $x^{2} - 2x - 1 < 0$

c) $- 3x^{2} + 12x + 1 \leq 0$ $- 3x^{2} + 12x + 1 \leq 0$ d) $5x^{2} + x + 1 \geq 0$ $5x^{2} + x + 1 \geq 0$

Bài tập 2: Giải các bất phương trình sau:

a) $- 3x^{2} + 2x + 1 < 0$ $- 3x^{2} + 2x + 1 < 0$ b) $- 36x^{2} + 12x - 1 \geq 0$ $- 36x^{2} + 12x - 1 \geq 0$

Bài tập 3: Tìm tập xác định của hàm số: $y = \sqrt{x^{2} - 2x + 5}$ $y = \sqrt{x^{2} - 2x + 5}$

Bài tập 4. Giải bất phương trình $(x^{2} - x)^{2} + 3(x^{2} - x) + 2 \geq 0$ $(x^{2} - x)^{2} + 3(x^{2} - x) + 2 \geq 0$

Bài tập 5: Tìm tập nghiệm của các bất phương trình sau:

a) $- 3x^{2} + 2x + 1 < 0$ $- 3x^{2} + 2x + 1 < 0$

A. $S = ( - \infty; - \frac{1}{3})$ $S = ( - \infty; - \frac{1}{3})$ B. $S = (1; + \infty)$ $S = (1; + \infty)$

C. $S = \left( - \frac{1}{3};1 \right)$ $S = \left( - \frac{1}{3};1 \right)$ D. $S = ( - \infty; - \frac{1}{3}) \cup (1; + \infty)$ $S = ( - \infty; - \frac{1}{3}) \cup (1; + \infty)$

b) $x^{2} + x - 12 < 0$ $x^{2} + x - 12 < 0$

A. $S = ( - 4;3)$ B. $S = ( - \infty; - 4)$ $S = ( - \infty; - 4)$ C. $S = (3; + \infty)$ $S = (3; + \infty)$ D. $S\mathbb{= R}$ $S\mathbb{= R}$

c) $5x^{2} - 6\sqrt{5}x + 9 > 0$ $5x^{2} - 6\sqrt{5}x + 9 > 0$

A. $S\mathbb{= R}\backslash\left\{ -\frac{3\sqrt{5}}{5}\right\}$ $S\mathbb{= R}\backslash\left\{ -\frac{3\sqrt{5}}{5}\right\}$ B. $S\mathbb{= R}\backslash\left\{ \pm \frac{3\sqrt{5}}{5} \right\}$ $S\mathbb{= R}\backslash\left\{ \pm \frac{3\sqrt{5}}{5} \right\}$ C. $S\mathbb{= R}\backslash\left\{ \frac{3\sqrt{5}}{5} \right\}$ $S\mathbb{= R}\backslash\left\{ \frac{3\sqrt{5}}{5} \right\}$ D. $S=\mathbb{R}$ $S=\mathbb{R}$

d) $- 36x^{2} + 12x - 1 \geq 0$ $- 36x^{2} + 12x - 1 \geq 0$

A. $S = \left\{ \pm \frac{1}{6} \right\}$ $S = \left\{ \pm \frac{1}{6} \right\}$ B. $S = \left( -\infty;\frac{1 }{6} \right)$ $S = \left( -\infty;\frac{1 }{6} \right)$ C. $S = \left\{ \frac{1}{6} \right\}$ $S = \left\{ \frac{1}{6} \right\}$ D. $S = \left( \frac{1}{6}; + \infty \right)$ $S = \left( \frac{1}{6}; + \infty \right)$

Bài tập 6: Tìm tập nghiệm của các bất phương trình sau:

a) $- 2x^{2} + 3x - 1 \geq 0$ $- 2x^{2} + 3x - 1 \geq 0$

A. $T = \left( \frac{1}{2};1 \right)$ $T = \left( \frac{1}{2};1 \right)$ B. $T = \left( -\infty;\frac{1}{ 2} \right)$ $T = \left( -\infty;\frac{1}{ 2} \right)$ C. $T = \left\lbrack \frac{1}{2};1 \right\rbrack$ $T = \left\lbrack \frac{1}{2};1 \right\rbrack$ D. $T = (1; +\infty)$ $T = (1; +\infty)$

b) $\frac{1}{4}x^{2} - x + 1 \leq 0$ $\frac{1}{4}x^{2} - x + 1 \leq 0$

A. $T = \left\{ 3 \right\}$ $T = \left\{ 3 \right\}$ B. $T = \left\{ 4 \right\}$ $T = \left\{ 4 \right\}$ C. $T = (2;3)$ D. $T = \left\{ 2 \right\}$ $T = \left\{ 2 \right\}$

c) $- 2x^{2} + x - 1 \leq 0$ $- 2x^{2} + x - 1 \leq 0$.

A. $T\mathbb{= R}$ $T\mathbb{= R}$ B. $T\mathbb{= R}\backslash\left\{1 \right\}$ $T\mathbb{= R}\backslash\left\{1 \right\}$ C. $T = ( - 1; + \infty)$ $T = ( - 1; + \infty)$ D. $T\mathbb{= R}\backslash(3;7)$ $T\mathbb{= R}\backslash(3;7)$

d) $7x > 2x^{2} - 6$ $7x > 2x^{2} - 6$

A. $\left( \frac{3}{2};2 \right)$ $\left( \frac{3}{2};2 \right)$ B. $\left\lbrack \frac{3}{2};2 \right\rbrack$ $\left\lbrack \frac{3}{2};2 \right\rbrack$ C. $\left( -\infty;\frac{3}{2}\right)$ $\left( -\infty;\frac{3}{2}\right)$ D. $(2; + \infty)$ $(2; + \infty)$

e) $x^2 - 22x + 51 < 0$

A. $T = \varnothing$ $T = \varnothing$ B. $T\mathbb{= R}$ $T\mathbb{= R}$ C. $T = \left( 9;\frac{170}{3} \right)$ $T = \left( 9;\frac{170}{3} \right)$ D. $T = ( - \infty;2)$ $T = ( - \infty;2)$

f) $x^{2} + 5x + 6 \geq 0$ $x^{2} + 5x + 6 \geq 0$

A. $T = ( - \infty; - 3\rbrack \cup \lbrack - 2; + \infty)$ $T = ( - \infty; - 3\rbrack \cup \lbrack - 2; + \infty)$ B. $T = ( - \infty; - 3\rbrack$ $T = ( - \infty; - 3\rbrack$

C. $T = \lbrack - 3; - 2\rbrack$ $T = \lbrack - 3; - 2\rbrack$ D. $T = \lbrack - 2; + \infty)$ $T = \lbrack - 2; + \infty)$

Bài tập 7: Tìm tập xác định của hàm số $y = \sqrt{x^{2} - 3x + 2} + \frac{1}{\sqrt{x + 3}}$ $y = \sqrt{x^{2} - 3x + 2} + \frac{1}{\sqrt{x + 3}}$

Bài tập 8: Giải bất phương trình: $(x - 1)\left( x^{2} + 5x + 4 \right) \geq 0$ $(x - 1)\left( x^{2} + 5x + 4 \right) \geq 0$

Bài tập 9: Giải bất phương trình : $\frac{x^{2} + x - 1}{x - 2} > \frac{1}{x^{2} - x} + \frac{x^{3} - 2x}{x^{2} - 3x + 2}$ $\frac{x^{2} + x - 1}{x - 2} > \frac{1}{x^{2} - x} + \frac{x^{3} - 2x}{x^{2} - 3x + 2}$.

Bài tập 10: Giải bất phương trình: $(x^{2} - 4)(x^{2} + 2x) \leq 3(x^{2} + 4x + 4)$ $(x^{2} - 4)(x^{2} + 2x) \leq 3(x^{2} + 4x + 4)$.

Bài tập 11: Tìm tập nghiệm của các bất phương trình sau:

a) $(1 - 2x)\left( x^{2} - x - 1 \right) > 0$ $(1 - 2x)\left( x^{2} - x - 1 \right) > 0$

A. $S = \left( \frac{1 + \sqrt{5}}{2}; + \infty \right)$ $S = \left( \frac{1 + \sqrt{5}}{2}; + \infty \right)$ B. $S = \left(\frac{1 - \sqrt{5}}{2};\frac{1 }{2} \right)$ $S = \left(\frac{1 - \sqrt{5}}{2};\frac{1 }{2} \right)$

C. $S = \left( \frac{1 - \sqrt{5}}{2};\frac{1}{2} \right) \cup \left( \frac{1 + \sqrt{5}}{2}; + \infty \right)$ $S = \left( \frac{1 - \sqrt{5}}{2};\frac{1}{2} \right) \cup \left( \frac{1 + \sqrt{5}}{2}; + \infty \right)$ D. $S = \left( \frac{1}{2};\frac{1 + \sqrt{5}}{2} \right)$ $S = \left( \frac{1}{2};\frac{1 + \sqrt{5}}{2} \right)$

b) $x^{4} - 5x^{2} + 2x + 3 \leq 0$ $x^{4} - 5x^{2} + 2x + 3 \leq 0$

A. $S = \left\lbrack \frac{- 1 - \sqrt{13}}{2};\frac{1 - \sqrt{5}}{2} \right\rbrack$ $S = \left\lbrack \frac{- 1 - \sqrt{13}}{2};\frac{1 - \sqrt{5}}{2} \right\rbrack$ B. $S = \left\lbrack \frac{- 1 + \sqrt{13}}{2};\frac{1 + \sqrt{5}}{2} \right\rbrack$ $S = \left\lbrack \frac{- 1 + \sqrt{13}}{2};\frac{1 + \sqrt{5}}{2} \right\rbrack$

C. $S = \left\lbrack \frac{- 1 - \sqrt{13}}{2};\frac{1 - \sqrt{5}}{2} \right\rbrack \cup \left\lbrack \frac{- 1 + \sqrt{13}}{2};\frac{1 + \sqrt{5}}{2} \right\rbrack$ $S = \left\lbrack \frac{- 1 - \sqrt{13}}{2};\frac{1 - \sqrt{5}}{2} \right\rbrack \cup \left\lbrack \frac{- 1 + \sqrt{13}}{2};\frac{1 + \sqrt{5}}{2} \right\rbrack$ D. $S = \varnothing$ $S = \varnothing$

Bài tập 12: Giải các bất phương trình :

a) $\frac{x^{2} - 1}{\left( x^{2} - 3 \right)\left( - 3x^{2} + 2x + 8 \right)} > 0$ $\frac{x^{2} - 1}{\left( x^{2} - 3 \right)\left( - 3x^{2} + 2x + 8 \right)} > 0$

A. $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup ( - 1;1)$ $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup ( - 1;1)$ B. $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup \left( \sqrt{3};2 \right)$ $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup \left( \sqrt{3};2 \right)$

C. $S = ( - 1;1) \cup \left( \sqrt{3};2 \right)$ $S = ( - 1;1) \cup \left( \sqrt{3};2 \right)$ D. $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup ( - 1;1) \cup \left( \sqrt{3};2 \right)$ $S = \left( - \sqrt{3}; - \frac{4}{3} \right) \cup ( - 1;1) \cup \left( \sqrt{3};2 \right)$

b) $x^{2} + 10 \leq \frac{2x^{2} + 1}{x^{2} - 8}$ $x^{2} + 10 \leq \frac{2x^{2} + 1}{x^{2} - 8}$

A. $S = (2\sqrt{2};3\rbrack$ $S = (2\sqrt{2};3\rbrack$ B. $S = \lbrack - 3; - 2\sqrt{2})$ $S = \lbrack - 3; - 2\sqrt{2})$

C. $S = \lbrack - 3; - 2\sqrt{2}) \cup (2\sqrt{2};3\rbrack$ $S = \lbrack - 3; - 2\sqrt{2}) \cup (2\sqrt{2};3\rbrack$ D. $S\mathbb{= R}\backslash\left\{ \pm \sqrt{8} \right\}$ $S\mathbb{= R}\backslash\left\{ \pm \sqrt{8} \right\}$

Đáp án bài tập vận dụng

Bài tập 1

a) Dễ thấy $f(x) = x^{2} - 1$ $f(x) = x^{2} - 1$ có $\Delta$ $\Delta' = 1 > 0,a = 1 > 0$ và có hai nghiệm phân biệt $x_{1} = - 1;\ x_{2} = 1$ $x_{1} = - 1;\ x_{2} = 1$.

Do đó ta có bảng xét dấu $f(x)$:

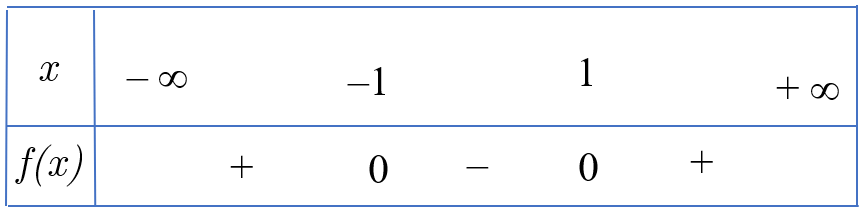
Nên bất phương trình $x^{2} - 1 \geq 0$ $x^{2} - 1 \geq 0$ có tập nghiệm là $S = ( - \infty; - 1) \cup (1; + \infty)$ $S = ( - \infty; - 1) \cup (1; + \infty)$.

b) Dễ thấy $g(x) = x^{2} - 2x - 1$ $g(x) = x^{2} - 2x - 1$ có $\Delta$ $\Delta' = 2 > 0,a = 1 > 0$ và có hai nghiệm phân biệt $x_{1} = 1 - \sqrt{2};$ $x_{1} = 1 - \sqrt{2};$ $x_{2} = 1 + \sqrt{2}$ $x_{2} = 1 + \sqrt{2}$.

Do đó ta có bảng xét dấu $g(x)$:

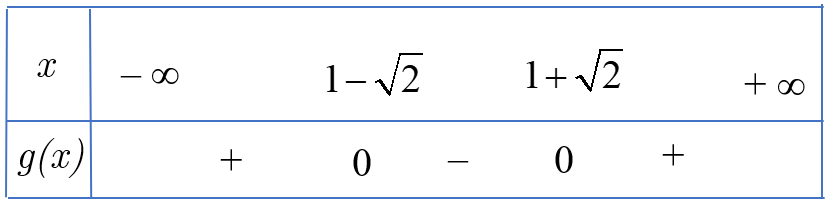
Nên bất phương trình $x^{2} - 2x - 1 < 0$ $x^{2} - 2x - 1 < 0$ có tập nghiệm là $S = \left( 1 - \sqrt{2};1 + \sqrt{2} \right)$ $S = \left( 1 - \sqrt{2};1 + \sqrt{2} \right)$.

c) Dễ thấy $h(x) = - 3x^{2} + 12x + 1$ $h(x) = - 3x^{2} + 12x + 1$ có $\Delta$ $\Delta' = 39 > 0,a = - 3 < 0$ và có hai nghiệm phân biệt $x_{1} = \frac{6 + \sqrt{39}}{3};$ $x_{1} = \frac{6 + \sqrt{39}}{3};$ $x_{2} = \frac{6 - \sqrt{39}}{3}$ $x_{2} = \frac{6 - \sqrt{39}}{3}$.

Do đó ta có bảng xét dấu $h(x)$:

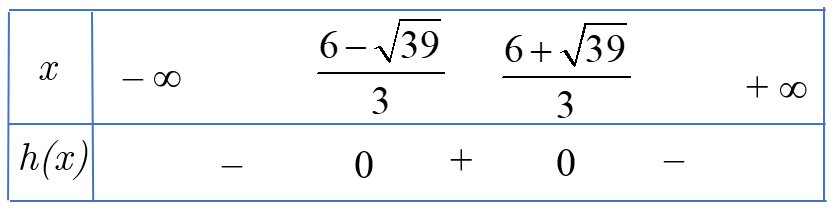
Nên bất phương trình $- 3x^{2} + 12x + 1 \leq 0$ $- 3x^{2} + 12x + 1 \leq 0$ có tập nghiệm là $S = \left( - \infty;\frac{6 - \sqrt{39}}{3} \right) \cup \left( \frac{6 + \sqrt{39}}{3}; + \infty \right)$ $S = \left( - \infty;\frac{6 - \sqrt{39}}{3} \right) \cup \left( \frac{6 + \sqrt{39}}{3}; + \infty \right)$.

d) $k(x) = 5x^{2} + x + 1$ $k(x) = 5x^{2} + x + 1$ có $\Delta = - 19 < 0$ $\Delta = - 19 < 0$ và $a = 5 > 0$ nên $k(x) > 0$ với mọi $x\mathbb{\in R}.$ $x\mathbb{\in R}.$

Từ đó suy ra bất phương trình $5x^{2} + x+ 1 \geq 0$ $5x^{2} + x+ 1 \geq 0$ có tập nghiệm là $\mathbb{R}$ $\mathbb{R}$.

Bài tập 2

a) Tam thức $f(x) = - 3x^{2} + 2x + 1$ $f(x) = - 3x^{2} + 2x + 1$ có $a = - 3 < 0$ và có hai nghiệm $x_{1} = - \frac{1}{3};$ $x_{1} = - \frac{1}{3};$ $x_{2} = 1$ $x_{2} = 1$ ($f(x)$ cùng dấu với hệ số $a$).

Suy ra $- 3x^{2} + 2x + 1 < 0 \Leftrightarrow x < - \frac{1}{3}$ $- 3x^{2} + 2x + 1 < 0 \Leftrightarrow x < - \frac{1}{3}$ hoặc $x > 1$

Vậy tập nghiệm của bất phương trình: $S = ( - \infty; - \frac{1}{3}) \cup (1; + \infty)$ $S = ( - \infty; - \frac{1}{3}) \cup (1; + \infty)$.

b) Tam thức $f(x) = - 36x^{2} + 12x - 1$ $f(x) = - 36x^{2} + 12x - 1$ có $a = - 36 < 0$ và $\Delta = 0$ $\Delta = 0$

$f(x)$ trái dấu với hệ số $a$ nên $f(x)$ âm với $\forall x \neq \frac{1}{6}$ $\forall x \neq \frac{1}{6}$ và $f\left( \frac{1}{6} \right) = 0$ $f\left( \frac{1}{6} \right) = 0$

Suy ra $- 36x^{2} + 12x - 1 \geq 0 \Leftrightarrow x = \frac{1}{6}$ $- 36x^{2} + 12x - 1 \geq 0 \Leftrightarrow x = \frac{1}{6}$

Vậy tập nghiệm của bất phương trình là $S = \left\{ \frac{1}{6} \right\}$ $S = \left\{ \frac{1}{6} \right\}$.

Bài tập 3

Điều kiện: $x^{2} - 2x + 5 \geq 0$ $x^{2} - 2x + 5 \geq 0$

Xét tam thức vế trái có $\Delta$ $\Delta' = - 4 < 0$ và $a = 1 > 0$ nên $x^{2} - 2x + 5 > 0,\ \ \forall x\mathbb{\in R}$ $x^{2} - 2x + 5 > 0,\ \ \forall x\mathbb{\in R}$.

Vậy tập xác định của hàm số $D\mathbb{= R}$ $D\mathbb{= R}$.

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

--------------------------------------------------------

Dạng toán tìm tập nghiệm của bất phương trình là bước đệm quan trọng để học tốt các phần tiếp theo của chương trình Toán lớp 10. Khi đã nắm chắc các quy tắc biến đổi, so sánh và biểu diễn nghiệm, bạn sẽ dễ dàng xử lý nhanh những bài toán khó hơn và đạt điểm tối đa trong các bài kiểm tra.

Hy vọng bài viết đã giúp bạn hình dung rõ ràng phương pháp giải, cách trình bày và các lỗi thường gặp cần tránh. Đừng quên luyện tập thường xuyên với các bài tập có đáp án để củng cố kỹ năng và tăng tốc độ giải.

Chúc bạn học tốt, đạt kết quả cao và luôn tự tin khi đối diện các dạng bất phương trình trong Toán lớp 10 và những lớp học tiếp theo!

Tải về

Chọn file muốn tải về: