Giải bài tập trang 87, 88 SGK Đại số 10: Bất phương trình và hệ bất phương trình một ẩn

Giải bài tập Toán 10

Giải bài tập trang 87, 88 SGK Đại số 10: Bất phương trình và hệ bất phương trình một ẩn

Bài 1 trang 87 SGK Đại số lớp 10
Bài 2 trang 88 SGK Đại số lớp 10
Bài 3 trang 88 SGK Đại số lớp 10
Bài 4 trang 88 SGK Đại số lớp 10
Bài 5 trang 88 SGK Đại số lớp 10

Giải bài tập trang 87, 88 SGK Đại số 10: Bất phương trình và hệ bất phương trình một ẩn là tài liệu tham khảo giúp các em ôn luyện, củng cố các kiến thức giải Toán. Sau đây mời các em cùng tham khảo chi tiết và tải về lời giải chi tiết dưới đây nhé.

Trắc nghiệm trực tuyến: Đề kiểm tra 15 phút môn Đại số lớp 10 - Đại cương về bất phương trình

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 10, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 10 sau: Nhóm Tài liệu học tập lớp 10. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Giải bài 1, 2, 3, 4, 5 trang 87, 88 SGK Đại số 10: Bất phương trình và hệ bất phương trình một ẩn

Bài 1 trang 87 SGK Đại số lớp 10

Tìm các giá trị x thỏa mãn điều kiện của mỗi bất phương trình sau:

Giải bài tập trang 87, 88 SGK Đại số 10: Bất phương trình và hệ bất phương trình một ẩn

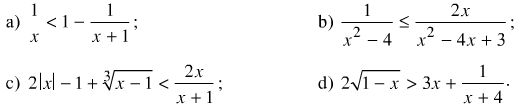
Hướng dẫn giải

Điều kiện xác định của phân thức _{$\frac{A}{B}$} là _{$B\ne 0$}

Điều kiện xác định của căn thức là _$\sqrt{C}$ là _{$C\ge 0$}

Đáp án và hướng dẫn giải bài 1:

a) Điều kiện xác định: D = {x ∈ R/x ≠ 0 và x + 1 ≠ 0} = R\{0;-1}.

b) Điều kiện xác định: D = {x ∈ R/x² – 4 ≠ 0 và x² – 4x + 3 ≠ 0} = R\{±2; 1; 3}.

c) Điều kiện xác định: D = R\{-1}.

d) Điều kiện xác định: D = {x ∈ R/x + 4 ≠ 0 và 1 – x ≥ 0} = (-∞; – 4) ∪ (- 4; 1].

Bài 2 trang 88 SGK Đại số lớp 10

Chứng minh các bất phương trình sau vô nghiệm.

$a){{x}^{2}}+\sqrt{x+8}\le -3$ $a){{x}^{2}}+\sqrt{x+8}\le -3$

$b)\sqrt{1+2{{\left( x-3 \right)}^{2}}}+\sqrt{5-4x+{{x}^{2}}}<\frac{3}{2};$ $b)\sqrt{1+2{{\left( x-3 \right)}^{2}}}+\sqrt{5-4x+{{x}^{2}}}<\frac{3}{2};$

$c)\sqrt{1+{{x}^{2}}}-\sqrt{7+{{x}^{2}}}>1;$ $c)\sqrt{1+{{x}^{2}}}-\sqrt{7+{{x}^{2}}}>1;$

Hướng dẫn giải

Sử dụng phương pháp đánh giá đa thức.

$\sqrt{a}\ge 0,\forall a\ge 0$ $\sqrt{a}\ge 0,\forall a\ge 0$
${{a}^{2}}\ge 0,\forall a$ ${{a}^{2}}\ge 0,\forall a$

Đáp án và hướng dẫn giải bài 2:

a) Gọi D là điều kiện xác định của biểu thức vế trái D = [- 8; +∞]. Vế trái dương với mọi x ∈ D trong khi vế phải là số âm. Mệnh đề sai với mọi x ∈ D. Vậy bất phương trình vô nghiệm.

b) Vế trái có

$\begin{align} & \sqrt{1+2{{\left( x-3 \right)}^{2}}}\ge 1,\forall x\in \mathbb{R} \\ & \sqrt{5-4x+{{x}^{2}}}=\sqrt{1+{{\left( x-2 \right)}^{2}}}\ge 1,\forall x\in \mathbb{R} \\ & \Rightarrow \sqrt{1+2{{\left( x-3 \right)}^{2}}}+\sqrt{5-4x+{{x}^{2}}}\ge 2,\forall x\in \mathbb{R} \\ \end{align}$ $\begin{align} & \sqrt{1+2{{\left( x-3 \right)}^{2}}}\ge 1,\forall x\in \mathbb{R} \\ & \sqrt{5-4x+{{x}^{2}}}=\sqrt{1+{{\left( x-2 \right)}^{2}}}\ge 1,\forall x\in \mathbb{R} \\ & \Rightarrow \sqrt{1+2{{\left( x-3 \right)}^{2}}}+\sqrt{5-4x+{{x}^{2}}}\ge 2,\forall x\in \mathbb{R} \\ \end{align}$

Mệnh đề sai ∀x ∈ R. Bất phương trình vô nghiệm.

c) ĐKXĐ: D = [-1; 1]. Vế trái âm với mọi x ∈ D trong khi vế phải dương.

Bài 3 trang 88 SGK Đại số lớp 10

Giải thích vì sao các cặp bất phương trình sau tương đương?

a) -4x + 1 > 0và 4x - 1 < 0;

b) $2{{x}^{2}}+5\le 2x-1$ $2{{x}^{2}}+5\le 2x-1$ và $2{{x}^{2}}-2x+6\le 0$ $2{{x}^{2}}-2x+6\le 0$;

c) x + 1 > 0 và _{$x + 1 + \frac{1}{{{x}^{2}}+1}>\frac{1}{{{x}^{2}}+1}$};

d) $\sqrt{x-1}\ge x$ $\sqrt{x-1}\ge x$ và _{$\left( 2x+1 \right)\sqrt{x-1}\ge x\left( 2x+1 \right)$;}

Hướng dẫn giải

Khi sử dụng các phép biến đổi tương đương ta nhận được các bpt tương đương.

Các phép biến đổi tương đương gồm:

+ Cộng hoặc trừ hai vế của BPT với cùng một biểu thức:

$\mathrm{P}(\mathrm{x})<\mathrm{Q}(\mathrm{x}) \Leftrightarrow \mathrm{P}(\mathrm{x})+\mathrm{f}(\mathrm{x})<\mathrm{Q}(\mathrm{x})+\mathrm{f}(\mathrm{x})$ $\mathrm{P}(\mathrm{x})<\mathrm{Q}(\mathrm{x}) \Leftrightarrow \mathrm{P}(\mathrm{x})+\mathrm{f}(\mathrm{x})<\mathrm{Q}(\mathrm{x})+\mathrm{f}(\mathrm{x})$

+ Nhân hoặc chia hai vế của BPT với cùng một biểu thức khác

_{$P(x)< Q(x) \Leftrightarrow P(x) \cdot f(x)< Q(x) \cdot f(x)$} nếu f(x)>0

$\mathrm{P}(\mathrm{x})<\mathrm{Q}(\mathrm{x}) \Leftrightarrow \mathrm{P}(\mathrm{x}) . \mathrm{f}(\mathrm{x})>\mathrm{Q}(\mathrm{x}) . \mathrm{f}(\mathrm{x})$ $\mathrm{P}(\mathrm{x})<\mathrm{Q}(\mathrm{x}) \Leftrightarrow \mathrm{P}(\mathrm{x}) . \mathrm{f}(\mathrm{x})>\mathrm{Q}(\mathrm{x}) . \mathrm{f}(\mathrm{x})$ nếu $\mathrm{f}(\mathrm{x})<0$ $\mathrm{f}(\mathrm{x})<0$

+ Nâng lên lũy thừa bậc chẵn của BPT có cả hai vế đều dương

$0<\mathrm{P}(\mathrm{x})<\mathrm{Q}(\mathrm{x}) \Leftrightarrow \mathrm{P}^{2 \mathrm{n}}(\mathrm{x})<\mathrm{Q}^{2 \mathrm{n}}(\mathrm{x})$ $0<\mathrm{P}(\mathrm{x})<\mathrm{Q}(\mathrm{x}) \Leftrightarrow \mathrm{P}^{2 \mathrm{n}}(\mathrm{x})<\mathrm{Q}^{2 \mathrm{n}}(\mathrm{x})$

+ Nâng lên lũy thừa bậc lẻ cả hai vế của BPT

$\mathrm{P}(\mathrm{x})<\mathrm{Q}(\mathrm{x}) \Leftrightarrow \mathrm{P}^{2 \mathrm{n}+1}(\mathrm{x})<\mathrm{Q}^{2 \mathrm{n}+1}(\mathrm{x})$ $\mathrm{P}(\mathrm{x})<\mathrm{Q}(\mathrm{x}) \Leftrightarrow \mathrm{P}^{2 \mathrm{n}+1}(\mathrm{x})<\mathrm{Q}^{2 \mathrm{n}+1}(\mathrm{x})$

+ Khai căn bậc hai của BPT có cả hai vế đều dương:

$0<\mathrm{P}(\mathrm{x})<\mathrm{Q}(\mathrm{x}) \Leftrightarrow \sqrt{\mathrm{P}}(\mathrm{x})<\sqrt{\mathrm{Q}}(\mathrm{x})$ $0<\mathrm{P}(\mathrm{x})<\mathrm{Q}(\mathrm{x}) \Leftrightarrow \sqrt{\mathrm{P}}(\mathrm{x})<\sqrt{\mathrm{Q}}(\mathrm{x})$

Đáp án và hướng dẫn giải bài 3:

a) Tương đương, vì nhân hai vế bất phương trình thứ nhất với -1 và đổi chiều bất phương trình thì được bất phương trình thứ 2.

b) Chuyển vế các hạng tử vế phải và đổi dấu ở bất phương trình thứ nhất thì được bất phương trình thứ hai tương đương.

c) Tương đương. Vì cộng hai vế bất phương trình thứ nhất với với mọi x ta được bất phương trình thứ 3.

d) Điều kiện xác định bất phương trình thứ nhất: D = {x ≥ 1}.

2x + 1 > 0 ∀x ∈ D. Nhân hai vế bất phương trình thứ hai. Vậy bất phương trình tương đương.

Bài 4 trang 88 SGK Đại số lớp 10

Giải các phương trình sau

a)

b) (2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x² – 5.

Hướng dẫn giải

Biến đổi biểu thức bằng các phép cộng trừ nhân chia đa thức thông thường.

Đáp án và hướng dẫn giải bài 4:

a)

$\begin{align} & \frac{3x+1}{2}-\frac{x-2}{3}-\frac{1-2x}{4}<0 \\ & \Leftrightarrow 12\left[ \frac{3x+1}{2}-\frac{x-2}{3}-\frac{1-2x}{4} \right]<0 \\ \end{align}$ $\begin{align} & \frac{3x+1}{2}-\frac{x-2}{3}-\frac{1-2x}{4}<0 \\ & \Leftrightarrow 12\left[ \frac{3x+1}{2}-\frac{x-2}{3}-\frac{1-2x}{4} \right]<0 \\ \end{align}$

<=> 6(3x + 1) – 4(x – 2) – 3(1 – 2x) < 0

<=> 20x + 11 < 0

<=> 20x < – 11

<=> x < -11/20

b) (2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x² – 5.

<=> 2x² + 5x – 3 – 3x + 1 ≤ x² + 2x – 3 + x² – 5

<=> 0x ≤ -6.

Vậy bất phương trình vô nghiệm.

Bài 5 trang 88 SGK Đại số lớp 10

Giải các hệ bất phương trình

$a. \left\{ \begin{matrix} 6x+\dfrac{5}{7}<4x+7 \\ \dfrac{8x+3}{2}<2x+5 \\ \end{matrix} \right.$ $a. \left\{ \begin{matrix} 6x+\dfrac{5}{7}<4x+7 \\ \dfrac{8x+3}{2}<2x+5 \\ \end{matrix} \right.$

$b. \left\{ \begin{matrix} 15x-2>2x+1 \\ x\left( x-4 \right)<\dfrac{3x-14}{2} \\ \end{matrix} \right.$ $b. \left\{ \begin{matrix} 15x-2>2x+1 \\ x\left( x-4 \right)<\dfrac{3x-14}{2} \\ \end{matrix} \right.$

Hướng dẫn giải

Thực hiện giải từng bất phương trình sau đó kết hợp nghiệm của các bất phương trình đã giải.

Đáp án và hướng dẫn giải bài 5:

a) 6x + 5/7 < 4x + 7 <=> 6x – 4x < 7 – 5/7

<=> x < 22/7

(8x + 3)/2 < 2x + 5 <=> 4x – 2x < 5 – 3/2

<=> x < 7/4

Tập nghiệm của hệ bất phương trình:

$S=\left( -\infty ;\frac{22}{7} \right)\cap \left( -\infty ;\frac{7}{4} \right)=\left( -\infty ;\frac{7}{4} \right)$ $S=\left( -\infty ;\frac{22}{7} \right)\cap \left( -\infty ;\frac{7}{4} \right)=\left( -\infty ;\frac{7}{4} \right)$

b) 5x – 2 > 2x + 1/3

<=> x > 7/39

$2\left( x-4 \right)<\frac{3x-14}{2}\Leftrightarrow x< 2$ $2\left( x-4 \right)<\frac{3x-14}{2}\Leftrightarrow x< 2$

Vậy tập nghiệm của bất phương trình là: $S=\left( \frac{7}{39};+\infty \right)\cap \left( -\infty ;2 \right)=\left( \frac{7}{39};2 \right)$ $S=\left( \frac{7}{39};+\infty \right)\cap \left( -\infty ;2 \right)=\left( \frac{7}{39};2 \right)$

------------------------------------------

Trên đây VnDoc đã giới thiệu tới bạn đọc tài liệu Giải bài tập trang 87, 88 SGK Đại số 10: Bất phương trình và hệ bất phương trình một ẩn. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài học rồi đúng không ạ? Hi vọng qua bài viết bạn đọc có thể học tập tốt hơn môn Toán lớp 10 nhé. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu thêm tới các bạn học sinh tài liệu Toán lớp 10, Ngữ Văn 10, Tiếng Anh lớp 10,... mà VnDoc tổng hợp và đăng tải. Chúc các bạn ôn tập thật tốt!

Chia sẻ, đánh giá bài viết

1

6.024

Bài trước

Bài sau