Giải Toán 10: Ôn tập chương 1

Giải bài tập trang 24, 25 SGK Đại số 10: Ôn tập chương 1 được VnDoc đăng tải nhằm hướng dẫn các bạn học sinh giải bài tập ôn tập chương 1 đại số 10. Qua lời giải bài tập Toán lớp 10 phần Đại Số này, các bạn có thể ôn tập các kiến thức về mệnh đề, tập hợp, các phép toán tập hợp, số gần đúng, sai số. Hi vong lời giải bài tập Toán 10 này sẽ giúp các bạn học tốt môn Toán lớp 10. Mời các bạn cùng tham khảo chi tiết và tải về tại đây nhé.

Giải bài ôn tập chương 1 Đại số lớp 10: Bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 SGK trang 24, 25

Giải bài tập Toán 10 Bài 1

Bài 1: Xác định tính đúng sai của mệnh đề phủ định ^-A theo tính đúng sai của mệnh đề A.

Hướng dẫn giải bài 1:

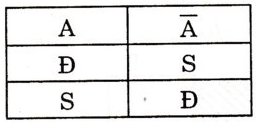
• ^-A sai nếu A đúng
• ^-A đúng nếu A sai

Giải bài tập Toán 10 Bài 2

Bài 2: Thế nào là mệnh đề đảo của mệnh A ⇒ B? Nếu A ⇒ B là mệnh đề đúng, thì mệnh đề đảo của nó có đúng không? Cho ví dụ minh họa.

Hướng dẫn giải bài 2:

Mệnh đề đảo của A ⇒ B là B ⇒ A

A ⇒ B đúng chưa chắc B ⇒ A đúng.

Ví dụ: A: hai góc đối đỉnh; B: hai góc ấy bằng nhau Ta có: A ⇒ B đúng. Xét B ⇒ A: nếu hai góc băng nhau thì hai góc ấy đối đỉnh. Mệnh đề này sai.

Giải bài tập Toán 10 Bài 3

Bài 3: Thế nào là hai mệnh đề tương đương?

Hướng dẫn giải bài 3:

Giải bài tập Toán 10 Bài 4

Bài 4: Nêu định nghĩa tập hợp con và định nghĩa hai hợp bằng nhau.

Hướng dẫn giải bài 4:

A⊂B ⇔ ∀x (x ∈ A ⇒ x ∈ B)

Giải bài tập Toán 10 Bài 5

Bài 5: Nêu các định nghĩa hợp, giao, Hiệu và phần bù của hai tập hợp. Minh họa các khái niệm đó bằng hình vẽ.

Hướng dẫn giải bài 5:

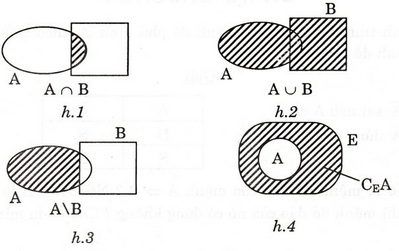
A ∩ B ⇔ ∀x (x ∈ A và x ∈ B) (h.1)

A ∪ B ⇔ ∀x (x ∈ A hoặc x ∈ B) (h.2)

A \ B ⇔ ∀x (x ∈ A hoặc x ∉ B) (h.3)

Cho A ⊂ E.C_EA = {x/x ∈ E và x ∉ A} (h.4)

Giải bài tập Toán 10 Bài 6

Bài 6: Nêu định nghĩa đoạn [a; b], khoảng (a; b), nửa khoảng [a; b), (a; b], (-∞; b], [a; +∞). Viết tập hợp R các số thực dưới dạng một khoảng.

Hướng dẫn giải bài 6:

x ∈ [a; b] ↔ a ≦ x ≦ b.

x ∈ (a; b) ↔ a < x < b.

x ∈ [a; b) ↔ a ≦ x < b.

x ∈ (a; b] ↔ a < x ≦ b.

x ∈ [a; b] ↔ a ≦ x ≦ b.

x ∈ (-∞; b] ↔ x ≦ b.

x ∈ [a; +∞] ↔ a ≦ x.

x ∈ R ↔ x ∈ (-∞; +∞).

Giải bài tập Toán 10 Bài 7

Bài 7: Thế nào là sai số tuyệt đối của một số gần đúng? Thế nào là độ chính xác của một số gần đúng?

Hướng dẫn giải bài 7:

Giải bài tập Toán 10 Bài 8

Bài 8: Cho tứ giác ABCD. Xét tính đúng sai của mệnh đề P ⇒ Q với

a) P: "ABCD là một hình vuông"

Q: "ABCD là một hình bình hành"

b) P: "ABCD là một hình thoi"

Q: "ABCD là một hình chữ nhật"

Đáp án bài 8: a) Đúng; b) Sai

Giải bài tập Toán 10 Bài 9

Bài 9: Xét mối quan hệ bao hàm giữa các tập hợp sau

A là tập hợp các hình tứ giác;

B là tập hợp các hình bình hành;

C là tập hợp các hình thang;

D là tập hợp các hình chữ nhật;

E là tập hợp các hình vuông;

G là tập hợp các hình thoi.

Hướng dẫn giải bài 9:

Hình vuông là hình chữ nhật ................. nên E ⊂ D

Hình chữ nhật là hình bình hành................. nên D ⊂ B

Hình bình hành là hình thang................. nên B ⊂ C

Hình thang là hình tứ giác ................. nên C ⊂ A

Vậy, A ⊃ C ⊃ B ⊃ D ⊃ E

Mặt khác:

– Hình vuông là hình thoi ................. nên E ⊂ G

Hình thoi là hình bình hành................... nên G ⊂ B

Vậy, A ⊃ C ⊃ B ⊃ G ⊃ E.

Giải bài tập Toán 10 Bài 10

Bài 10: Liệt kê các phần tử của mỗi tập hợp sau

a) A = {3k – 2 | k = 0, 1, 2, 3, 4, 5};

b) B = {x ∈ N |x ≤ 12}

c) C = {(1 - n)ⁿ | n ∈ N}

Hướng dẫn giải bài 10:

a) Khi:

k = 0 thì 3k - 2 = -2

k = 1 thì 3k - 2 = 1

k = 2 thì 3k - 2 = 4

k = 3 thì 3k - 2 = 7

k = 4 thì 3k - 2 = 10

k = 5 thì 3k - 2 = 13

Nên A = {-2; 1; 4; 7; 10; 13}

b) Vì x ∈ N và x ≦ 12 nên x = 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12

Vậy B = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}

c) Vì n ∈ N nên n = 0; 1; 2;...

Do đó, (-1)ⁿ = 1 khi n = 0 hay n chẵn

(-1)ⁿ = -1 khi n lẻ

Vậy, C = {-1; 1}

Giải bài tập Toán 10 Bài 11

Bài 11: Giả sử A, B là hai tập hợp số và X là một số đã cho. Tìm các cặp mệnh đề tương đương trong các mệnh đề sau

P: "x ∈ A ∪ B"; S: "x ∈ A và x ∈ B";

Q: "x ∈ A \ B"; T: "x ∈ A hoặc x ∈ B";

R: "x ∈ A ∩ B"; X:"x ∈ A hoặc x ∉ B"

Hướng dẫn giải bài 11:

P ⇔ T; R ⇔ S; Q ⇔ X

Giải bài tập Toán 10 Bài 12

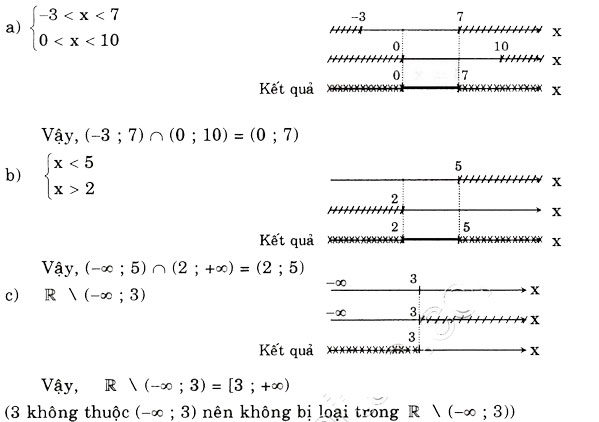
Bài 12: Xác định các tập hợp sau

a) (-3; 7) ∩ (0; 10);

b) (—∞; 5) ∩ (2; +∞);

c) R \(—∞; 3)

Hướng dẫn giải bài 12:

Giải bài tập Toán 10 Bài 13

Bài 13: Dùng máy tính bỏ túi hoặc bảng kẻ số để tìm giá trị của ³√12 Làm tròn kết quả nhận được đến chữ số thập phân thứ ba và ước lượng sai số tuyệt đối.

Hướng dẫn giải bài 13:

• Kết quả đã làm tròn: \(\sqrt[3]{12}\approx2,289\)
• Ước lượng sai số tuyệt đối: \(|2,289-2,289|<0,001\)

Giải bài tập Toán 10 Bài 14

Bài 14: Chiều cao của một ngọn đồi đo được là h = 347,13 ± 0,2m. Hãy viết số quy tròn của số gần đúng 347,13

Hướng dẫn giải bài 14:

Số quy tròn của h = 347,13 ± 0,02 (m) là h = 347.

Giải bài tập Toán 10 Bài 15

Bài 15: Những quan hệ nào trong các quan hệ sau là đúng?

a) A ⊂ A ∪ B;                  b) A ⊂ A ∩ B;

c) A ∩ B ⊂ A ∪ B;           d) A ∪ B ⊂ B;

e) A ∩ B ⊂ A.

Hướng dẫn giải bài 15:

a. Đúng

b. Sai (vì X ∈ A không thể suy ra X ∈ A ∩ B)

Trên đây VnDoc đã chia sẻ Giải Toán 10: Ôn tập chương 1. Chắc hẳn qua bài viết bạn đọc có thể nắm bắt được những hướng dẫn giải bài tập trong ôn tập chương 1. Bài viết tổng hợp hướng dẫn giải chi tiết từ bài 1 đến bài 15 ôn tập chương 1 qua đây rèn luyện cho chúng ta cách xác định tính đúng sai của mệnh đề, cách xác định các tập hợp... Hy vọng với tài liệu này sẽ giúp ích cho các bạn học sinh tham khảo, chuẩn bị cho bài giảng sắp tới tốt hơn nhé.

• Giải Toán 10 bài 1: Mệnh đề
• Giải bài tập SGK Toán lớp 10 (Đại số) chương 1: Các phép toán tập hợp
• Giải bài tập SGK Toán lớp 10 (Đại số) chương 1: Các tập hợp số
• Giải bài tập trang 23 SGK Đại số 10: Số gần đúng - Sai số
• Giải bài tập trang 38, 39 SGK Đại số 10 chương 2: Hàm số

.........................................

Ngoài Giải Toán 10: Ôn tập chương 1. Để giúp bạn đọc học tập tốt hơn, VnDoc.com mời bạn đọc cùng tham khảo một số tài liệu được chúng tôi biên soạn và tổng hợp, mời các bạn tham khảo đề thi học kì 1 lớp 10, đề thi học kì 2 lớp 10 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 10 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt