Giải bài tập Hình học 10 bài 2: Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ

VnDoc.com xin giới thiệu tới bạn đọc tài liệu: Giải bài tập Hình học 10 bài 2: Tích vô hướng của hai vectơ, với bộ câu hỏi bài tập trong SKG trang 45 Toán 10 có lời giải. Lời giải bài tập Toán 10 Hình học này sẽ giúp các bạn học sinh rèn luyện cách giải bài tập Toán 10 một cách hiệu quả. VnDoc.com mời các bạn học sinh và thầy cô tham khảo.

Giải bài tập Hình học 10 bài 2: Tích vô hướng của hai vectơ

Bài 1 (trang 45 SGK Hình học 10): Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng

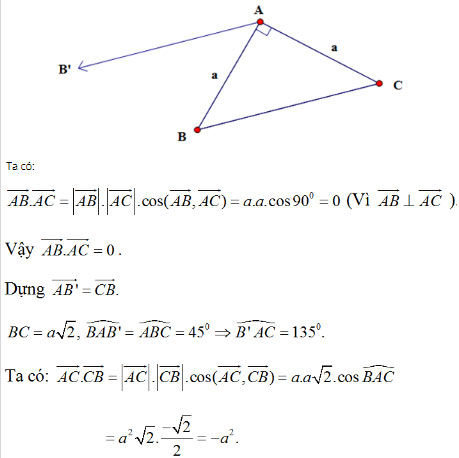
Bài 2 (trang 45 SGK Hình học 10): Cho ba điểm O, A, B thẳng hàng và biết OA = a, OB = b. Tính tích vô hướng

OA^→, OB^→

trong hai trường hợp:

a) Điểm O nằm ngoài đoạn AB;

b) Điểm O nằm trong đoạn AB.

Bài 3 (trang 45 SGK Hình học 10): Cho nửa hình tròn tâm O có đường kính AB=2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho hai dây cung AM và BN cắt nhau tại I.

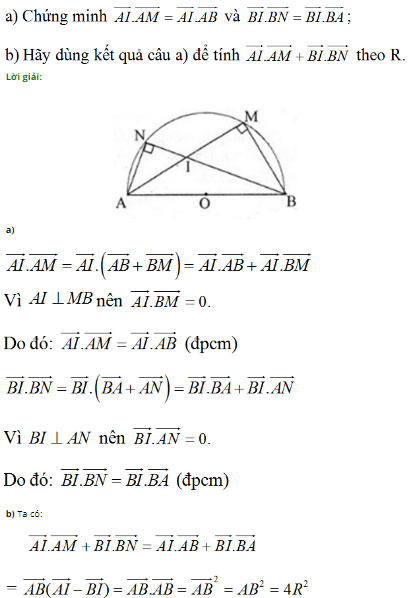
Bài 4 (trang 45 SGK Hình học 10): Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(1; 2).

a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;

b) Tính chu vi tam giác OAB.

c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.

Lời giải:

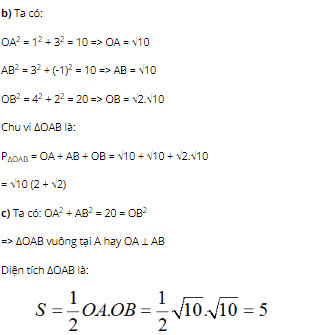
Bài 5 (trang 46 SGK Hình học 10): Trên mặt phẳng Oxy hãy tính góc giữa hai vectơ a^→ và b^→ trong các trường hợp sau:

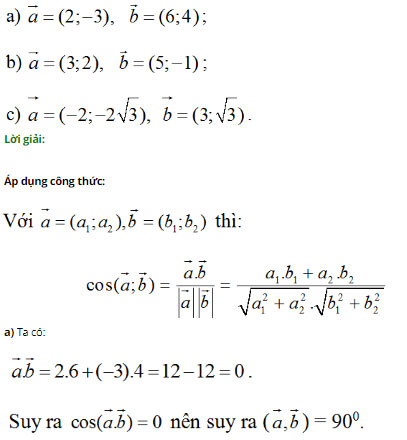
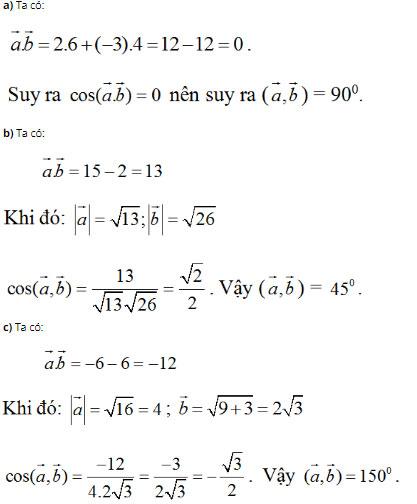
Bài 6 (trang 46 SGK Hình học 10): Trên mặt phẳng tọa độ Oxy cho bốn điểm: A(7; -3), B(8; 4), C(1; 5), D(0; –2). Chứng minh rằng tứ giác ABCD là hình vuông.

Lời giải:

Ta có:

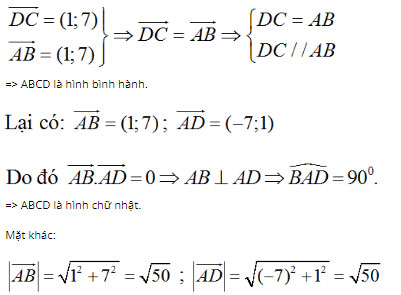
Bài 7 (trang 46 SGK Hình học 10): Trên mặt phẳng Oxy cho điểm A(-2; 1). Gọi B là điểm đối xứng với điểm A qua gốc tọa độ O. Tìm tọa độ của điểm C có tung độ bằng 2 sao cho tam giác vuông ở C.

Lời giải:

Vì B đối xứng với A(-2; 1) qua O nên ta có: B(2; -1)

Gọi tọa độ C(x; 2).

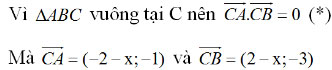
Nên (*) ⇔ -(2 + x)(2 - x) + 3 = 0

⇔ -4 + x² + 3 = 0

⇔ x² = 1 ⇔ x = ±1

Vậy C(1; 2) hay C(-1; 2).