VnDoc.com

Giải bài tập Hình học 10 bài 3: Các hệ thức lượng trong tam giác và giải tam giác

Để học tốt Toán lớp 10

Bài trước

Bài sau

Các hệ thức lượng trong tam giác và giải tam giác

Bài 1 trang 59 SGK Hình học 10
Bài 2 trang 59 SGK Hình học 10
Bài 3 trang 59 SGK Hình học 10
Bài 4 trang 59 SGK Hình học 10
Bài 5 trang 59 SGK Hình học 10
Bài 6 trang 59 SGK Hình học 10
Bài 7 trang 59 SGK Hình học 10
Bài 8 trang 59 SGK Hình học 10
Bài 9 trang 59 SGK Hình học 10
Bài 10 trang 60 SGK Hình học 10
Bài 11 trang 60 SGK Hình học 10

VnDoc.com xin giới thiệu tới bạn đọc tài liệu Giải bài tập Hình học 10 bài 3: Các hệ thức lượng trong tam giác và giải tam giác để bạn đọc cùng tham khảo. Bài viết giải bài tập Toán 10 Hình học này chắc chắn sẽ giúp các bạn học sinh giải bài tập Toán 10 một cách hiệu quả hơn. VnDoc.com mời các bạn học sinh và thầy cô tham khảo chi tiết bài viết dưới đây nhé.

Giải bài tập Hình học 10 bài 3: Các hệ thức lượng trong tam giác và giải tam giác

Bài 1 trang 59 SGK Hình học 10

Cho tam giác ABC vuông tại A, ∠B = 58^o và cạnh a = 72cm. Tính ∠C, cạnh b và đường cao h.

Lời giải:

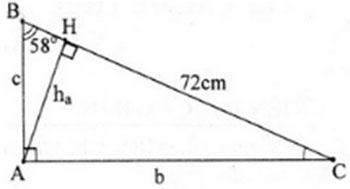
Các hệ thức lượng trong tam giác và giải tam giác

- Ta có: ∠C = 90^o - ∠B = 90^o - 58^o = 32^o

- Ta có: b = BC.sin58^o = a.sin58^o = 61,06 (cm)

- Ta có: c = BC.cos58^o = a.cos58^o = 38,15 (cm)

Do đó:

$h_a=\frac{AB.AC}{BC}=\frac{c.b}{a}=\frac{38,15.61,06}{72}=\ 32,35\ \left(cm\right)$ $h_a=\frac{AB.AC}{BC}=\frac{c.b}{a}=\frac{38,15.61,06}{72}=\ 32,35\ \left(cm\right)$

Bài 2 trang 59 SGK Hình học 10

Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc ∠A, ∠B, ∠C.

Lời giải:

$cos\hat{A} = \frac{b^2 + c^2 - a^2}{2bc} = \frac{85^2+54^2-52,1^2}{2.85.54} =0.81\Rightarrow \hat{A}=36^o$ $cos\hat{A} = \frac{b^2 + c^2 - a^2}{2bc} = \frac{85^2+54^2-52,1^2}{2.85.54} =0.81\Rightarrow \hat{A}=36^o$

$cos\hat{B} = \frac{c^2 + a^2 - b^2}{2ac} = \frac{54^2+52,1^2-85,1^2}{2.54.52,1} =-0.28\Rightarrow \hat{B}=106^o28$ $cos\hat{B} = \frac{c^2 + a^2 - b^2}{2ac} = \frac{54^2+52,1^2-85,1^2}{2.54.52,1} =-0.28\Rightarrow \hat{B}=106^o28'$

$=>\ \angle C\ =\ 180^o-\angle A\ -\angle B=37^o32$ $=>\ \angle C\ =\ 180^o-\angle A\ -\angle B=37^o32'$

Bài 3 trang 59 SGK Hình học 10

Cho tam giác ABC có ∠A = 120^o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc ∠B, ∠C của tam giác đó.

Lời giải:

- Ta có: a² = b² + c² - 2bccos∠A

= 8² + 5² - 2.8.5.cos120^o

$=64+25+80\frac{1}{2}=129$ $=64+25+80\frac{1}{2}=129$

$=>a=\sqrt{129}=11,36\ \left(cm\right)$ $=>a=\sqrt{129}=11,36\ \left(cm\right)$

Ta có:

$\frac{a}{sin\hat{A} } = \frac{b}{sin\hat{B} }\Rightarrow sin\hat{B}= \frac{b.sin\hat{A}}{a} =\frac{8.\frac{\sqrt{3} }{2} }{11,36} =\frac{4.\sqrt{3} }{11,36} =0,61$ $\frac{a}{sin\hat{A} } = \frac{b}{sin\hat{B} }\Rightarrow sin\hat{B}= \frac{b.sin\hat{A}}{a} =\frac{8.\frac{\sqrt{3} }{2} }{11,36} =\frac{4.\sqrt{3} }{11,36} =0,61$

=> ∠B = 37^o34'

=> ∠C = 180^o - (∠A + ∠B)

= 180^o - (120^o + 37^o34') = 22^o26'

Bài 4 trang 59 SGK Hình học 10

Tính diện tích S của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.

Lời giải:

Ta có:

$p=\frac{a+b+c}{2}=\frac{7+9+12}{2}=14$ $p=\frac{a+b+c}{2}=\frac{7+9+12}{2}=14$

$p-a=7$

$p-b=5$

$p-c=2$

Vậy $S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{14.7.5.2}=7.2.\sqrt{5}=14\sqrt{5}=31,3\left(đvdt\right)$ $S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{14.7.5.2}=7.2.\sqrt{5}=14\sqrt{5}=31,3\left(đvdt\right)$

Bài 5 trang 59 SGK Hình học 10

Cho tam giác ABC có ∠A = 120^o. Tính cạnh BC, cho biết cạnh AC = m và cạnh AB = n.

Lời giải:

Ta có: BC² = AC² + AB² - 2.AB.AC.cos∠A

= m² + n² - 2.m.n.cos120^o

= m² + n² + mn

$BC=\sqrt{m^2+n^2+m.n}$ $BC=\sqrt{m^2+n^2+m.n}$

Bài 6 trang 59 SGK Hình học 10

Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.

a) Tam giác đó có góc tù không?

b) Tính độ dài trung tuyến MA của tam giác ABC đó.

Lời giải:

a) Ta có:

$cos\hat{C} = \frac{a^2 + b^2 - c^2}{2ab} = \frac{8^2+10^2-13^2}{2.8.10}$ $cos\hat{C} = \frac{a^2 + b^2 - c^2}{2ab} = \frac{8^2+10^2-13^2}{2.8.10}$ $\frac{ }{ }\sim-0,031$ $\frac{ }{ }\sim-0,031$

Vậy $\angle C\ =\ 91^{o} 47^{$ $\angle C\ =\ 91^{o} 47^{'}$

Vậy trong tam giác có góc C là góc tù.

b)

Ta có:

$AM^2=\frac{2\left(AC^2+AB^2\right)-BC^2}{4}=\frac{2\left(10^2+13^2\right)-8^2}{4}=118,5$ $AM^2=\frac{2\left(AC^2+AB^2\right)-BC^2}{4}=\frac{2\left(10^2+13^2\right)-8^2}{4}=118,5$

Vậy $AM\ =\ \sqrt{118,5}=10,89$ $AM\ =\ \sqrt{118,5}=10,89$

Bài 7 trang 59 SGK Hình học 10

Tính góc lớn nhất của tam giác ABC biết:

a) Các cạnh a = 3cm, b = 4cm và c = 6cm;

b) Các cạnh a = 40cm, b = 13cm, c = 37cm.

Lời giải:

a) Cạnh c = 6cm lớn nhất suy ra là góc C là góc lớn nhất.

$cos\hat{C} = \frac{a^2 + b^2 - c^2}{2ab} = \frac{3^2+4^2-6^2}{2.3.4} =\frac{-11}{24} =-0,458$ $cos\hat{C} = \frac{a^2 + b^2 - c^2}{2ab} = \frac{3^2+4^2-6^2}{2.3.4} =\frac{-11}{24} =-0,458$

Vậy $\angle C=117^o16$ $\angle C=117^o16'$

b, Cạnh a = 40cm lớn nhất suy ra góc A là góc lớn nhất.

$cos\hat{A} = \frac{b^2 + c^2 - a^2}{2bc} = \frac{13^2+37^2-40^2}{2.13.37} =-0,0644$ $cos\hat{A} = \frac{b^2 + c^2 - a^2}{2bc} = \frac{13^2+37^2-40^2}{2.13.37} =-0,0644$

Vậy $\angle A=93^o41$ $\angle A=93^o41'$

Bài 8 trang 59 SGK Hình học 10

Cho tam giác ABC biết cạnh a = 137,5cm, ∠B = 83^o và ∠C = 57^o. Tính góc A, bán kính R của đường tròn ngoại tiếp, cạnh b và c của tam giác.

Lời giải:

Ta có: ∠A = 180^o - (∠B + ∠C) = 180^o - (83^o + 57^o) = 40^o

Áp dụng định lí sin ta có:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$ $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$

Từ đó suy ra:

$\Rightarrow\ R=\frac{a}{2\sin A}=\frac{137,5}{2\sin40^o}=106,96cm$ $\Rightarrow\ R=\frac{a}{2\sin A}=\frac{137,5}{2\sin40^o}=106,96cm$

$=>b=2R.\sin B=2.106,96.\sin83^o=212,33cm$ $=>b=2R.\sin B=2.106,96.\sin83^o=212,33cm$

$=>c=2R.\sin C=2.106,96.\sin57^o=179,41cm$ $=>c=2R.\sin C=2.106,96.\sin57^o=179,41cm$

Bài 9 trang 59 SGK Hình học 10

Cho hình bình hành ABCD có AB = a, BC = b, BD = m, AC = n. Chứng minh rằng: m² + n² = 2(a² + b²).

Lời giải:

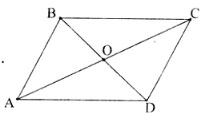
Các hệ thức lượng trong tam giác và giải tam giác

Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và BD, đồng thời BO là trung tuyến của ΔABC.

Suy ra:

$BO^2=\frac{2\left(AB^2+BC^2\right)-AC^2}{4}=\frac{2\left(a^2+b^2\right)-n^2}{4}$ $BO^2=\frac{2\left(AB^2+BC^2\right)-AC^2}{4}=\frac{2\left(a^2+b^2\right)-n^2}{4}$

$BO=\frac{1}{2}BD;\ nên\ BO^2=\frac{1}{4}BD^2=\frac{m^2}{4}$ $BO=\frac{1}{2}BD;\ nên\ BO^2=\frac{1}{4}BD^2=\frac{m^2}{4}$

$Nên\ \frac{m^2}{4}=\frac{2\left(a^2+b^2\right)-n^2}{4}$ $Nên\ \frac{m^2}{4}=\frac{2\left(a^2+b^2\right)-n^2}{4}$

⇔ m² + n² = 2(a² + b²) (đpcm)

Bài 10 trang 60 SGK Hình học 10

Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ra nhìn chiều cao AB của tháp dưới các góc ∠BPA = 35^o và ∠BQA = 48^o. Tính chiều cao của tháp.

Lời giải:

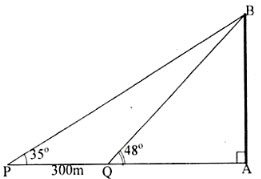
Các hệ thức lượng trong tam giác và giải tam giác

ΔAPB vuông tại A có ∠APB = 35^o

=> AP = ABcot35^o (1)

ΔAQB vuông tại A có ∠AQB = 35^o

=> AQ = ABcot48^o (2)

Từ (1) và (2) suy ra:

PQ = AP - AQ = AB(cot35^o - cot48^o)

$\Rightarrow\ AB=\frac{300}{\cot35^o-\cot48^o}=586,457m$ $\Rightarrow\ AB=\frac{300}{\cot35^o-\cot48^o}=586,457m$

Bài 11 trang 60 SGK Hình học 10

Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế (hình bên). Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm A₁, B₁ cùng thẳng hàng với C₁ thuộc chiều cao CD của tháp. Người ta đo được ∠DA₁C₁ = 49^o và ∠DB₁C₁ = 35^o. Tính chiều cao CD của tháp đó.

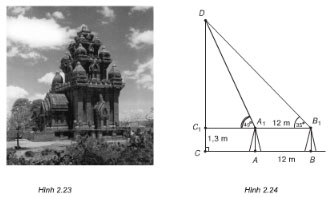
Các hệ thức lượng trong tam giác và giải tam giác

Lời giải:

Ta có: A₁B₁ = AB = 12 m

Xét ΔDC₁A₁ có: C₁A₁ = C₁D.cot49^o

Xét ΔDC₁B₁ có: C₁B₁ = C₁D.cot35^o

Mà A₁B₁ = C₁B₁ - C₁A₁ = C₁D.cot35^o - C₁D.cot49^o

= C₁D.(cot35^o - cot49^o)

$\Rightarrow\ C_1D=\frac{A_1B_1}{\cot35^o-\cot49^o}=\frac{12}{\cot35^o-\cot49^o}=21,47m$ $\Rightarrow\ C_1D=\frac{A_1B_1}{\cot35^o-\cot49^o}=\frac{12}{\cot35^o-\cot49^o}=21,47m$

=> Chiều cao CD của tháp là:

$CD=1,3+21,47=22,77m$

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải bài tập Hình học 10 bài 3: Các hệ thức lượng trong tam giác và giải tam giác để bạn đọc cùng tham khảo. Mời bạn đọc cùng tham khảo thêm tài liệu học tập các môn Hóa học lớp 10, Vật lý lớp 10...

Chia sẻ, đánh giá bài viết

1

8.130

Bài trước

Bài sau