VnDoc.com

Công thức Heron, cách tính diện tích tam giác bằng công thức Heron

Công thức Heron lớp 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Phân loại: Tài liệu Tính phí

Công thức Hê Rông (Heron)

Công thức Heron
- Cách chứng minh công thức Heron
Bài tập áp dụng công thức Heron

Công thức Heron là một trong những kiến thức trọng tâm trong chương trình Toán lớp 10, giúp học sinh tính nhanh diện tích tam giác khi biết độ dài ba cạnh mà không cần phải xác định chiều cao. Đây là công cụ rất hữu ích trong nhiều bài toán hình học, đặc biệt trong các đề thi kiểm tra và ôn thi học kỳ. Bài viết này sẽ giới thiệu chi tiết công thức Heron, hướng dẫn cách áp dụng đúng chuẩn và dễ hiểu để tính diện tích tam giác, kèm theo các ví dụ minh họa cụ thể giúp bạn nắm chắc kiến thức và vận dụng hiệu quả.

Công thức Heron là công thức tính diện tích của một tam giác theo độ dài 3 cạnh. Đây là công thức mang tên nhà toán học Heron của Alexandria.

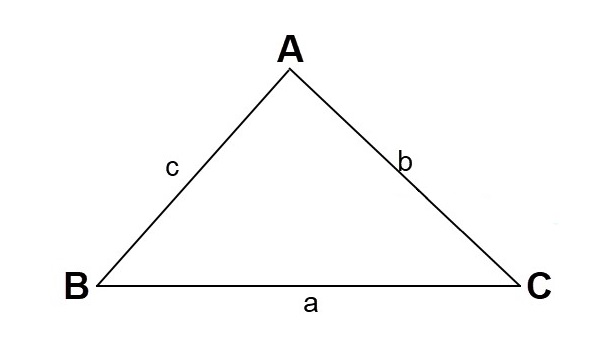
Công thức Heron, cách tính diện tích tam giác bằng công thức Heron

Công thức Heron

Gọi S là diện tích và độ dài 3 cạnh tam giác lần lượt là a, b và c

$S=\sqrt{p(p-a)(p-b)(p-c)}$ $S=\sqrt{p(p-a)(p-b)(p-c)}$

Với p là nửa chu vi của tam giác $p=\frac{a+b+c}{2}$ $p=\frac{a+b+c}{2}$.

Công thức Heron còn có thể được viết lại bằng:

$\begin{aligned} S=& \frac{\sqrt{(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}{4} \\ S &=\frac{\sqrt{2\left(a^{2} b^{2}+a^{2} c^{2}+b^{2} c^{2}\right)-\left(a^{4}+b^{4}+c^{4}\right)}}{4} \\ & S=\frac{\sqrt{\left(a^{2}+b^{2}+c^{2}\right)^{2}-2\left(a^{4}+b^{4}+c^{4}\right)}}{4} \end{aligned}$ $\begin{aligned} S=& \frac{\sqrt{(a+b+c)(a+b-c)(b+c-a)(c+a-b)}}{4} \\ S &=\frac{\sqrt{2\left(a^{2} b^{2}+a^{2} c^{2}+b^{2} c^{2}\right)-\left(a^{4}+b^{4}+c^{4}\right)}}{4} \\ & S=\frac{\sqrt{\left(a^{2}+b^{2}+c^{2}\right)^{2}-2\left(a^{4}+b^{4}+c^{4}\right)}}{4} \end{aligned}$

Cách chứng minh công thức Heron

Cách chứng minh này sử dụng đại số và lượng giác

Gọi a, b, c lần lượt là 3 cạnh của tam giác và A, B, C lần lượt là các góc đối diện của các cạnh. Theo hệ quả định lý cosin, ta có:

$\cos (C)=\frac{a^{2}+b^{2}-c^{2}}{2 a b}$ $\cos (C)=\frac{a^{2}+b^{2}-c^{2}}{2 a b}$

Từ đó:

$\sin (C)=\sqrt{1-\cos ^{2}(C)}=\frac{\sqrt{4 a^{2} b^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}}}{2 a b}$ $\sin (C)=\sqrt{1-\cos ^{2}(C)}=\frac{\sqrt{4 a^{2} b^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}}}{2 a b}$

Dựa vào đường cao và sin của góc C. Ta có công thức tính diện tích tam giác ABC:

$\begin{aligned} S &=\frac{1}{2} a b \sin (C) \\ &=\frac{1}{4} \sqrt{4 a^{2} b^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}} \\ &=\frac{1}{4} \sqrt{\left(2 a b-\left(a^{2}+b^{2}-c^{2}\right)\right)\left(2 a b+\left(a^{2}+b^{2}-c^{2}\right)\right)} \\ &=\frac{1}{4} \sqrt{\left(c^{2}-(a-b)^{2}\right)\left((a+b)^{2}-c^{2}\right)} \end{aligned}$ $\begin{aligned} S &=\frac{1}{2} a b \sin (C) \\ &=\frac{1}{4} \sqrt{4 a^{2} b^{2}-\left(a^{2}+b^{2}-c^{2}\right)^{2}} \\ &=\frac{1}{4} \sqrt{\left(2 a b-\left(a^{2}+b^{2}-c^{2}\right)\right)\left(2 a b+\left(a^{2}+b^{2}-c^{2}\right)\right)} \\ &=\frac{1}{4} \sqrt{\left(c^{2}-(a-b)^{2}\right)\left((a+b)^{2}-c^{2}\right)} \end{aligned}$

$\begin{array}{l} =\frac{1}{4} \sqrt{(c-(a-b))((c+(a-b))((a+b)-c))((a+b)+c)} \\ =\sqrt{p(p-a)(p-b)(p-c)} \end{array}$ $\begin{array}{l} =\frac{1}{4} \sqrt{(c-(a-b))((c+(a-b))((a+b)-c))((a+b)+c)} \\ =\sqrt{p(p-a)(p-b)(p-c)} \end{array}$

Vậy nếu các bạn muốn tính diện tích tam giác với ba cạnh a, b, c thì các bạn cần tính nửa chu vi của tam giác với công thức:

$p=\frac{a+b+c}{2}$ $p=\frac{a+b+c}{2}$

Sau đó áp dụng công thức tính diện tích Heron để tính diện tích tam giác:

$S=\sqrt{p(p-a)(p-b)(p-c)}$ $S=\sqrt{p(p-a)(p-b)(p-c)}$.

Bài tập áp dụng công thức Heron

Ví dụ 1: Cho tam giác ABC có độ dài ba cạnh là $AB=52, AC=56,BC=60$. Hãy tính bán kính đường tròn ngoại tiếp tam giác ABC?

Hướng dẫn giải

Ta có: $p = \frac{52 + 56 + 60}{2} = 84$ $p = \frac{52 + 56 + 60}{2} = 84$.

Áp dụng hệ thức Hê - rông ta có:

$S = \sqrt{84 \cdot (84 - 52) \cdot (84 - 56) \cdot (84 - 60)} = 1344$ $S = \sqrt{84 \cdot (84 - 52) \cdot (84 - 56) \cdot (84 - 60)} = 1344$.

Mặt khác $S = \frac{abc}{4R} \Rightarrow R = \frac{abc}{4S\ } = \frac{52.56.60}{4.1344} = 32.5$ $S = \frac{abc}{4R} \Rightarrow R = \frac{abc}{4S\ } = \frac{52.56.60}{4.1344} = 32.5$

Ví dụ 2: Tính diện tích tam giác có ba cạnh lần lượt là $\sqrt{3},\sqrt{2}$ $\sqrt{3},\sqrt{2}$ và 1?

Hướng dẫn giải

Nửa chu vi của tam giác là:

$p = \frac{{a + b + c}}{2} = \frac{{\sqrt 3 + \sqrt 2 + 1}}{2}$ $p = \frac{{a + b + c}}{2} = \frac{{\sqrt 3 + \sqrt 2 + 1}}{2}$

Áp dụng công thức Herong ta có:

$S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$ $S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

$S = \sqrt {p\left( {p - \sqrt 3 } \right)\left( {p - \sqrt 2 } \right)\left( {p - 1} \right)}$ $S = \sqrt {p\left( {p - \sqrt 3 } \right)\left( {p - \sqrt 2 } \right)\left( {p - 1} \right)}$

$S = \frac{{\sqrt 2 }}{2}$ $S = \frac{{\sqrt 2 }}{2}$

Ví dụ 3: Cho tam giác ABC có a = 13; b = 14; c = 15.

a. Tính sin A.

b. Tính diện tích S của tam giác bằng hai cách khác nhau.

Hướng dẫn giải

a. Áp dụng định lí cosin cho tam giác ABC ta có:

$\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$ $\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$ $= \frac{{{{14}^2} + {{15}^2} - {{13}^2}}}{{2.14.15}} = 0,6$ $= \frac{{{{14}^2} + {{15}^2} - {{13}^2}}}{{2.14.15}} = 0,6$

Do đó:

$\sin A = \sqrt {1 - {{\cos }^2}A} = \sqrt {1 - 0,{6^2}} = 0,8$ $\sin A = \sqrt {1 - {{\cos }^2}A} = \sqrt {1 - 0,{6^2}} = 0,8$

b. Cách 1: Diện tích tam giác ABC là:

$S = \frac{1}{2}b.c.\sin A = 84$ $S = \frac{1}{2}b.c.\sin A = 84$(đơn vị diện tích).

Cách 2: Áp dụng côn thức Heron, ta cũng có thể tính diện tích tam giác ABC như sau:

Tam giác ABC có nửa chu vi là:

$p = \frac{{a + b + c}}{2} = \frac{{13 + 14 + 15}}{2} = 21$ $p = \frac{{a + b + c}}{2} = \frac{{13 + 14 + 15}}{2} = 21$

Khi đó, diện tích tam giác ABC là:

$S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$ $S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}$

$S = \sqrt {21.\left( {21 - 13} \right)\left( {21 - 14} \right)\left( {21 - 15} \right)} = 84$ $S = \sqrt {21.\left( {21 - 13} \right)\left( {21 - 14} \right)\left( {21 - 15} \right)} = 84$ (đơn vị diện tích).

Ví dụ 4: Cho tam giác $ABC$ biết $AB = 6,\ \ BC = 8,\ \ CA = 10$ $AB = 6,\ \ BC = 8,\ \ CA = 10$. Diện tích của tam giác $\Delta ABC$ $\Delta ABC$ bằng:

A. $48.$ B. $24$. C. $6$. D. $8$.

Hướng dẫn giải

Chọn B

Ta có: $p = \frac{AB + AC + BC}{2} = \frac{6 + 8 + 10}{2} = 12$ $p = \frac{AB + AC + BC}{2} = \frac{6 + 8 + 10}{2} = 12$.

Vậy diện tích tam giác $ABC$ là:

$S = \sqrt{p(p - AB)(p - AC)(p - BC)}$ $S = \sqrt{p(p - AB)(p - AC)(p - BC)}$

$= \sqrt{12(12 - 6)(12 - 8)(12 - 10)} = 24$ $= \sqrt{12(12 - 6)(12 - 8)(12 - 10)} = 24$.

Ví dụ 5: Tính diện tích tam giác $ABC$ biết $AB = 3,\ \ BC = 5,\ \ CA = 6$ $AB = 3,\ \ BC = 5,\ \ CA = 6$.

A. $2\sqrt{14}$ $2\sqrt{14}$. B. $\sqrt{48}$ $\sqrt{48}$. C. $6$. D. $8$.

Hướng dẫn giải

Ta có: $p = \frac{AB + AC + BC}{2} = \frac{3 + 5 + 6}{2} = 7$ $p = \frac{AB + AC + BC}{2} = \frac{3 + 5 + 6}{2} = 7$

Vậy diện tích tam giác $ABC$ là

$S = \sqrt{p(p - AB)(p - AC)(p - BC)}$ $S = \sqrt{p(p - AB)(p - AC)(p - BC)}$

$= \sqrt{7(7 - 3)(7 - 6)(7 - 5)} = \sqrt{56} = 2\sqrt{14}$ $= \sqrt{7(7 - 3)(7 - 6)(7 - 5)} = \sqrt{56} = 2\sqrt{14}$

Ví dụ 6: Tính bán kính đường tròn ngoại tiếp tam giác ABC, biết rằng độ dài các cạnh AB; BC; AC lần lượt là 5; 7; 8.

Hướng dẫn giải

Nửa chu vi $\Delta ABC$ $\Delta ABC$ là: $p = \frac{AB + BC + AC}{2} = 10$ $p = \frac{AB + BC + AC}{2} = 10$.

Diện tích $\Delta ABC$ $\Delta ABC$ là:

$S = \sqrt{p(p - AB)(p - BC)(p - AC)}$ $S = \sqrt{p(p - AB)(p - BC)(p - AC)}$

$= \sqrt{10(10 - 5)(10 - 7)(10 - 8)} = 10\sqrt{3}$ $= \sqrt{10(10 - 5)(10 - 7)(10 - 8)} = 10\sqrt{3}$

Ta có $S = pr \Rightarrow r = \frac{S}{p} = \frac{10\sqrt{3}}{\sqrt{3}} = \sqrt{3}$ $S = pr \Rightarrow r = \frac{S}{p} = \frac{10\sqrt{3}}{\sqrt{3}} = \sqrt{3}$.

Ví dụ 7: Cho tam giác $ABC$ có $AB = 6cm$, $AC = BC = 5cm$. Tính bán kính của đường tròn ngoại tiếp tam giác $ABC$?

A. $\frac{25}{8}.$ $\frac{25}{8}.$ B. $\frac{5}{2}.$ $\frac{5}{2}.$ C. $3.$ D. $\frac{7}{2}.$ $\frac{7}{2}.$

Hướng dẫn giải

Theo bài ra: có $AB = 6cm$, $AC = BC = 5cm$ suy ra:

$p = \frac{6 + 5 + 5}{2} = 8.$ $p = \frac{6 + 5 + 5}{2} = 8.$

$S_{ABC} = \sqrt{p(p - a)(p - b)(p - c)}$ $S_{ABC} = \sqrt{p(p - a)(p - b)(p - c)}$

$= \sqrt{8(8 - 5)(8 - 5)(8 - 6)} = 12$ $= \sqrt{8(8 - 5)(8 - 5)(8 - 6)} = 12$.

Mà $S = \frac{abc}{4R} \Rightarrow R = \frac{abc}{4S} = \frac{5.5.6}{4.12} = \frac{25}{8}$ $S = \frac{abc}{4R} \Rightarrow R = \frac{abc}{4S} = \frac{5.5.6}{4.12} = \frac{25}{8}$.

Ví dụ 8: Tính bán kính đường tròn ngoại tiếp tam giác ABC, biết rằng độ dài các cạnh AB, BC, CA lần lượt là 3; 5; 6.

Hướng dẫn giải

Ta có: $p = \frac{AB + AC + BC}{2} = \frac{3 + 5 + 6}{2} = 7$ $p = \frac{AB + AC + BC}{2} = \frac{3 + 5 + 6}{2} = 7$.

Diện tích tam giác $ABC$ là:

$S = \sqrt{p(p - AB)(p - AC)(p - BC)}$ $S = \sqrt{p(p - AB)(p - AC)(p - BC)}$

$= \sqrt{7(7 - 3)(7 - 6)(7 - 5)} = \sqrt{56}$ $= \sqrt{7(7 - 3)(7 - 6)(7 - 5)} = \sqrt{56}$.

Bán kính đường tròn ngoại tiếp tam giác ABC là.

$S = \frac{a.b.c}{4R} \Rightarrow R = \frac{a.b.c}{4.S} = \frac{3.5.6}{4.\sqrt{56}} = \frac{45\sqrt{14}}{56}$ $S = \frac{a.b.c}{4R} \Rightarrow R = \frac{a.b.c}{4.S} = \frac{3.5.6}{4.\sqrt{56}} = \frac{45\sqrt{14}}{56}$.

Trắc nghiệm Công thức Heron có đáp án chi tiết

Câu 1: Cho tam giác $ABC$ có $a = 4,\ \ b = 6,\ \ c = 8$ $a = 4,\ \ b = 6,\ \ c = 8$. Khi đó diện tích của tam giác là:

A. $3\sqrt{15}$ $3\sqrt{15}$. B. $105$. C. $\frac{2}{3}\sqrt{15}$ $\frac{2}{3}\sqrt{15}$. D. $9\sqrt{15}$ $9\sqrt{15}$.

Câu 2: Cho tam giác $ABC$ có $AB = 3,BC = 5,CA = 6$. Tính bán kính đường tròn ngoại tiếp tam giác.

A. $\frac{45\sqrt{14}}{56}$ $\frac{45\sqrt{14}}{56}$. B. $\frac{54\sqrt{14}}{56}$ $\frac{54\sqrt{14}}{56}$. C. $\frac{45\sqrt{14}}{57}$ $\frac{45\sqrt{14}}{57}$. D. $\frac{45\sqrt{14}}{65}$ $\frac{45\sqrt{14}}{65}$.

Câu 3: Một tam giác có ba cạnh là $52,56,60$. Bán kính đường tròn ngoại tiếp là:

A. $\frac{65}{8}.$ $\frac{65}{8}.$ B. $40.$ C. $32,5.$ D. $\frac{65}{4}.$ $\frac{65}{4}.$

Câu 4: Cho tam giác $ABC$ có $a = 4,b = 6,c = 8$. Khi đó diện tích của tam giác là:

A. $9\sqrt{15}.$ $9\sqrt{15}.$ B. $3\sqrt{15}.$ $3\sqrt{15}.$ C. $105.$ D. $\frac{2}{3}\sqrt{15}.$ $\frac{2}{3}\sqrt{15}.$

Câu 5: Tam giác $ABC$ có $BC = 2\sqrt{3},\ AC = 2AB$ $BC = 2\sqrt{3},\ AC = 2AB$ và độ dài đường cao $AH = 2$. Tính độ dài cạnh $AB$.

A. $AB = 2$. B. $AB = \frac{2\sqrt{3}}{3}$ $AB = \frac{2\sqrt{3}}{3}$.

C. $AB = 2$ hoặc $AB = \frac{2\sqrt{21}}{3}$ $AB = \frac{2\sqrt{21}}{3}$. D. $AB = 2$ hoặc $AB = \frac{2\sqrt{3}}{3}$ $AB = \frac{2\sqrt{3}}{3}$.

Câu 6: Một tam giác có ba cạnh là $13,14,15$. Diện tích tam giác bằng bao nhiêu?

A. $84\ .$ $84\ .$ B. $\sqrt{84}\ .$ $\sqrt{84}\ .$ C. $42\ .$ $42\ .$ D. $\sqrt{168}\ .$ $\sqrt{168}\ .$

Câu 7: Tam giác với ba cạnh là $3,4,5.$ Có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu?

A. $1.$ B. $\sqrt{2}.$ $\sqrt{2}.$ C. $\sqrt{3}.$ $\sqrt{3}.$ D. $2.$

Câu 8. Cho tam giác $ABC$ biết $AB = 6,\ \ BC = 8,\ \ CA = 10$ $AB = 6,\ \ BC = 8,\ \ CA = 10$. Diện tích của tam giác $\Delta ABC$ $\Delta ABC$ bằng:

A. $48.$ B. $24$. C. $6$. D. $8$.

Câu 9: Tính diện tích tam giác $ABC$ biết $AB = 3,\ \ BC = 5,\ \ CA = 6$ $AB = 3,\ \ BC = 5,\ \ CA = 6$.

A. $2\sqrt{14}$ $2\sqrt{14}$. B. $\sqrt{48}$ $\sqrt{48}$. C. $6$. D. $8$.

Câu 10: Cho tam giác $ABC$ có $AB = 5;BC = 7;AC = 8$. Bán kính đường tròn nội tiếp tam giác $ABC$ bằng

A. $r = \sqrt{3}.$ $r = \sqrt{3}.$ B. $r = 3\sqrt{13}.$ $r = 3\sqrt{13}.$ C. $r = \frac{1}{3}.$ $r = \frac{1}{3}.$ D. $r = 3.$

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

-------------------------------------------------------------

Hiểu và vận dụng thành thạo công thức Heron tính diện tích tam giác không chỉ giúp bạn giải nhanh các bài toán hình học lớp 10 mà còn là nền tảng để tiếp cận các bài toán hình học phức tạp hơn trong các năm học tiếp theo. Để nâng cao kỹ năng, bạn nên luyện tập thêm nhiều dạng bài tập thực tế và các bài toán vận dụng công thức trong các trường hợp đặc biệt như tam giác cân, tam giác vuông hay tam giác tù.

Ngoài ra, đừng quên theo dõi VnDoc.com để cập nhật các bài viết bổ ích liên quan đến hình học lớp 10, mẹo giải toán nhanh, và bộ đề luyện thi hiệu quả, giúp bạn tự tin chinh phục các kỳ thi quan trọng. Hãy biến toán học trở thành người bạn đồng hành thú vị trên con đường học tập của bạn!

Bài tập áp dụng công thức Heron

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Su kem

6

15.764

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!