Lập phương trình chính tắc Hypebol (cách giải chi tiết)
Viết phương trình chính tắc của Hypebol - có đáp án
Hypebol là một trong những dạng đường conic quan trọng của chương trình Toán 10, đặc biệt hữu ích trong các bài toán hình học giải tích. Bài viết này sẽ hướng dẫn bạn cách lập phương trình chính tắc của hypebol dựa vào các dữ kiện cơ bản như tâm, trục, tiêu điểm và độ lệch tâm. Đồng thời, bạn sẽ được tiếp cận phương pháp giải chi tiết, kèm theo hệ thống bài tập có đáp án giúp bạn dễ dàng ôn luyện và nắm chắc kiến thức.
A. Cách viết phương trình Hypebol
Hypebol
Trên mặt phẳng, nếu hai thiết bị đặt tại các vị trí 
\(F_{1}\),\(F_{2}\) nhận được một tín hiệu âm thanh cùng lúc thì vị trí phát ra tín hiệu cách đều hai điểm \(F_{1}\),\(F_{2}\), và do đó, nằm trên đường trung trực của đoạn thẳng \(F_{1}F_{2}\).
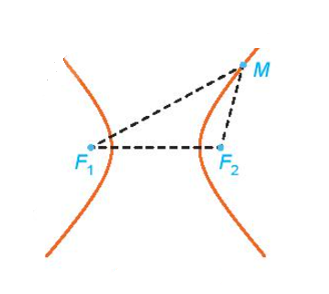
Cho hai điểm phân biệt cố định \(F_{1}\), \(F_{2}\). Đặt \(F_{1}F_{2} = 2c\). Cho số thực dương \(a\) nhỏ hơn \(c\). Tập hợp các điểm \(M\) sao cho \(\left| MF_{1} - MF_{2} \right| = 2a\) được gọi là đường hypebol. Hai điểm \(F_{1}\), \(F_{2}\) được gọi là hai tiêu điểm và \(F_{1}F_{2} = 2c\) được gọi là tiêu cự của hypebol đó.
Phương trình chính tắc của Hypebol
Trong mặt phẳng tọa độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn thẳng nối hai tiêu điểm đó thì có phương trình \(\frac{x^{2}}{a^{2}} -
\frac{y^{2}}{b^{2}} = 1\), với \(a,b
> 0\).
Ngược lại, mỗi phương trình có dạng \((4)\) đều là phương trình của hypebol có hai tiêu điểm \(F_{1}\left( - \sqrt{a^{2} +
b^{2}};0 \right)\), \(F_{2}\left(
\sqrt{a^{2} + b^{2}};0 \right)\), tiêu cự \(2x = 2\sqrt{a^{2} + b^{2}}\) và giá trị tuyệt đối của hiệu các khoảng cách từ mỗi điểm thuộc hypebol đến hai tiêu điểm bằng \(2a\).
Phương trình được gọi là phương trình chính tắc của hypebol tương ứng.
B. Ví dụ minh họa viết phương trình chính tắc của Hypebol
Ví dụ 1: Lập phương trình chính tắc của hypebol biết:
a) Nửa trục thực bằng \(4\), nửa tiêu cự bằng \(10\).
b) Tiêu cự bằng một tiệm cận là \(y =
\frac{2}{3}x\).
c) Tâm sai \(e = \sqrt{5}\) và hypebol qua điểm \(M\left( \sqrt{10};6
\right)\).
Hướng dẫn giải
a) Ta có: \(a = 4,c = 5\), nên \(b^{2} = c^{2} - a^{2} = 9\)
Vậy phương trình của hypebol là: \(\frac{x^{2}}{16} - \frac{y^{2}}{9} =
1\)
b) Ta có: \(c = \sqrt{13}\) và \(\frac{b}{a} = \frac{2}{3} \Rightarrow
\frac{b^{2}}{a^{2}} = \frac{4}{9} \Rightarrow \frac{b^{2} +
a^{2}}{a^{2}} = \frac{13}{9}\)
Ta lại có \(b^{2} + a^{2} = c^{2} =
13\) nên \(a^{2} = 9,\ \ b^{2} =
4\)
Do đó phương trình của hypebol là: \(\frac{x^{2}}{9} - \frac{y^{2}}{4} = 1\)
c) Gọi phương trình hypebol là \(\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} =
1\)
Và \(M\left( \sqrt{10};6 \right) \in (H)
\Rightarrow \frac{10}{a^{2}} - \frac{36}{b^{2}} = 1(1)\)
Ta có:\(e = \sqrt{5} \Rightarrow
\frac{c}{a} = \sqrt{5}\) hay \(\frac{c^{2}}{a^{2}} = 5 \Rightarrow \frac{c^{2} -
a^{2}}{a^{2}} = 4 \Rightarrow \frac{b^{2}}{a^{2}} = 4(2)\)
Từ \((1),(2) \Rightarrow a^{2} = 1,\ \
b^{2} = 4\).
Do đó, phương trình hypebol là: \(\frac{x^{2}}{1} - \frac{y^{2}}{4} =
1\).
Ví dụ 2: Cho hypebol \(\frac{x^{2}}{16} -
\frac{y^{2}}{9} = 1\ \ \ \ (H)\)
a) Tìm độ dài trục ảo, trục thực, tâm sai, tiêu điểm \(F_{1},F_{2}\) của hypebol, vẽ hypebol \((H)\)
b) Tìm trên \((H)\) những điểm \(M\) sao cho \(MF_{1}\bot MF_{2}\).
Hướng dẫn giải
Hình vẽ minh họa:
a) Ta có \((H):\frac{x^{2}}{16} -
\frac{y^{2}}{9} = 1\)
\(\Rightarrow \ \ \ \ a^{2} = 16,\ \ b^{2}
= 9\)
\(\Rightarrow \ \ \ \ c^{2} =
25\)
Vậy độ dài trục ảo là \(2b = 6\), độ dài trục thực là \(2a = 8\)
Tâm sai \(e = \frac{a}{c} = \frac{5}{4}
> 1\),\(F_{1}( - 5;0),\ \ \ \
F_{2}(5;0)\).
b) Gọi \(M(x,y) \in (H)\) sao cho \(MF_{1}\bot MF_{2} \Rightarrow
\widehat{F_{1}MF_{2}} = 90^{0}\)
Vậy \(M\) nằm trên đường tròn đường kính \(F_{1}F_{2} = 10\) có phương trình là \(x^{2} + y^{2} = 25\).
Do đó tọa độ của \(M\) là nghiệm của hệ phương trình:
\(\left\{ \begin{matrix}
\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1 \\
x^{2} + y^{2} = 25
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x = \pm \frac{4\sqrt{34}}{5} \\
y = \pm \frac{9}{5}
\end{matrix} \right.\)
Vậy ta có \(4\) điểm \(M\) là:
\(M_{1}\left(
\frac{4\sqrt{34}}{5};\frac{9}{5} \right);M_{2}\left(
\frac{4\sqrt{34}}{5}; - \frac{9}{5} \right);M_{3}\left( -
\frac{4\sqrt{34}}{5};\frac{9}{5} \right);M_{4}\left( -
\frac{4\sqrt{34}}{5}; - \frac{9}{5} \right)\).
C. Bài tập vận dụng lập phương trình Hypebol
Bài tập 1. Cho hypebol: \(\frac{x^{2}}{4} -
y^{2} = 1\ \ \ (H)\)
a) Định tiêu điểm. Viết phương trình các tiệm cận.
b) Cho \(M\left( x_{0};y_{0} \right) \in
(H)\). Tính tích số khoảng cách từ \(M\)đến các tiệm cận.
Bài tập 2: a) Lập phương trình chính tắc của hypebol với tổng hai bán trục là \(a + b = 7\) hai tiệm cận \(y = \pm \frac{3}{4}x\)
b) Tính độ dài hai bán trục. Vẽ \((H)\).
c) Lập phương trình các tiếp tuyến của \((H)\), biết rằng tiếp tuyến song song \(d:5x - 4y + 10 = 0\).
Toàn bộ tài liệu nằm trong File tải, mời bạn đọc tải tài liệu tham khảo đầy đủ!
--------------------------------------
Hy vọng với những kiến thức và phương pháp trình bày trong bài viết, bạn đã hiểu rõ cách lập phương trình chính tắc của hypebol và biết cách áp dụng vào bài tập Toán 10 một cách tự tin. Hãy luyện tập thêm các ví dụ minh họa và thử sức với nhiều dạng đề để tăng kỹ năng giải nhanh – chính xác. Đừng quên theo dõi thêm các chủ đề conic khác để hoàn thiện nền tảng hình học giải tích của bạn.
