VnDoc.com

Phương trình Elip trong mặt phẳng tọa độ Oxy

Toán lớp 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Toán 10: Phương trình Elip

Phương trình elip là một trong những nội dung trọng tâm của chương trình Toán lớp 10, đặc biệt quan trọng trong chủ đề hình học giải tích. Trong bài viết này, chúng ta sẽ cùng tìm hiểu định nghĩa elip, các dạng phương trình elip trong mặt phẳng tọa độ Oxy và cách vận dụng vào giải bài tập. Với cách trình bày trực quan, dễ hiểu, bài viết sẽ giúp bạn nắm vững kiến thức và áp dụng hiệu quả trong các dạng toán liên quan.

I. Kiến thức cần nhớ

1) Elip

Cho hai điểm cố định $F_{1},\ \ F_{2}$ $F_{1},\ \ F_{2}$ với $F_{1}F_{2} = 2c(c > 0)$ $F_{1}F_{2} = 2c(c > 0)$ và hằng số $a > c.$

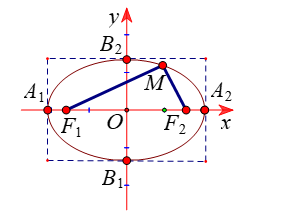
Elip $(E)$ là tập hợp các điểm $M$ thỏa mãn $MF_{1} + MF_{2} = 2a$ $MF_{1} + MF_{2} = 2a$.

Các điểm $F_{1},F_{2}$ $F_{1},F_{2}$ là tiêu điểm của $(E).$

Khoảng cách $F_{1}F_{2} = 2c$ $F_{1}F_{2} = 2c$ là tiêu cự của $(E).$ $MF_{1},\ \ MF_{2}$ $MF_{1},\ \ MF_{2}$ được gọi là bán kính qua tiêu điểm.

2) Phương trình chính tắc của elip

Với $F_{1}( - c;0),\ \ F_{2}(c;0)$ $F_{1}( - c;0),\ \ F_{2}(c;0)$:

$M(x;y) \in (E) \Leftrightarrow \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ \ \ (1)$ $M(x;y) \in (E) \Leftrightarrow \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ \ \ (1)$ trong đó $b^{2} = a^{2} - c^{2}$ $b^{2} = a^{2} - c^{2}$

(1) được gọi là phương trình chính tắc của $(E).$

3) Hình dạng và tính chất của elip

Elip có phương trình (1) nhận các trục tọa độ là trục đối xứng và gốc tọa độ làm tâm đối xứng.

+ Tiêu điểm: Tiêu điểm trái $F_{1}( - c;0),$ $F_{1}( - c;0),$ tiêu điểm phải $F_{2}(c; 0)$ $F_{2}(c; 0)$

+ Các đỉnh: $A_{1}( - a;0),\ \ A_{2}(a;0),\ \ B_{1}(0; - b),\ \ B_{2}(0;b)$ $A_{1}( - a;0),\ \ A_{2}(a;0),\ \ B_{1}(0; - b),\ \ B_{2}(0;b)$

+ Trục lớn: $A_{1}A_{2} =2a$ $A_{1}A_{2} =2a$, nằm trên trục $Ox;$ trục nhỏ: $B_{1}B_{2} =2b$ $B_{1}B_{2} =2b$, nằm trên trục $Oy.$

+ Hình chữ nhật tạo bởi các đường thẳng $x = \pm a,\ y = \pm b$ $x = \pm a,\ y = \pm b$ gọi là hình chữ nhật cơ sở.

+ Tâm sai: $e = \frac{c}{a} < 1$ $e = \frac{c}{a} < 1$

+ Bán kính qua tiêu điểm của điểm $M\left( x_{M};y_{M} \right)$ $M\left( x_{M};y_{M} \right)$ thuộc $(E)$ là:

$MF_{1} = a + ex_{M} = a + \frac{c}{a}x_{M},\ \ MF_{2} = a - ex_{M} = a - \frac{c}{a}x_{M}$ $MF_{1} = a + ex_{M} = a + \frac{c}{a}x_{M},\ \ MF_{2} = a - ex_{M} = a - \frac{c}{a}x_{M}$

II. Các dạng toán thường gặp và phương pháp giải chi tiết

Dạng 1: Xác định độ dài các trục khi cho sẵn phương trình elip.

Phương pháp giải

Từ phương trình chính tắc của $(E) \Leftrightarrow \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\$ $(E) \Leftrightarrow \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\$ta có thể xác định được:

+ Các đỉnh: $A_{1}( - a;0),\ \ A_{2}(a;0),\ \ B_{1}(0; - b),\ \ B_{2}(0;b)$ $A_{1}( - a;0),\ \ A_{2}(a;0),\ \ B_{1}(0; - b),\ \ B_{2}(0;b)$

+ Trục lớn: $A_{1}A_{2}= 2a,$ $A_{1}A_{2}= 2a,$ trục nhỏ : $B_{1}B_{2} = 2b.$ $B_{1}B_{2} = 2b.$

Dạng 2: Xác định tọa độ các tiêu điểm khi cho sẵn phương trình elip

Phương pháp giải

Từ phương trình chính tắc của $(E) \Leftrightarrow \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\$ $(E) \Leftrightarrow \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\$ta có thể xác định được:

+ Các đỉnh: $A_{1}( - a;0),\ \ A_{2}(a;0),\ \ B_{1}(0; - b),\ \ B_{2}(0;b)$ $A_{1}( - a;0),\ \ A_{2}(a;0),\ \ B_{1}(0; - b),\ \ B_{2}(0;b)$

+ Tiêu điểm: Tiêu điểm trái $F_{1}( - c;0),$ $F_{1}( - c;0),$ tiêu điểm phải $F_{2}(c; 0)$ $F_{2}(c; 0)$ với $b^{2} = a^{2} - c^{2}$ $b^{2} = a^{2} - c^{2}$

Dạng 3: Xác định tọa độ các tiêu điểm khi cho sẵn phương trình elip.

Phương pháp giải

Từ phương trình chính tắc của $(E) \Leftrightarrow \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\$ $(E) \Leftrightarrow \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\$ta có thể xác định được:

+ Các đỉnh: $A_{1}( - a;0),\ \ A_{2}(a;0),\ \ B_{1}(0; - b),\ \ B_{2}(0;b)$ $A_{1}( - a;0),\ \ A_{2}(a;0),\ \ B_{1}(0; - b),\ \ B_{2}(0;b)$

Dạng 4: Lập phương trình chính tắc của elip, biết độ dài trục lớn và trục nhỏ.

Phương pháp giải

+ Trục lớn: $A_{1}A_{2} =2a,$ $A_{1}A_{2} =2a,$ trục nhỏ : $B_{1}B_{2} = 2b.$ $B_{1}B_{2} = 2b.$ Ta xác định được $a,\ \ b.$ $a,\ \ b.$

+ Viết phương trình elip: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ .$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ .$

Dạng 5: Lập phương trình chính tắc elip, biết độ dài trục lớn và tiêu cự của nó.

Phương pháp giải

+ Trục lớn : $A_{1}A_{2} =2a,$ $A_{1}A_{2} =2a,$ tiêu cự: $F_{1}F_{2} =2c.$ $F_{1}F_{2} =2c.$ Ta xác định: $b^{2} = a^{2} - c^{2}$ $b^{2} = a^{2} - c^{2}$

+ Viết phương trình elip: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ .$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ .$

Dạng 6: Lập phương trình chính tắc của elip khi biết độ dài trục nhỏ và tiêu cự của nó.

Phương pháp giải

+ Trục nhỏ : $B_{1}B_{2} = 2b,$ $B_{1}B_{2} = 2b,$ tiêu cự: $F_{1}F_{2} =2c.$ $F_{1}F_{2} =2c.$ Ta xác định: $a^{2} = b^{2} + c^{2}.$ $a^{2} = b^{2} + c^{2}.$

+ Viết phương trình elip: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ .$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ .$

Dạng 7: Lập phương trình chính tắc của elip, biết nó đi qua hai điểm cho trước.

Phương pháp giải tự luận

+ Phương trình elip có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ .$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ .$

+ Elip qua hai điểm cho trước, ta thay tọa độ vào phương trình elip giải ra được $a^{2},\ \ b^{2}.$ $a^{2},\ \ b^{2}.$

Phương pháp giải trắc nghiệm, casio

Dùng máy tính nhập: $\frac{X^{2}}{25} + \frac{Y^{2}}{9} \Rightarrow$ $\frac{X^{2}}{25} + \frac{Y^{2}}{9} \Rightarrow$ calc $X = 0;Y = 3$ và calc $X = 3;Y = - \frac{12}{5}$ $X = 3;Y = - \frac{12}{5}$ .

Kết quả ra bằng $1$ là đáp án đúng.

Dạng 8: Lập phương trình chính tắc của elip khi biết nó có một tiêu cự và đi qua một điểm cho trước.

Phương pháp giải

+ Phương trình elip có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ .$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\ .$

+ Từ giả thiết ta xác định được $c$ và $c^{2} = a^{2} - b^{2}.\ (1)$ $c^{2} = a^{2} - b^{2}.\ (1)$

+ Elip qua hai điểm $\left( x_{o},y_{o} \right)$ $\left( x_{o},y_{o} \right)$ cho trước, ta được: $\frac{x_{o}^{2}}{a^{2}} + \frac{y_{o}^{2}}{b^{2}} = 1\ .\ (2)$ $\frac{x_{o}^{2}}{a^{2}} + \frac{y_{o}^{2}}{b^{2}} = 1\ .\ (2)$

+ Từ $(1);(2)$ ta giải ra được $a^{2},\ \ b^{2}.$ $a^{2},\ \ b^{2}.$

Dạng 9: Chứng minh một điểm $M$ luôn di động trên một elip với điều kiện cho trước.

Phương pháp giải

Để chứng tỏ điểm $M$ di động trên một elip ta có hai cách sau:

Cách 1: Chứng minh tổng khoảng cách từ $M$ đến hai điểm cố định $F_{1},\ \ F_{2}$ $F_{1},\ \ F_{2}$ là một hằng số $2a\ \ (F_{1}F_{2} < 2a).$ $2a\ \ (F_{1}F_{2} < 2a).$

Khi đó $M$ di động trên elip có hai tiêu điểm $F_{1}, F_{2}$ $F_{1}, F_{2}$ và trục lớn là $2a.$

Cách 2: Chứng minh trong mặt phẳng tọa độ $Oxy$ điểm $M(x;y)$ có tọa độ thỏa mãn phương trình: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ với $a,\ \ b$ $a,\ \ b$ là hai hằng số thỏa mãn $0 < b < a.$

Dạng 10: Tìm số giao điểm của đường thẳng và elip.

Phương pháp giải

+ Phương trình elip có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$và đường thẳng $\Delta:y = mx + n.$ $\Delta:y = mx + n.$

+ Ta xét phương trình: $\frac{x^{2}}{a^{2}} + \frac{(mx + n)^{2}}{b^{2}} = 1\ \ \ (*)$ $\frac{x^{2}}{a^{2}} + \frac{(mx + n)^{2}}{b^{2}} = 1\ \ \ (*)$. Ta có 3 trường hợp:

TH1: $(*)$ có 2 nghiệm thì số giao điểm là 2 (đường thẳng cắt elip).

TH2: $(*)$ có 1 nghiệm thì số giao điểm là 1 (đường thẳng tiếp xúc elip).

TH3: $(*)$ vô nghiệm thì số giao điểm là 0 (đường thẳng và elip không có điểm chung).

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.

----------------------------------------

Qua bài viết này, bạn đã nắm được cấu trúc phương trình elip, ý nghĩa các tham số và cách vận dụng để giải bài tập Toán lớp 10 một cách chính xác. Hãy luyện tập thêm các dạng bài để củng cố kiến thức và tăng tốc độ làm bài. Đừng quên theo dõi những bài viết tiếp theo để cập nhật thêm phương pháp học hiệu quả và các chuyên đề hình học giải tích quan trọng khác.

Tải về

Chọn file muốn tải về: