Giải các bài toán thực tế ứng dụng hàm số bậc hai: Phương pháp và hướng dẫn chi tiết
Dạng toán thực tế hàm số bậc hai lớp 10
Trong chương trình Toán 10, các bài toán thực tế gắn với hàm số bậc hai luôn là dạng bài quan trọng, vừa rèn kỹ năng tư duy mô hình hóa, vừa giúp học sinh hiểu rõ ứng dụng của toán học trong đời sống. Bài viết này sẽ cung cấp phương pháp giải chi tiết, quy trình nhận dạng dạng toán, cùng nhiều ví dụ minh họa thực tế như bài toán năng suất, hình học, chuyển động, tối ưu sản xuất,... Từ đó giúp bạn chủ động vận dụng hàm số bậc hai vào giải quyết các tình huống đời sống một cách logic và hiệu quả.
A. ĐỀ BÀI CÁC BÀI TOÁN THỰC TẾ
I. TRẮC NGHIỆM
Câu 1: Biết một viên đạn được bắn ra theo quỹ đạo là một parabol có phương trình 
\(s(t) = - (t - 3)^{2} + 9\ \ \
(km)\), với \(t\) là thời gian tính bằng giây. Hỏi khi nào viên đạn đạt độ cao \(8\ km\)?
A. \(t = 4\ s\). B. \(t = 5\ s\). C. \(t = 3s\). D. \(t = 2\ s\).
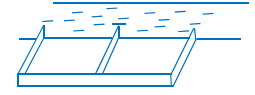
Câu 2: Một người nông dân có \(15.000.000\) vnđ để làm một cái hàng rào hình chữ \(E\) dọc theo một con sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là \(60.000\) vnđ/m, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là \(50.000\) vnđ/m. Tìm diện tích lớn nhất của đất rào thu được.
A. 50 \(m^{2}\). B. 3125 \(m^{2}\). C. 1250 \(m^{2}\). D. \(6250\) \(m^{2}\).
Câu 4: Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ \(Oth\),trong đó \(t\) là thời gian (tính bằng giây ), kể từ khi quả bóng được đá lên; \(h\) là độ cao( tính bằng mét ) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao \(1,2m\). Sau đó \(1\) giây, nó đạt độ cao \(8,5m\) và \(\left|
2x^{2} + x - 3 \right| = \left\{ \begin{matrix}
2x^{2} + x - 3 & khi & 2x^{2} + x - 3 \geq 0 \\
- \left( 2x^{2} + x - 3 \right) & khi & 2x^{2} + x - 3 < 0
\end{matrix} \right.\) giây sau khi đá lên, nó ở độ cao \(6m\). Hãy tìm hàm số bậc hai biểu thị độ cao \(h\) theo thời gian \(t\) và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.
A. \(y = 4,9t^{2} + 12,2t + 1,2\). B. \(y = - 4,9t^{2} + 12,2t +
1,2\).
C. \(y = - 4,9t^{2} + 12,2t - 1,2\). D. \(y = - 4,9t^{2} - 12,2t +
1,2\).
Câu 5: Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có \(n\) con cá thì trung bình mỗi con cá sau một vụ cân nặng \(P(n) = 360 -
10n\)(gam). Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lương cá sau một vụ thu được nhiều nhất?
A. \(12\). B. \(18\). C. \(36\). D. \(40\).
Câu 6: Một của hàng buôn giày nhập một đôi với giá là \(40\) đôla. Cửa hàng ước tính rằng nếu đôi giày được bán với giá \(x\) đôla thì mỗi tháng khách hàng sẽ mua \((120 -
x)\) đôi. Hỏi của hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?
A. \(80\) USD. B. \(160\) USD. C. \(40\) USD. D. \(240\) USD.
(Còn tiếp)
II. TỰ LUẬN
Bài tập 1: Biết một viên đạn được bắn ra, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Quỹ đạo của viên đạn trong mặt phẳng với hệ tọa độ \(Ots\) là một cung parabol có phương trình là \(s(t) = - (t - 2)^{2} + 16\)trong đó \(t\) là thời gian (tính bằng giây ), kể từ khi viên đạn được bắn ra; \(s\) là độ cao( tính bằng km ) của viên đạn.
a) Tính độ cao của viên đạn khi bắn được \(3s\)
b) Hỏi khi nào viên đạn đạt độ cao \(7\
km\)?
c) Khi nào viên đạn đạt độ cao lớn nhất.
d) Khi nào viên đạn chạm mặt đất.
Bài tập 2: Một quả bóng được ném vào không trung có chiều cao tính từ lúc bắt đầu ném ra được cho bởi công thức \(h(t) = - t^{2} + 2t + 3\) (tính bằng mét), t là thời gian tính bằng giây \((t
\geq 0)\).
a. Tính chiều cao lớn nhất quả bóng đạt được.
b. Hãy tính xem sau bao lâu quả bóng sẽ rơi xuống mặt đất ?
Bài tập 3: Một quả bóng được ném lên trên theo phương thẳng đứng từ mặt đất với vận tốc ban đầu \(14,7\
(m/s)\). Khi bỏ qua sức cản của không khí, độ cao của quả bóng so với mặt đất (tính bằng mét) được mô tả bởi công thức \(h(t) = - 4,9t^{2} + 14,7t\) .
a. Sau khi ném bao nhiêu giây thì quả bóng đạt độ cao lớn nhất?
b. Tìm độ cao lớn nhất của quả bóng?
c) Sau khi ném bao nhiêu giây thì quả bóng rơi chạm đất ?
Bài tập 4: Bác Hùng dùng \(200\
m\)hàng rào dây thép gai để rào miếng đất đủ rộng thành một mảnh vườn hình chữ nhật.
a) Gọi \(x\ (m)\)là chiều rộng của mảnh vườn đó, tìm công thức diện tích \(S(x)\) theo \(x.\)
b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất có thể rào được.
Bài tập 5: Bác An dùng \(60(m)\) lưới thép gai rào thành một mảnh vườn hình chữ nhật để trồng hoa.
a) Tính diện tích mảnh vườn hình chữ nhật rào được theo chiều rộng \(x\) (mét) của nó.
b) Tìm kích thước của mảnh vườn hình chữ nhật có diện tích lớn nhất mà bác An có thể rào được.
(Còn tiếp)
B. HƯỚNG DẪN GIẢI CHI TIẾT
I. TRẮC NGHIỆM
Câu 1.
Chọn D
Quả đạn đạt độ cao \(8\ km\) khi
\(s(t) = 8 \Leftrightarrow - (t - 3)^{2} +
9 = 8 \Leftrightarrow (t - 3)^{2} = 1 \Leftrightarrow \left\lbrack
\begin{matrix}
t = - 1\ \ (KTM) \\
t = 2\ \ \ \ \ (TM)
\end{matrix} \right.\) Parabol
Câu 2.
Phân tích ta đặt các kích thước của hàng rào như hình vẽ:
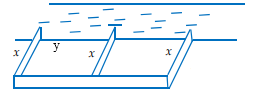
Giá thành làm rào là:
\(3x.50\ 000 + 2y.60\ 000 = 15\ 000\
000\) ⇔ \(5x + 4y = 5\ 00\) ⇔ \(y = \frac{500 - 5x}{4}\).
Diện tích khu vườn sau khi được rào là: \(S(x) = x.2y = x.2.\frac{500 - 5x}{4} = -
\frac{5}{2}x^{2} + 250x\).
Diện tích khu vườn lớn nhất khi hàm số \(S(x) = - \frac{5}{2}x^{2} + 250x\) đạt giá trị lớn nhất.
Khi đó: \(S_{\max} = - \frac{\Delta}{4a} =
6250\) \(m^{2}\).
Vậy diện tích lớn nhất của đất rào thu được là \(6250\) \(m^{2}\).
(Còn tiếp)
II. TỰ LUẬN
Bài tập 1
a) Khi \(t = 3(s)\) thì \(s(3) = - (3 - 2)^{2} + 8\ = 15\ \
(km)\)
b) Viên đạn đạt độ cao \(7\ km\) khi \(s(t) = 4 \Leftrightarrow - (t - 2)^{2} + 16\
\ = 7 \Leftrightarrow \left\lbrack \begin{matrix}
t = 5 \\
t = - 1(KTM)
\end{matrix} \right.\)
Vậy khi bắn được \(5s\)thì viên độ có độ cao\(7\ km\)
c)Giá trị lớn nhất của \(s(t) = - (t -
2)^{2} + 16\\)là \(16\) khi \(t = 2\)
Vậy khi bắn viên đạn được \(2s\) thì viên đạn đạt độ cao lớn nhất là \(16\)km.
d) Ta có \(- (t - 2)^{2} + 16\ \ = 0
\Leftrightarrow (t - 2)^{2} = 16 \Leftrightarrow \left\lbrack
\begin{matrix}
t = 6 \\
t = - 2(KTM)
\end{matrix} \right.\)
Vậy sau \(6s\) thì viên đạn sẽ rơi xuống mặt đất.
Bài tập 2
a. Ta có: \(h(t) = - t^{2} + 2t + 3
\Leftrightarrow h(t) = - (t - 1)^{2} + 4 \Rightarrow \max h(t) = h(1) =
4\).
Vậy quả bóng đạt chiều cao lớn nhất bằng 4 m tại thời điểm \(t = 1\) giây.
b. Ta có: \(- t^{2} + 2t + 3 = 0
\Leftrightarrow t = - 1\) (loại) hoặc \(t = 3\) (nhận).
Vậy sau 3 giây quả bóng sẽ rơi xuống mặt đất.
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
--------------------------------------------
Thông qua hệ thống phương pháp, ví dụ và bài tập thực tế đa dạng, bạn hoàn toàn có thể tự tin xử lý mọi dạng bài ứng dụng của hàm số bậc hai trong chương trình Toán 10. Khi hiểu rõ bản chất mô hình hóa, việc tìm giá trị lớn nhất – nhỏ nhất, lập phương trình, phân tích tình huống… trở nên nhẹ nhàng và chủ động hơn rất nhiều.
