Hàm bậc hai lớp 10: Công thức, các dạng toán và bài tập có đáp án
Chuyên đề Toán 10: Hàm số bậc hai
Hàm bậc hai là một trong những chuyên đề trọng tâm của Toán 10, đóng vai trò nền tảng cho nhiều dạng bài quan trọng ở các lớp tiếp theo. Việc nắm chắc công thức, hiểu bản chất đồ thị và thành thạo các dạng toán giúp học sinh dễ dàng chinh phục mọi dạng bài từ cơ bản đến nâng cao. Trong chuyên đề Hàm bậc hai lớp 10 – Công thức, các dạng toán và bài tập có đáp án, bạn sẽ được hệ thống hoá toàn bộ kiến thức trọng tâm, kèm theo ví dụ minh họa và bộ bài tập có lời giải chi tiết. Đây là tài liệu hỗ trợ học nhanh – nhớ lâu, phù hợp để ôn tập, luyện thi, hoặc củng cố ngay sau mỗi bài học.
A. Hàm số bậc hai
Hàm số bậc hai là hàm số cho bởi công thức:
\(y = ax^{2} + bx + c\)
Trong đó \(x\) là biến số, \(a,b,c\) là các hằng số và \(a \neq 0\).
Tập xác định của hàm số bậc hai là \(\mathbb{R}\).
Chú ý:
+ Khi \(a = 0\), \(b \neq 0\), hàm số trở thành hàm số bậc nhất \(y = bx + c\).
+ Khi \(a = b = 0\), hàm số trở thành hàm hằng \(y = c\) .
B. Đồ thị của hàm số bậc hai
1. Nhắc lại kiến thức \(y = ax^{2},a \neq
0\)
Đồ thị hàm số \(y = ax^{2},a \neq
0\) là một parabol có đỉnh là gốc tọa độ, có trục đối xứng là trục tung (là đường thẳng \(x =
0\)).
Parabol này quay bề lõm lên trên nếu \(a
> 0\), xuống dưới nếu \(a <
0\).
2. Đồ thị hàm số \(y = ax^{2} + bx + c,a
\neq 0\)
Đồ thị hàm số \(y = ax^{2} + bx + c,a \neq
0\) là một parabol có:
+ Đỉnh \(I\left( - \frac{b}{2a}; -
\frac{\Delta}{4a} \right)\).
+ Trục đối xứng là đường thẳng \(x = -
\frac{b}{2a}\).
+ Bề lõm hướng lên trên nếu \(a >
0\), hướng xuống dưới nếu \(a <
0\).
+ Giao điểm với trục tung là \(M(0;c)\).
+ Số giao điểm với trục hoành bằng số nghiệm của phương trình \(ax^{2} + bx + c = 0\).
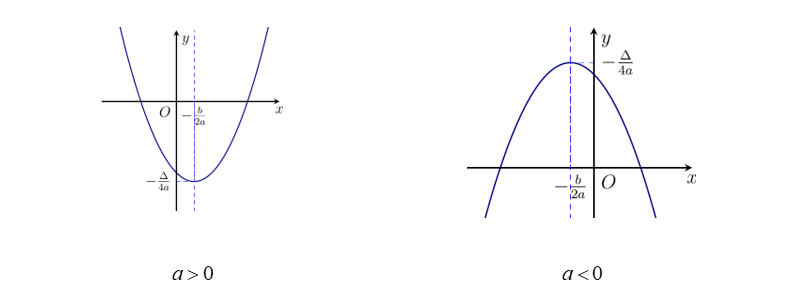
3. Cách vẽ đồ thị hàm số bậc hai
Vẽ đồ thị hàm số \(y = ax^{2} + bx +
c\) ta tiến hành các bước
- Bước 1. Xác định tọa độ đỉnh \(I\left( -
\frac{b}{2a}\ ;\ - \frac{\Delta}{4a} \right)\).
- Bước 2. Vẽ trục đối xứng \(x = -
\frac{b}{2a}.\)
- Bước 3. Xác định các giao điểm của parabol với các trục toạ độ(nếu có) và một vài điểm đặc biệt trên đồ thị.
- Bước 4. Vẽ parabol.( Khi vẽ parabol chú ý hệ số a để quay bề lõm lên trên hay xuống dưới)
4. Xét sự đơn điệu của hàm số bậc hai
Trường hợp 1. Với a > 0
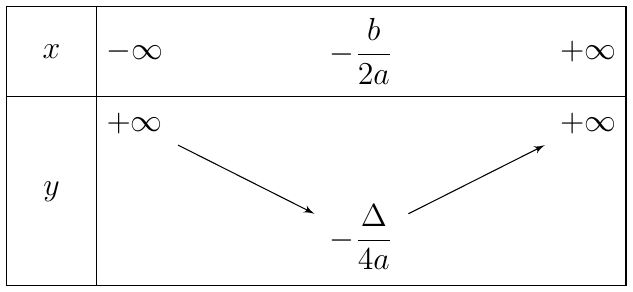
+ Hàm số đồng biến trên khoảng \(\left( -
\frac{b}{2a}; + \infty \right)\).
+ Hàm số nghịch biến trên khoảng \(\left( -
\infty; - \frac{b}{2a} \right)\).
+ Giá trị nhỏ nhất của hàm số là \(-
\frac{\Delta}{4a}\\)khi \(x = -
\frac{b}{2a}\).
Trường hợp 2. Với a < 0
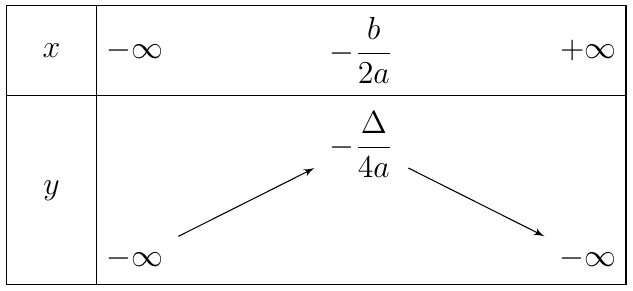
+ Hàm số đồng biến trên khoảng \(\left( -
\infty; - \frac{b}{2a} \right)\).
+ Hàm số nghịch biến trên khoảng \(\left( -
\frac{b}{2a}; + \infty \right)\).
+ Giá trị lớn nhất của hàm số là \(-
\frac{\Delta}{4a}\\)khi \(x = -
\frac{b}{2a}\)
C. Các dạng toán về hàm số bậc hai thường gặp
- Dạng 1. Nhận biết hàm số bậc hai. Xác định tọa độ đỉnh, trục đối xứng của (P)
- Dạng 2. Vẽ đồ thị hàm số bậc hai - Xác định chiều biến thiên của hàm số bậc hai
- Dạng 3. Sự tương giao của đồ thị hàm số bậc hai
- Dạng 4. Điểm cố định của đồ thị hàm số
- Dạng 5. Tìm hàm số bậc hai thỏa điều liện cho trước
- Dạng 6. Tìm GTLN, GTNN của hàm số bậc hai
- Dạng 7. Bài toán thức tế.
-------------------------------
Qua chuyên đề này, bạn đã được trang bị trọn bộ kiến thức từ định nghĩa, công thức, cách nhận dạng, đến phương pháp giải nhanh các dạng bài toán liên quan đến hàm bậc hai lớp 10. Những bài tập tự luyện có đáp án đi kèm sẽ giúp bạn củng cố kiến thức và tăng tốc độ xử lý bài thi. Hãy lưu lại bài viết để tiện xem lại khi cần và tiếp tục mở rộng kiến thức với các chuyên đề tiếp theo của Toán 10. Đừng quên chia sẻ bài viết nếu bạn thấy hữu ích – điều đó sẽ giúp nhiều học sinh khác học tốt hơn chủ đề Hàm số bậc hai. Chúc bạn học tập hiệu quả và đạt kết quả cao trong mọi kỳ kiểm tra!
