Bất phương trình chứa dấu giá trị tuyệt đối
Bài tập bất phương trình giá trị tuyệt đối Toán 10 có đáp án
Bất phương trình chứa dấu giá trị tuyệt đối là dạng toán quan trọng trong chương trình Toán 10, thường gây khó khăn cho học sinh do phải xét nhiều trường hợp và dễ sai điều kiện.
Bài viết này hệ thống cách giải bất phương trình giá trị tuyệt đối từ cơ bản đến nâng cao, kèm bài tập Toán 10 có đáp án, giúp học sinh nắm chắc phương pháp và làm bài chính xác hơn.
Bài tập 1. Tập nghiệm của phương trình ![]() có tất cả bao nhiêu số nguyên?
có tất cả bao nhiêu số nguyên?
A. Vô số. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Chọn C
Ta có:
![]()


![]() .
.
Với ![]() .
.
Bài tập 2. Tìm tập nghiệm của bất phương trình: ![]() .
.
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Chọn A
Do ![]() ,
, ![]() nên bất phương trình
nên bất phương trình ![]() vô nghiệm.
vô nghiệm.
Bài tập 3. Tìm ![]() để
để ![]() với mọi số thực
với mọi số thực ![]() ?
?
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Chọn B
Cách 1: Ta có:
![]()
![]() .
.
Do ![]()
nên bất phương trình đúng với mọi số thực ![]() .
.
Cách 2: Ta có ![]() với
với ![]() .
.
Vậy ![]() với mọi số thực
với mọi số thực ![]()
![]()
 .
.
Cách 3: Tự luận
Ta có:
![]()
![]() .
.
Xét hàm số ![]() .
.

TH1: ![]() .
.
BBT:
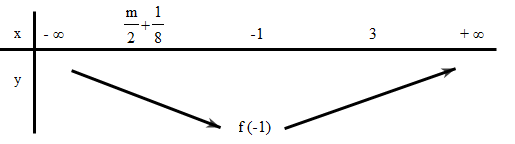
Để ![]()
![]()
![]()
![]() .
.
TH2: ![]()
![]() .
.
BBT:
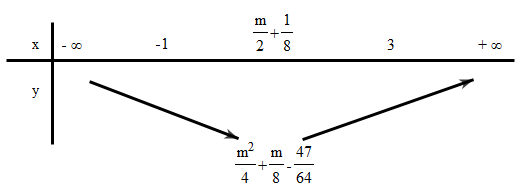
Để ![]()
![]()
 .
.
TH3: ![]()
![]() .
.
BBT:

Để ![]()
![]()
![]() .
.
![]() Kết hợp 3 trường hợp ta có
Kết hợp 3 trường hợp ta có ![]() .
.
📄 Do dung lượng nội dung lớn, tài liệu chi tiết được cung cấp dưới dạng file tải về.
-----------------------------------------------
Nắm vững cách giải bất phương trình chứa dấu giá trị tuyệt đối sẽ giúp học sinh tự tin xử lý các bài toán Toán 10 và làm nền tảng cho những dạng nâng cao ở các lớp trên









