Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Hệ bất phương trình bậc hai một ẩn và các bài toán liên quan

Bất phương trình bậc hai một ẩn Toán 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Bài tập Toán 10: Hệ bất phương trình bậc hai một ẩn

Trong Toán 10, dạng hệ bất phương trình bậc hai một ẩn yêu cầu học sinh không chỉ giải từng bất phương trình mà còn xác định đúng giao của các tập nghiệm. Đây là dạng toán dễ sai nếu nhầm lẫn khi biểu diễn nghiệm trên trục số.

Bài viết Hệ bất phương trình bậc hai một ẩn và các bài toán liên quan hướng dẫn phương pháp giải rõ ràng – logic, giúp học sinh làm chủ các bài bất phương trình bậc hai Toán 10 một cách hiệu quả.

Cách giải hệ bất phương trình bậc hai một ẩn lớp 10

Bài tập 1. Tập nghiệm của hệ bất phương trình $\left\{ \begin{matrix} 5x - 2 < 4x + 5 \\ x^{2} < (x + 2)^{2} \end{matrix} \right.$ có dạng . Khi đó tổng bằng?

A. B. C. D.

Hướng dẫn giải

Chọn B

Ta có: $\left\{ \begin{matrix} 5x - 2 < 4x + 5 \\ x^{2} < (x + 2)^{2} \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} 5x - 2 < 4x + 5 \\ x^{2} < x^{2} + 4x + 4 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x < 7 \\ x > - 1 \end{matrix} \right.$ .

Vậy tập nghiệm của phương trình là: . Suy ra

Bài tập 2. Tập nghiệm của hệ bất phương trình $\left\{ \begin{matrix} x - \frac{1}{2} \geq \frac{x}{4} + 1 \\ x^{2} - 4x + 3 \leq 0 \end{matrix} \right.$ là

A. . B. $( - \infty;2\rbrack \cup \lbrack 3; + \infty)$ . C. $S = \lbrack 2;3\rbrack$ . D. $( - \infty;2) \cup (3; + \infty)$ .

Hướng dẫn giải

Chọn C

Ta có:

$\left\{ \begin{matrix} x - \frac{1}{2} \geq \frac{x}{4} + 1 \\ x^{2} - 4x + 3 \leq 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} \frac{3}{4}x \geq \frac{3}{2} \\ 1 \leq x \leq 3 \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} x \geq 2 \\ 1 \leq x \leq 3 \end{matrix} \right.\ \Leftrightarrow 2 \leq x \leq 3.$

Vậy tập nghiệm của hệ bất phương trình là $S = \lbrack 2;\ 3\rbrack$ .

Bài tập 3. Tập nghiệm của hệ bất phương trình $\left\{ \begin{matrix} x^{2} - 6x + 5 \leq 0 \\ x^{2} - 8x + 12 < 0 \end{matrix} \right.$ là

A. $\lbrack 2;\ 5\rbrack$ . B. $\lbrack 1;\ 6\rbrack$ . C. $(2;\ 5\rbrack$ . D. $\lbrack 1;\ 2\rbrack \cup \lbrack 5;\ 6\rbrack$ .

Hướng dẫn giải

Chọn C

Ta có: $\left\{ \begin{matrix} x^{2} - 6x + 5 \leq 0 \\ x^{2} - 8x + 12 < 0 \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} 1 \leq x \leq 5 \\ 2 < x < 6 \end{matrix} \right.\ \Leftrightarrow 2 < x \leq 5$ .

Bài tập 4. Tìm tập xác định của hàm số $y= \sqrt{x^{2} - 2x} + \frac{1}{\sqrt{25 - x^2}}$ ?

A. $D = ( - 5;0\rbrack \cup \lbrack 2;5)$ . B. $D = ( - \infty;0\rbrack \cup \lbrack 2; + \infty)$ .

C. . D. $D = \lbrack - 5;0\rbrack \cup \lbrack 2;5\rbrack$ .

Hướng dẫn giải

Chọn A

Điều kiện: $\left\{ \begin{matrix} x^{2} - 2x \geq 0 \\ 25 - x^{2} > 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} \left\lbrack \begin{matrix} x \geq 2 \\ x \leq 0 \end{matrix} \right.\ \\ - 5 < x < 5 \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} - 5 < x \leq 0 \\ 2 \leq x < 5 \end{matrix} \right.$ .

Tập xác định: $D = ( - 5;0\rbrack \cup \lbrack 2;5)$ .

Bài tập 5. Hệ bất phương trình $\left\{ \begin{matrix} x^{2} - 4 < 0 \\ (x - 1)\left( x^{2} + 5x + 4 \right) \geq 0 \end{matrix} \right.$ có số nghiệm nguyên là

A. . B. . C. Vô số. D. .

Hướng dẫn giải

Chọn A

Ta có:

$\left\{ \begin{gathered} {x^2} - 4 < 0 \hfill \\ \left( {x - 1} \right)\left( {{x^2} + 5x + 4} \right) \geqslant 0 \hfill \\ \end{gathered} \right.$ $\Leftrightarrow \left\{ \begin{matrix} - 2 < x < 2 \\ \left\lbrack \begin{matrix} - 4 \leq x \leq - 1 \\ x \geq 1 \end{matrix} \right.\ \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} - 2 < x \leq - 1 \\ 1 \leq x < 2 \end{matrix} \right.$ 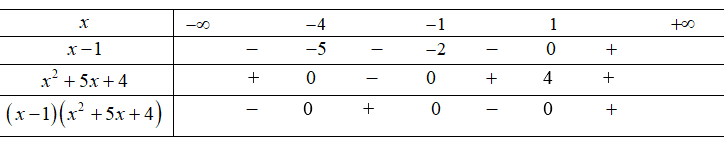do là số nguyên $\Leftrightarrow x = \left\{ - 1;1 \right\}$

Bài tập 6. Tập nghiệm của hệ bất phương trình $\left\{ \begin{matrix} x^{2} - 4x + 3 < 0 \\ - 6x + 12 > 0 \end{matrix} \right.$ là

A. . B. $(1;\ \ 4)$ . C. $( - \infty;\ \ 1) \cup (3; + \infty)$ . D. $( - \infty;\ \ 2) \cup (3; + \infty)$ .

Hướng dẫn giải

Chọn A

Ta có:

$\left\{ \begin{matrix} x^{2} - 4x + 3 < 0 \\ - 6x + 12 > 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} (x - 1)(x - 3) < 0 \\ - 6x > - 12 \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} 1 < x < 3 \\ x < 2 \end{matrix} \right.\ \Leftrightarrow 1 < x < 2$ .

Tập nghiệm của hệ bất phương trình là .

📥 Để xem trọn vẹn nội dung và ví dụ minh họa, bạn vui lòng tải tài liệu tham khảo tại đây.

------------------------------------------------------

Nắm vững cách giải hệ bất phương trình bậc hai một ẩn giúp học sinh xử lý nhanh và chính xác các bài toán Toán 10. Đây là kiến thức quan trọng để học tốt các nội dung về hàm số và bất phương trình ở các lớp trên.

Xem thử Tải về

Chọn file muốn tải về: