Phương trình Parabol trong mặt phẳng tọa độ
Chuyên đề Toán 10: Phương trình Parabol
Trong chương trình Toán 10, chủ đề Phương trình Parabol trong mặt phẳng tọa độ Oxy là kiến thức trọng tâm, xuất hiện thường xuyên trong bài tập, kiểm tra và đề thi. Việc nắm vững các dạng Parabol cơ bản, cách suy ra phương trình, dạng chuẩn, dạng tổng quát và ứng dụng vào bài toán thực tế giúp học sinh tăng tốc độ xử lý bài tập và nâng cao tư duy hình học – đại số.
A. TÓM TẮT LÝ THUYẾT
1. Định nghĩa Parabol
Cho điểm cố định F và đường thẳng cố định ∆ không đi qua F. Parabol (P) là tập hợp các điểm M cách đều điểm F và đường thẳng ∆.
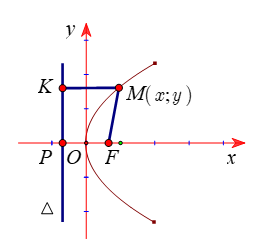
Điểm F gọi là tiêu điểm của parabol.
Đường thẳng ∆ được gọi là đường chuẩn của parabol
\(p = d(F;\Delta)\) được gọi là tham số của parabol.
2. Phương trình chính tắc của parabol
Với \(F\left( \frac{p}{2};0
\right)\) và \(\Delta:x = -
\frac{p}{2}(p > 0)\)
\(M(x;y) \in (P) \Leftrightarrow y^{2} =
2px\) (3)
Phương trình (3) được gọi là phương trình chính tắc của parabol
3. Hình dạng và tính chất của parabol
- Tiêu điểm \(F\left( \frac{p}{2};0
\right)\)
- Phương trình đường chuẩn: \(\Delta:x = -
\frac{p}{2}\)
- Gốc tọa độ O được gọi là đỉnh của parabol
- \(Ox\) được gọi là trục đối xứng
- \(M\left( x_{M};y_{M} \right)\) thuộc (P) thì: \(MF = d(M;\Delta) = x_{M} +
\frac{p}{2}\)
B. PHƯƠNG PHÁP HƯỚNG DẪN GIẢI TOÁN
Ví dụ 1: Viết phương trình của parabol biết:
a) Ox là trục đối xứng và tiêu điểm là \(F(4;0)\).
b) Ox là trục đối xứng và tiêu điểm là \(F(
- 2;0)\).
Hướng dẫn giải
a) Phương trình của parabol nhận Ox làm trục đối xứng là \(y^{2} = 2px\)
Vì \(F(4;0) \Rightarrow \frac{p}{2} = 4
\Rightarrow 2p = 16 \Rightarrow (P):y^{2} = 16x\)
b) Phương trình của parabol nhận Ox làm trục đối xứng là \(y^{2} = 2px\)
Vì \(F( - 2;0) \Rightarrow \frac{p}{2} = -
2 \Rightarrow 2p = - 8 \Rightarrow (P):y^{2} = - 8x\)
Ví dụ 2: Cho điểm \(M \in (P),y^{2} =
64x\) và \(N \in (D):4x + 3y + 46 =
0\).
a) Tìm tọa độ M, N để MN ngắn nhất.
b) Chứng minh với kết quả tìm được thì MN vuông góc với tiếp tuyến tại M của (P).
Hướng dẫn giải
a) Gọi \(M\left( \frac{m^{2}}{64};m \right)
\in (P)\)
\(d(m,(D)) = \frac{\left| \frac{4m^{2}}{64}
+ 3m + 46 \right|}{5} = \frac{1}{5}\left( \frac{m^{2}}{16} + 3m + 46
\right)\) (vì \(\frac{m^{2}}{16} + 3m +
46 > 0\)do \(\Delta <
0\))
Xét \(f(m) = \frac{m^{2}}{16} + 3m +
46\)
\(f'(m) = \frac{m}{8} + 3\), \(f'(m) = 0 \Leftrightarrow m = -
24\)
Vậy \(f(m)\) nhỏ nhất \(\Leftrightarrow d(M,(D)) \Leftrightarrow M(9; -
24)\)
b) Lúc đó phương trình tiếp tuyến của (P) tại M là:
\(yy_{M} = 32(x_{M} + x) \Leftrightarrow
y( - 24) = 32(x + 9) \Leftrightarrow 4x + 3y + 36 = 0\)
Phương trình đường thẳng qua M và vuông góc với (D) là: \(3x - 4y + m = 0\)
Điểm M thuộc tiếp tuyến \(\Rightarrow 3.9 - 4( - 24) + m = 0 \Rightarrow m =
- 123\)
Vậy phương trình đường thẳng qua M và vuông góc (D) là: \(3x - 4y - 123 = 0\)
\(N\left\{ \begin{matrix}
3x - 4y = 123 \\
4x + 3y = - 36
\end{matrix} \right.\)\(\Rightarrow \left\{ \begin{matrix}
x = \frac{37}{5} \\
y = - \frac{126}{5}
\end{matrix} \right.\ \Rightarrow N\left( \frac{37}{5};\frac{- 126}{5}
\right)\)
Do đó \(\overrightarrow{MN} = \left( -
\frac{8}{5}; - \frac{6}{5} \right)\) cùng phương với PVT của (D) là \(\overrightarrow{n} = (4;3)\)
Vậy MN vuông góc tiếp tuyến tại M.
Ví dụ 3: Trong mặt phẳng Oxy cho \(F(3;0)\)và đường thẳng \(d:3x - 4y + 16 = 0\)
a) Tìm khoảng cách từ F đến d, suy ra phương trình đường tròn tâm F và tiếp xúc với (d).
b) Viết phương trình parabol có tiêu điểm M và đỉnh là gốc tọa độ O. Chứng minh rằng parabol đó tiếp xúc với d. Tìm tọa độ điểm tiếp điểm.
Hướng dẫn giải
a) Ta có: \(d(F,d) = \frac{\left| 9 - 4(0)
+ 16 \right|}{\sqrt{9 + 16}} = 5\)
Vậy đường tròn tâm F, tiếp xúc với d có bán kính \(R = 5\).
Do đó phương trình là: \((x - 3)^{2} + (y -
0)^{2} = 25\)
b) Parabol tiêu điểm \(F(3;0)\), đỉnh \(\equiv O\)có phương trình là:
\(y^{2} = 2px\) với \(\frac{p}{2} = 3 \Rightarrow p = 6\)
Vậy (P) có phương trình \(y^{2} =
12x\)
Chứng minh (P) tiếp xúc với (d):
\((d):3x - 4y + 16 = 0 \Leftrightarrow x =
\frac{4y - 16}{3}\)
Phương trình tung độ giao điểm của d và (P) là:
\(y^{2} = 12\left( \frac{4y - 16}{3}
\right)\)\(\Leftrightarrow y^{2} - 16y + 64 = 0
\Leftrightarrow y_{1} = y_{2} = 8\)
Vì phương trình tung độ giao điểm có nghiệm kép nên d tiếp xúc với (P) tại tiếp điểm có \(y = 8 \Rightarrow x =
\frac{4.8 - 16}{3} = \frac{16}{3}\)
Vậy tiếp điểm là \(M\left( \frac{16}{3};8
\right)\).
C. BÀI TẬP TỰ RÈN LUYỆN CÓ HƯỚNG DẪN
Bài tập 1: Cho parabol \((P):y^{2} =
16x\)
a) Lập phương trình tiếp tuyến (P) sao cho vuông góc với đường thẳng \(3x - 2y + 6 = 0\).
b) Lập phương trình các tiếp tuyến với (P) đi qua điểm \(M( - 1;0)\).
Bài tập 2: Cho parabol \((P):y^{2} =
2x\)
a) Xác định đường chuẩn, tiêu điểm, vẽ (P).
b) Cho đường thẳng \((D):x - 2y + 6 =
0\). Tính khoảng cách ngắn nhất giữa (D) và (P).
Bài tập 3: Cho parabol \((P):y =
\frac{x^{2}}{2}\) và điểm \(A\left(
\frac{15}{8};\frac{27}{8} \right)\)
a) Viết phương trình đường thẳng qua \(M_{1}\left( - 1;\frac{1}{2} \right)\) và vuông góc với tiếp tuyến của (P) tại \(M_{1}\).
b) Tìm tất cả những điểm \(M \in
P\) sao cho AM vuông góc \(tt_{M}(P)\).
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
---------------------------------------
Hy vọng rằng thông qua những phân tích chi tiết và bài tập có đáp án trong chuyên đề Phương trình Parabol trong mặt phẳng tọa độ, bạn đã nắm rõ các bước lập phương trình, nhận diện dạng Parabol và vận dụng thành thạo vào bài toán Toán 10.
