Cách vẽ đồ thị hàm số bậc hai và xác định chiều biến thiên (Dễ hiểu – Có ví dụ)
Đồ thị hàm số bậc hai Toán 10
Đồ thị hàm số bậc hai (parabol) là nội dung trọng tâm trong chương trình Toán 10, giúp học sinh hiểu rõ sự biến thiên của hàm số và ứng dụng trong nhiều dạng bài thi. Tuy nhiên, nhiều bạn thường gặp khó khăn trong việc xác định dạng đồ thị, tìm đỉnh, hướng bề lõm và phân tích chiều biến thiên. Bài viết Cách vẽ đồ thị hàm số bậc hai và xác định chiều biến thiên (Dễ hiểu – Có ví dụ” sẽ hướng dẫn bạn quy trình từng bước để vẽ parabol chính xác, kèm ví dụ minh họa cụ thể. Đây là tài liệu chất lượng thuộc Chuyên đề Toán 10 Hàm số bậc hai, phù hợp cho học sinh muốn học nhanh – hiểu sâu – vận dụng tốt trong kiểm tra và thi cử.
A. Kiến thức cần nhớ
1. Cách vẽ đồ thị hàm số bậc hai
Thực hiện vẽ đồ thị hàm số 
\(y = ax^{2} + bx
+ c\) ta như sau:
-
Xác định tọa độ đỉnh
\(I\left( -
\frac{b}{2a}\ ;\ - \frac{\Delta}{4a} \right)\). -
Vẽ trục đối xứng
\(x = -
\frac{b}{2a}.\) -
Xác định các giao điểm của parabol với các trục toạ độ(nếu có) và một vài điểm đặc biệt trên đồ thị.
-
Vẽ parabol.( Khi vẽ parabol chú ý hệ số a để quay bề lõm lên trên hay xuống dưới)
2. Cách xét sự đồng biến nghịch biến của hàm số bậc hai
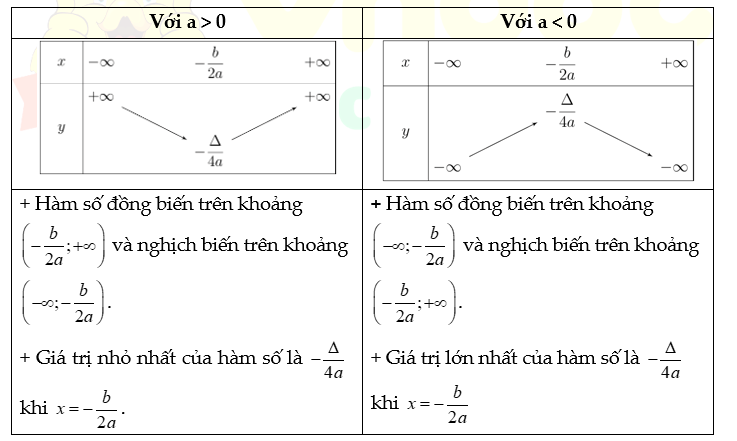
B. Bài tập ví dụ minh họa
Ví dụ 1: Cho đồ thị của hàm số bậc hai như hình vẽ:
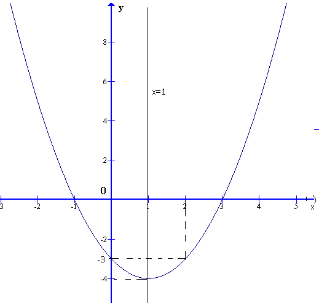
a) Tìm tọa độ đỉnh của đồ thị.
b) Tìm khoảng đồng biến, nghịch biến của hàm số.
c) Tìm giá trị nhỏ nhất của hàm số.
d) Tìm tập xác định và tập giá trị của hàm số.
Hướng dẫn giải
a)Tìm tọa độ đỉnh của đồ thị là \(I(1; -
4)\)
b) Hàm số đồng biến trên khoảng \((1; +
\infty)\) và nghịch biến trên khoảng \(( - \infty;1)\)
c) Giá trị nhỏ nhất cảu hàm số là \(y = -
4\) khi \(x = 1\)
d) Tập xác định của hàm số là \(R\), tập gái trị là \(\lbrack - 4; +
\infty)\)
Ví dụ 2: Tìm các khoảng đồng biến, nghịch biến và tìm giá trị nhỏ nhất của hàm số số \(f(x) = x^{2} - 4x +
5\)
?
Hướng dẫn giải
Xét hàm số\(f(x) = x^{2} - 4x + 5\) (\(a = 1 > 0\))
TXĐ: \(D\mathbb{= R}\).
Tọa độ đỉnh của đồ thị \(I(2;\
1)\).
Bảng biến thiên:
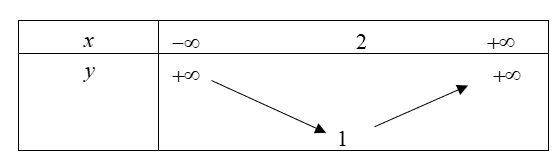
Vậy hàm số nghịch biến trên \(( - \infty;\
2)\), đồng biến trên \((2;\ +
\infty)\).
Giá trị nhỏ nhất của hàm số là \(y =
1\) khi \(x = 2.\)
Ví dụ 3. Cho hàm số \(y = f(x) = 3x^{2} -
2x - 1\) có đồ thị \((P)\).
a) Vẽ đồ thị \((P)\).
b) Từ đồ thị \((P)\) hãy tìm giá trị \(x\) sao cho \(y \leq 0.\)
c) Từ đồ thị \((P)\) hãy suy ra đồ thị của hàm số \(y = f(|x|)\)
d) Tìm \(m\) để phương trình \(\left| f(x) \right| - m = 0\) có 4 nghiệm phân biệt.
Hướng dẫn giải
a) Vẽ đồ thị \((P)\).
-
Tọa độ đỉnh
\(I\left( \frac{1}{3};\
\frac{- 4}{3} \right)\). -
Trục đối xứng là đường thẳng
\(x =
\frac{1}{3}.\) -
Giao điểm với trục tung
\(A(0; -
1)\) . -
Giao điểm với trục hoành
\(B(1;\ 0);\
C\left( - \frac{1}{3};\ 0 \right)\). -
Điểm đối xứng với
\(A(0; - 1)\) qua đường thẳng \(x = \frac{1}{3}\) là \(A\left( \frac{2}{3}; - 1
\right)\)
Đồ thị hình vẽ.
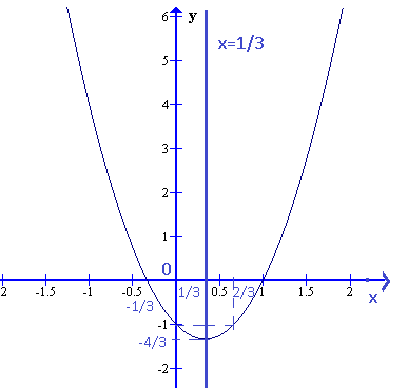
b) Từ đồ thị \((P)\) hãy tìm giá trị \(x\) sao cho \(y \leq 0\) là \(-
\frac{1}{3} \leq x \leq 1\).
c) Từ đồ thị \((P)\) hãy suy ra đồ thị của hàm số \(y = f(|x|)\)
Ta có \(y = f(|x|) = f(x)\) nếu \(x \geq 0\). Hơn nữa \(f(|x|) = f(| - x|)\) nên đồ thị hàm số \(y = f(|x|)\) nhận trục \(Oy\) làm trục đối xứng.
Do đó đồ thị hàm số \(y = f(|x|)\) gồm hai phần
Phần 1: là phần đồ thị \((P)\) phần nằm bên phải trục \(Oy\)
Phần 2: đối xứng của phần 1 qua trục \(Oy\).
Từ đó suy ra đồ thị hàm số \(y =
f(|x|)\) hình vẽ.
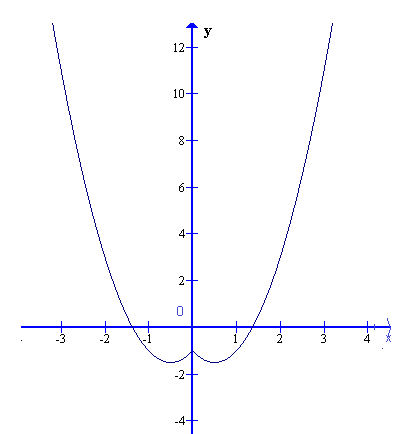
d) Tìm \(m\) để phương trình \(\left| f(x) \right| - m = 0\) có 4 nghiệm phân biệt.
Ta có \(\left| f(x) \right| - m = 0
\Leftrightarrow \left| f(x) \right| = m\)
Số nghiệm của phương trình \(\left| f(x)
\right| - m = 0\) là số giao điểm của đồ thị hàm số \(y = \left| f(x) \right|\)và đường thẳng \(y = m.\)
*Vẽ đồ thị hàm số \((P)\)
Ta có \(y = \left| f(x) \right| = \left\{
\begin{matrix}
f(x)\ \ \ \ khi\ \ f(x) \geq 0\ \ \\
- f(x)\ \ khi\ \ f(x) < 0
\end{matrix} \right.\).
Do đó đồ thị hàm số \(y = \left| f(x)
\right|\) gồm hai phần
Phần 1: là phần đồ thị \((P)\) phần nằm phía trên trục hoành
Phần 2: đối xứng với phần của \((P)\) nằm dưới trục hoành qua trục hoành.
Từ đó suy ra đồ thị hàm số \(y = \left|
f(x) \right|\) hình vẽ.
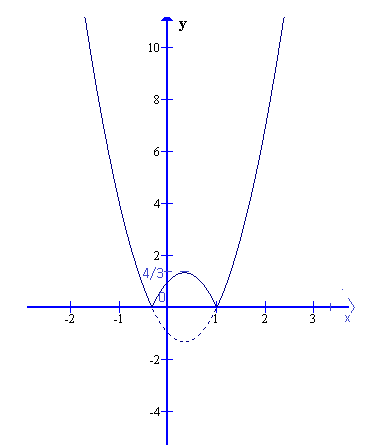
Để phương trình \(\left| f(x) \right| - m =
0\) có 4 nghiệm phân biệt thì đường thẳng \(y = m.\) cắt đồ thị hàm số \(y = \left| f(x) \right|\) tại 4 điểm phân biệt.
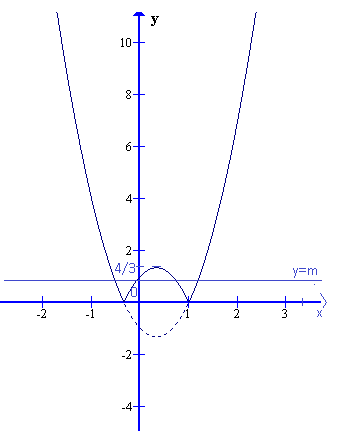
Dựa vào đồ thị ta suy ra \(0 < m <
\frac{4}{3}\) là giá trị cần tìm.
C. Bài tập vận dụng hàm số bậc hai có hướng dẫn chi tiết
Bài tập 1: Cho đồ thị của hàm số bậc hai như hình vẽ:
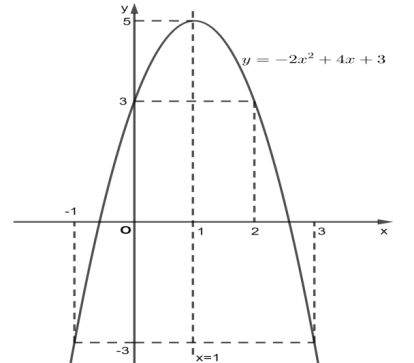
a) Tìm tọa độ đỉnh của đồ thị.
b) Tìm khoảng đồng biến, nghịch biến của hàm số.
c) Tìm giá trị lớn nhất của hàm số.
d) Tìm tập xác định và tập giá trị của hàm số.
Bài tập 2: Cho hàm số \(y = - x^{2} + 4x +
5\). Tìm các khoảng đồng biến, nghịch biến của hàm số. Tìm giá trị lớn nhất của hàm số.
Bài tập 3: Cho hàm số \(y = - 2x^{2} + 4x +
3\) có đồ thị là parabol \((P)\). Lập bảng biến thiên của hàm số đã cho và vẽ parabol \((P)\).
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
-------------------------------
Qua bài viết này, bạn đã được trang bị phương pháp vẽ đồ thị hàm số bậc hai một cách có hệ thống, đồng thời biết cách xác định chiều biến thiên dựa trên hệ số và đặc điểm của parabol. Các ví dụ minh họa giúp bạn củng cố kiến thức và tự tin áp dụng vào mọi dạng bài liên quan. Hãy lưu lại bài viết để ôn tập khi cần và tiếp tục khám phá các chủ đề khác trong Chuyên đề Toán 10. Chúc bạn học tốt và nâng cao kỹ năng phân tích đồ thị trong cả học tập lẫn các kỳ thi quan trọng!
