Phương trình đường chuẩn của Parabol (P)
Bài tập Toán 10: Phương trình đường chuẩn Parabol
Đường chuẩn của parabol là một yếu tố quan trọng giúp mô tả đầy đủ cấu trúc học của sơ đồ hàm số bậc hai trong chương trình Toán học 10. Làm rõ phương pháp đường chuẩn không chỉ hỗ trợ học sinh phân tích dạng sơ đồ mà còn giúp giải quyết các bài toán liên quan đến tiêu điểm, sức mạnh đối thoại và tính chất hình học của parabol. Bài viết này sẽ hướng dẫn bạn cách xác định phương pháp chuẩn hóa đường dẫn của parabol (P) một cách chi tiết, kèm theo bài tập minh họa có đáp án để bạn luyện tập hiệu quả.
A. Định nghĩa đường chuẩn
Cho điểm cố định F và đường thẳng cố định ∆ không đi qua F. Parabol (P) là tập hợp các điểm M cách đều điểm F và đường thẳng ∆.
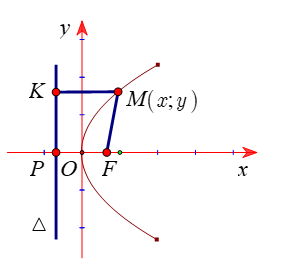
- Điểm F gọi là tiêu điểm của parabol.
- Đường thẳng ∆ được gọi là đường chuẩn của parabol.
Với 
\(F\left( \frac{p}{2};0
\right)\) và \(\Delta:x = -
\frac{p}{2}(p > 0)\)
\(M(x;y) \in (P) \Leftrightarrow y^{2} =
2px\) (3)
Khi đó (3) được gọi là phương trình chính tắc của parabol
- \(F\left( \frac{p}{2};0 \right)\) được gọi là tiêu điểm
- \(\Delta:x = - \frac{p}{2}\) được gọi là phương trình đường chuẩn
B. Ví dụ minh họa phương trình đường chuẩn của Parabol
Ví dụ 1. Viết phương trình của parabol biết tiêu điểm là \(F(0;1)\)và đường chuẩn \(y = - 1\)?
Hướng dẫn giải
Vì \(F(0;1) \in Oy\) \(\Rightarrow\) Phương trình \((P):x^{2} = 2py \Rightarrow \frac{p}{2} = 1
\Rightarrow 2p = 4\)
\(\Rightarrow (P):x^{2} = 4y\)
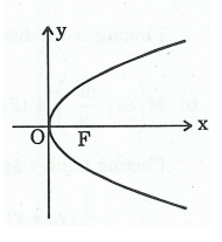
Ví dụ 2. Cho parabol \((P):y^{2} =
2x\). Xác định đường chuẩn, tiêu điểm, vẽ (P).
Hướng dẫn giải
Ta có \(y^{2} = 2x\) có dạng:
\(y^{2} = 2px \Rightarrow 2p = 2
\Rightarrow \frac{p}{2} = \frac{1}{2} \Rightarrow F\left( \frac{1}{2};0
\right)\)
\(\Rightarrow\) Phương trình đường chuẩn là \(x = - \frac{1}{2}\).
Hình vẽ minh họa bài toán:
Ví dụ 3. Cho Parabol \((P):y^{2} =
2px\) và đường thẳng \(D:2mx - y - mp =
0\). Gọi \(M',M''\)là giao điểm của (D) và (P). Chứng minh đường tròn đường kính \(M'M''\)tiếp xúc với đường chuẩn của (P).
Hướng dẫn giải
Hình vẽ minh họa bài toán:
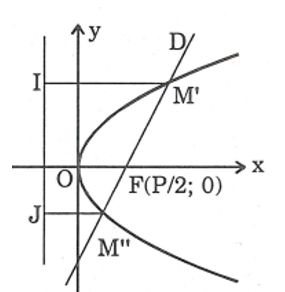
Ta có \((P):y^{2} = 2px\) có tiêu điểm \(\left( \frac{p}{2};0 \right) \in
(D)\)
Vẽ \(M'I,M''J\)lần lượt vuông góc với đường chuẩn \(\Delta\). Gọi (k) là trung điểm của \(M'M''\).
Vẽ \(KH\bot(\Delta)\).
Theo định nghĩa của parabol:
\(M'F = d(M',\Delta) =
M'I\)
\(M''F = d(M'',\Delta) =
M''J\)
Do đó KH là đường trung bình của hình thang \(IM'M''J\)nên ta có:
\(KH = d(K,\Delta) = \frac{M'I +
M''J}{2} = \frac{M'F + M''F}{2} =
\frac{M'M''}{2} = R\)
Vậy đường tròn đường kính \(M'M''\)tiếp xúc với đường chuẩn \(\Delta\).
C. Bài tập tự rèn luyện phương trình đường chuẩn có đáp án
Bài tập 1: Cho parabol \((P):y^{2} =
4x\). Chứng minh rằng từ một điểm N tùy ý trên đường chuẩn \(\Delta\)của (P) ta có thể kẻ được hai tiếp tuyến đến (P) và hai tiếp tuyến này vuông góc với nhau.
Bài tập 2. Cho parabol \((P)\) có phương trình chính tắc là \(y^{2} = -
2px\) với \(p > 0\). Phương trình đường chuẩn của \((P)\) là
A. \(y = - \frac{p}{2}\). B. \(y = \frac{p}{2}\). C. \(y = p\). D. \(y =
- p\).
Bài tập 3. Đường thẳng nào là đường chuẩn của parabol \(y^{2} = \frac{3}{2}x\)
A. \(x = - \frac{3}{4}.\) B. \(x = \frac{3}{4}.\) C.\(x = \frac{3}{2}.\) D. \(x = - \frac{3}{8}.\)
Bài tập 4. Đường thẳng nào là đường chuẩn của parabol \(y^{2} = - 4x\)?
A.\(x = 4.\) B.\(x = 2.\) C.\(x = 1.\) D. \(x = \pm 1.\)
Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!
----------------------------------------
Hy vọng bài viết đã giúp bạn nắm vững cách xác định phương pháp chuẩn hóa đường parabol và biết cách vận dụng vào các dạng bài Hàm số bậc hai Toán 10. Để hoàn thành toàn bộ đề tài này, hãy xem thêm các bài giải giải tập tự và mở rộng kiến thức với nhiều dạng sơ đồ khác nhau. Đừng quên theo dõi các bài học tiếp theo để nâng cao kỹ năng giải toán và cải thiện kết quả học tập của bạn.
