Giải phương trình bằng phương pháp biến đổi tương đương

Chuyên đề Toán học lớp 10: Giải phương trình bằng phương pháp biến đổi tương đương được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây nhé.

I/ Lý thuyết & Phương pháp giải

- Phương trình tương đương: Hai phương trình f₁(x) = g₁(x) và f₂(x) = g₂(x) được gọi là tương đương nếu chúng có cùng tập nghiệm

- Kí hiệu là f₁(x) = g₁(x) ⇔ f₂(x) = g₂(x)

- Phép biến đổi không làm thay đổi tập nghiệm của phương trình gọi là phép biến đổi tương đương.

- Phương trình hệ quả: f₂(x) = g₂(x) gọi là phương trình hệ quả của phương trình f₁(x) = g₁(x) nếu tập nghiệm của nó chứa tập nghiệm của phương trình f₁(x) = g₁(x)

- Kí hiệu là f₁(x) = g₁(x) ⇒ f₂(x) = g₂(x)

- Để giải phương trình ta thực hiện các phép biến đổi để đưa về phương trình tương đương với phương trình đã cho đơn giản hơn trong việc giải nó. Một số phép biến đổi thường sử dụng:

+ Cộng (trừ) cả hai vế của phương trình mà không làm thay đổi điều kiện xác định của phương trình ta thu được phương trình tương đương phương trình đã cho.

+ Nhân (chia) vào hai vế với một biểu thức khác không và không làm thay đổi điều kiện xác định của phương trình ta thu được phương trình tương đương với phương trình đã cho.

+ Bình phương hai vế của phương trình ta thu được phương trình hệ quả của phương trình đã cho.

Bình phương hai vế của phương trình (hai vế luôn cùng dấu) ta thu được phương trình tương đương với phương trình đã cho.

II. Ví dụ minh họa

Bài 1: Giải phương trình

Hướng dẫn:

Điều kiện:

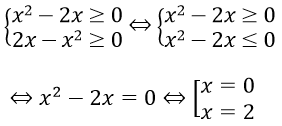
Thử lại ta thấy cả x = 0 và x = 2 đều thỏa mãn phương trình

Vậy tập nghiệm của phương trình là S = {0;2}

Bài 2: Giải phương trình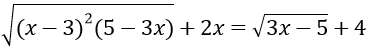

Hướng dẫn:

Điều kiện: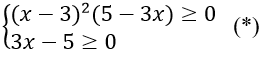

Ta thấy x = 3 thỏa mãn điều kiện (*)

Nếu x ≠ 3. thì (*)

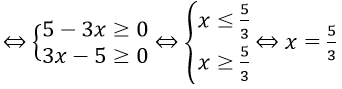
Do đó điều kiện xác định của phương trình là x = 3 hoặc x = 5/3

Thay x = 3 và x = 5/3 vào phương trình thấy chỉ có x = 3 thỏa mãn

Vậy phương trình đã cho có nghiệm duy nhất S = {3}

Bài 3: Giải phương trình

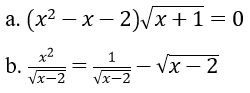
Hướng dẫn:

a. Điều kiện: x ≥ -1.

Ta có x = -1 là một nghiệm.

Nếu x > -1 thì √(x+1) > 0. Do đó phương trình tương đương

x² - x - 2 = 0 ⇔ x = -1 hoặc x = 2.

Đối chiếu điều kiện ta được nghiệm của phương trình là x = -1, x = 2.

Vậy phương trình đã cho có hai nghiệm S = {-1; 2}

b. ĐKXĐ: x > 2

Với điều kiện để phương trình tương đương với phương trình

x² = 1 - (x - 2)⇔ x² + x - 3 = 0

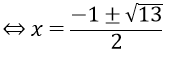
Đối chiếu với điều kiện ta thấy không có giá trị nào thỏa mãn

Vậy phương trình vô nghiệm

Bài 4: Giải phương trình

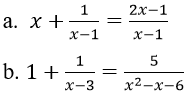
Hướng dẫn:

a. Điều kiện: x ≠ 1.

Với điều kiện trên phương trình tương đương x² - x + 1 = 2x - 1 ⇔ x = 1 hoặc x = 2

Đối chiếu điều kiện ta được phương trình có nghiệm duy nhất x = 2.

b. ĐKXĐ :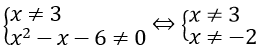

Với điều kiện trên phương trình tương đương với

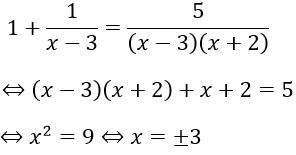
Đối chiếu với điều kiện ta có nghiệm của phương trình là x = -3

Bài 5: Tìm m để cặp phương trình sau tương đương

x² + mx - 1 = 0 (1) và (m-1)x² + 2(m-2)x + m - 3 = 0 (2)

Hướng dẫn:

Giả sử hai phương trình (1) và (2) tương đương

Ta có (m-1)x² + 2(m-2)x + m - 3 = 0

⇔

Do hai phương trình tương đương nên x = -1 cũng là nghiệm của phương trình (1)

Thay x = -1 vào phương trình (1) ta được m = 0

Với m = 0 thay vào hai phương trình ta thấy không tương đương.

Vậy không có giá trị nào của m thỏa mãn.

Với nội dung bài Giải phương trình bằng phương pháp biến đổi tương đương trên đây chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững phương pháp giải, công thức giải phương trình....

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Giải phương trình bằng phương pháp biến đổi tương đương. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài viết rồi đúng không ạ? Bài viết đã hướng dẫn bạn đọc giải phương trình bằng phương pháp biến đổi tương đương. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 10. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc