Cách xác định tập hợp

Chuyên đề Toán học lớp 10: Cách xác định tập hợp được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo.

Bài: Cách xác định tập hợp

Phương pháp giải

1: Với tập hợp A, ta có 2 cách:

Cách 1: liệt kê các phần tử của A: A={a₁; a₂; a₃;..}

Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của A

2: Tập hợp con

Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B, kí hiệu là A ⊂ B.

A ⊂ B ⇔ ∀x : x ∈ A ⇒ x ∈ B.

A ⊄ B ⇔ ∀x : x ∈ A ⇒ x ∉ B.

Tính chất:

1) A ⊂ A với mọi tập A.

2) Nếu A ⊂ B và B ⊂ C thì A ⊂ C.

3) ∅ ⊂ A với mọi tập hợp A.

Ví dụ minh họa

Ví dụ 1: Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó:

a) A={x ∈ R|(2x - x² )(2x² - 3x - 2)=0}.

b) B={n ∈ N|3 < n² < 30}.

Hướng dẫn:

a) Ta có:

(2x - x² )(2x² - 3x - 2) =0 ⇔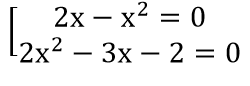

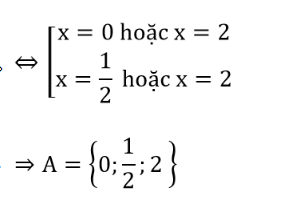
b) 3 < n² < 30 ⇒ √3 < |n| < √30

Do n ∈ N nên n ∈ {2;3;4;5}

⇒ B = {2;3;4;5}.

Ví dụ 2: Viết mỗi tập hợp sau bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó:

a) A = {2; 3; 5; 7}

b) B = {-3; -2; -1; 0; 1; 2; 3}

c) C = {-5; 0; 5; 10; 15}.

Hướng dẫn:

a) A là tập hợp các số nguyên tố nhỏ hơn 10.

b) B là tập hơp các số nguyên có giá trị tuyệt đối không vượt quá 3.

B={x ∈ Z||x| ≤ 3}.

c) C là tập hợp các số nguyên n chia hết cho 5, không nhỏ hơn -5 và không lớn hơn 15.

C={n ∈ Z|-5 ≤ n ≤ 15; n ⋮ 5}.

Ví dụ 3: Cho tập hợp A có 3 phần tử. Hãy chỉ ra số tập con của tập hợp A.

Hướng dẫn:

Giả sử tập hợp A={a;b;c}. Các tập hợp con của A là:

∅ ,{a},{b},{c},{a;b},{b;c},{c;a},{a;b;c}

Tập A có 8 phần tử

Chú ý: Tổng quát, nếu tập A có n phần tử thì số tập con của tập A là 2² phần tử.

Ví dụ 4: Cho hai tập hợp M={8k + 5 |k ∈ Z}, N={ 4l + 1 | l ∈ Z}. Khẳng định nào sau đây là đúng?

Hướng dẫn:

Rõ ràng ta có: M ≠ ∅ ; N ≠ ∅

Giả sử x là một phần tử bất kì của tập M, ta có x = 8k + 5 (k ∈ Z)

Khi đó, ta có thể viết x = 8k + 5 = 4(2k + 1) + 1 = 4l + 1 với l = 2k + 1 ∈ Z do k ∈ Z. Suy ra x ∈ N.

Vậy ∀x ∈ M ⇒ x ∈ N hay M ⊂ N.

Mặt khác 1 ∈ N nhưng 1 ∉ M nên N ⊄ M. Từ đó, suy ra M ≠ N

Vậy M ⊂ N.

Với nội dung bài Cách xác định tập hợp trên đây chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững phương pháp giải, cách xác định một tập hợp trong phép toán...

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Cách xác định tập hợp. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải SBT Toán 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc