Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Bài toán thực tế về ba đường Conic có đáp án

Toán thực tế lớp 10

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Ứng dụng elip parabol hyperbol trong thực tế

A. PHẦN ĐỀ BÀI
B. PHẦN ĐÁP ÁN

Trong chương trình Toán thực tế lớp 10, các bài toán liên quan đến ba đường Conic (Elip – Parabol – Hyperbol) luôn được xem là trọng tâm vì tính ứng dụng cao và khả năng rèn luyện tư duy hình học – đại số cho học sinh. Bài viết này tổng hợp những bài toán thực tế tiêu biểu nhất về ba đường Conic, kèm lời giải chi tiết, phân tích từng bước và đáp án chính xác, giúp bạn hiểu sâu bản chất, dễ dàng áp dụng vào các dạng bài thi và kiểm tra chương trình lớp 10.

A. PHẦN ĐỀ BÀI

Bài tập 1: Cổng chào của một thành phố dạng hình parabol có chiều cao h = 25m và khoảng cách giữa hai chân cổng là d = 120m. Hãy viết phương trình parabol của cổng chào.

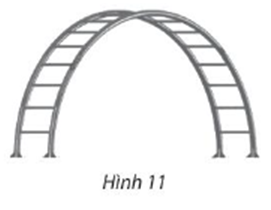
Bài tập 2: Thang leo gợi sóng cho trẻ em trong công viên có hai khung thép cong hình nửa elip cao 100cm và khoảng cách giữa hai chân là 240cm.

a) Hãy chọn hệ trục tọa độ tích hợp và viết phương trình chính tắc của elip trên.

b) Tính khoảng cách thẳng đứng từ một điểm cách chân khung 20cm lên đến khung thép.

Bài tập 3: Một tháp làm nguội của một nhà máy có mặt cắt là hình hypebol có phương trình

$\frac{x^{2}}{30^{2}} - \frac{y^{2}}{50^{2}} = 1\ .$ Biết chiều cao của tháp là 120m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng 0,5 khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp.

Bài tập 4: Gương phản chiếu của một đèn pha có mặt cắt là một parabol (P) với tim bóng đèn đặt ở tiêu điểm F. Chiều rộng giữa hai mép gương là $50\ cm$ , chiều sâu của gương là 40cm. Viết phương trình chính tắc của (P).

Bài tập 5: Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều rộng của hàm là 12m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8m thì có chiều rộng không quá 3m. Hỏi chiếc xe có chiều cao 2,8m có thể đi qua hầm được không?

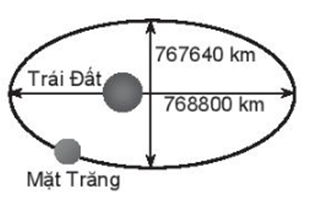
Bài tập 6: Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một đường elip với tâm Trái Đất là một tiêu điểm. Độ dài trục lớn, trục nhỏ của quỹ đạo lần lượt là 768 800km và 767 640 km. Tìm khoảng cách lớn nhất và bé nhất từ tâm của Trái Đất đến Mặt Trăng.

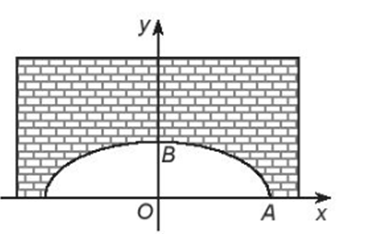
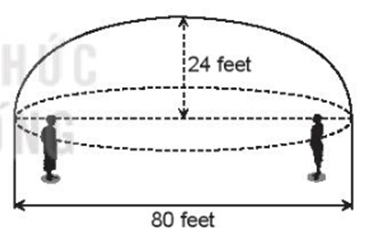
Bài tập 7: Hình vẽ bên minh họa một phòng thì thầm (whispering gallery) với mặt cắt ngang là một hình bán elip với chiều cao 24 feet và chiều rộng 80 feet. Một âm thanh được phát ra từ một tiêu điểm của phòng thì thầm có thể được nghe thấy tại tiêu điểm còn lại. hỏi hai người nói thì thầm qua lại với nhau thì sẽ cách trung tâm của phòng bao nhiêu mét? Theo đơn vị đo lường quốc tế 1 feet = 0,3048m.

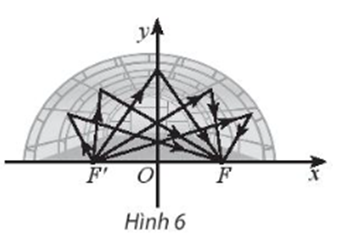
Bài tập 8: Một mái vòm nhà hát có mặt cắt là hình nửa elip. Cho biết khoảng cách giữa hai tiêu điểm là F'F = 50m và chiều dài của đường đi của một tia sáng từ F’ đến mái vòm rồi phản chiếu về F là 100m. Viết phương trình chính tắc của elip đó.

Bài tập 9: Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng một thời điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thuỷ thu và đo độ lệch thời gian. Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s. Từ thông tin trên, ta có thể xác định được tàu thuỷ thuộc đường hypebol nào? Viết phương trình chính tắc của hypebol đó theo đơn vị kilômét.

Bài tập 10: Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A điểm cuối là B, khoảng cách AB = 400m. Đỉnh parabol của khúc cua cách đường thẳng một khoảng 20 m và cách đều A, B.

a) Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng 1 m trên thực tế.

b) Lập phương trình chính tắc cùa (P), với 1 đơn vị đo trong mặt phẳng toạ độ tương ứng 1 km trên thực tế.

Bài tập 11: Một tháp triển lãm có mặt cắt hình hypebol có phương trình $\frac{x^{2}}{18^{2}} - \frac{y^{2}}{36^{2}} = 1\ .$

Cho biết chiều cao của tháp là 100m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp.

(Còn tiếp)

B. PHẦN ĐÁP ÁN

Bài tập 1

Chọn hệ trục tọa độ như hình vẽ:

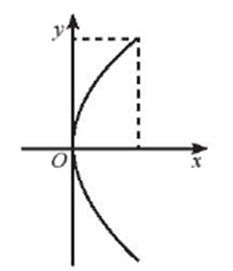
Phương trình của parabol có dạng $y^{2} = 2px$ .

Lúc đó parabol đi qua điểm M(25; 60). Thay tọa độ điểm M vào phương trình parabol ta được $60^{2} = 2p.25 \Rightarrow p = \frac{60^{2}}{50} = 72.$

Vậy phương trình của parabol là y²= 144x.

Bài tập 2

Chọn hệ trục tọa độ như hình vẽ:

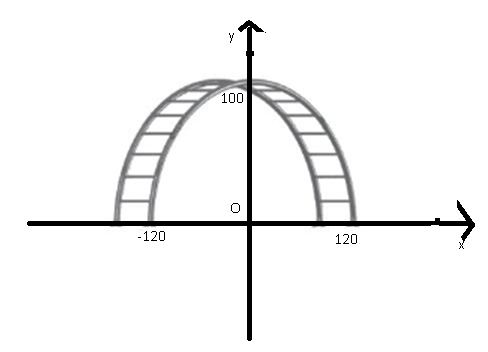
Khi đó ta có: 2a = 240 => a = 120; b = 100

Phương trình chính tắc của elip là $\frac{x^{2}}{120^{2}} + \frac{y^{2}}{100^{2}} = 1\ .$

Thay x = 120 - 20 = 100 vào phương trình của elip ta được là $\frac{100^{2}}{120^{2}} + \frac{y^{2}}{100^{2}} = 1\ \Rightarrow y = 100\sqrt{1 - \frac{100^{2}}{120^{2}}} \simeq 55\ \ \ (cm)$

Vậy khoảng cách thẳng đứng từ một điểm cách chân khung 20cm lên đến khung thép gần bằng 55 (cm).

Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!

----------------------------------------

Gợi ý tài liệu tham khảo:

Qua những bài toán thực tế về Elip, Parabol và Hyperbol cùng hướng dẫn chi tiết trong bài viết, hy vọng bạn đã hiểu rõ hơn cách vận dụng các tính chất của ba đường Conic vào đời sống cũng như trong bài tập Toán lớp 10. Hãy luyện tập thêm nhiều dạng bài để tư duy hình học – đại số của bạn ngày càng sắc bén hơn.

Tải về

Chọn file muốn tải về: