Ba đường Conic: Elip, Hypebol, Parabol
Tính chất và phương trình Elip, Hypebol, Parabol
Trong chương trình Toán lớp 10, chuyên đề Ba đường Conic: Elip, Hypebol, Parabol là một trong những nội dung quan trọng của hình học giải tích. Bài viết dưới đây sẽ giúp bạn hiểu rõ lý thuyết, tính chất, dạng phương trình và ứng dụng của từng đường Conic. Bên cạnh đó, các ví dụ minh họa và bài tập vận dụng sẽ hỗ trợ học sinh nắm chắc kiến thức và tự tin khi làm các dạng bài liên quan trong kiểm tra và thi học kì.
1. ELIP
- Cho hai điểm cố định và phân biệt 
\(F_{1}\), \(F_{2}\). Đặt \(F_{1}F_{2} = 2c > 0\). Cho số thực \(a\) lớn hơn \(c\). Tập hợp các điểm \(M\) sao cho \(MF_{1} + MF_{2} = 2a\) được gọi là đường elip. Hai điểm \(F_{1}\), \(F_{2}\) được gọi là hai tiêu điểm và \(F_{1}F_{2} = 2c\) được gọi là tiêu cự của elip đó.
Phương trình Elip
- Trong mặt phẳng tọa độ \(Oxy\), elip có hai tiêu điểm thuộc trục hoành sao cho \(O\) là trung điểm của đọan thẳng nối hai tiêu điểm đó thì có phương trình \(\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} =
1\), với \(a > b > 0\). \((2)\)
Ngược lại, mỗi phương trình có dạng \((2)\) đều là phương trình của elip có hai tiêu điểm \(F_{1}\left( - \sqrt{a^{2} -
b^{2}};0 \right)\), \(F_{2}\left(
\sqrt{a^{2} - b^{2}};0 \right)\) , tiêu cự \(2c = 2\sqrt{a^{2} - b^{2}}\) và tổng các khoảng cách từ mỗi điểm thuộc elip đó tới hai tiêu điểm bằng \(2a\).
- Phương trình \((2)\) được gọi là phương trình chính tắc của elip tương ứng.
Tính chất và hình dạng của Elip
Cho elip có phương trình chính tắc \(\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} =
1\), với \(a > b >
0\).
- Trục đối xứng \(Ox\), \(Oy\)
- Tâm đối xứng \(O\).
- Tiêu điểm \(F_{1}( - c;0),\
F_{2}(c;0)\).
- Tọa độ các đỉnh \(A_{1}( - a;0),\
A_{2}(a;0),\ B_{1}(0; - b),\ B_{2}(0;b)\).
- Độ dài trục lớn \(2a\). Độ dài trục bé \(2b\).
- Nội tiếp trong hình chữ nhật cơ sở có kích thước là \(2a\) và \(2b\).
- Tâm sai \(e = \frac{c}{a} <
1\).
- Hai đường chuẩn \(x = \frac{a}{e}\) và \(x = - \frac{a}{e}\).
- \(M(x;y) \in (E)\). Khi đó \(MF_{1} = a + ex\): bán kính qua tiêu điểm trái.
- \(MF_{2} = a - ex\): bán kính qua tiêu điểm phải.
2. HYPEBOL
Trên mặt phẳng, nếu hai thiết bị đặt tại các vị trí \(F_{1}\),\(F_{2}\) nhận được một tín hiệu âm thanh cùng lúc thì vị trí phát ra tín hiệu cách đều hai điểm \(F_{1}\),\(F_{2}\), và do đó, nằm trên đường trung trực của đoạn thẳng \(F_{1}F_{2}\).
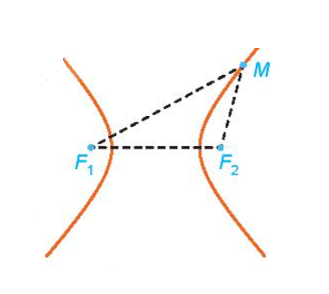
Cho hai điểm phân biệt cố định \(F_{1}\), \(F_{2}\). Đặt \(F_{1}F_{2} = 2c\). Cho số thực dương \(a\) nhỏ hơn \(c\). Tập hợp các điểm \(M\) sao cho \(\left| MF_{1} - MF_{2} \right| = 2a\) được gọi là đường hypebol. Hai điểm \(F_{1}\), \(F_{2}\) được gọi là hai tiêu điểm và \(F_{1}F_{2} = 2c\) được gọi là tiêu cự của hypebol đó.
Phương trình Hypebol
Trong mặt phẳng tọa độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn thẳng nối hai tiêu điểm đó thì có phương trình \(\frac{x^{2}}{a^{2}} -
\frac{y^{2}}{b^{2}} = 1\), với \(a,b
> 0\).
Ngược lại, mỗi phương trình có dạng \((4)\) đều là phương trình của hypebol có hai tiêu điểm \(F_{1}\left( - \sqrt{a^{2} +
b^{2}};0 \right)\), \(F_{2}\left(
\sqrt{a^{2} + b^{2}};0 \right)\), tiêu cự \(2x = 2\sqrt{a^{2} + b^{2}}\) và giá trị tuyệt đối của hiệu các khoảng cách từ mỗi điểm thuộc hypebol đến hai tiêu điểm bằng \(2a\).
Phương trình được gọi là phương trình chính tắc của hypebol tương ứng.
3. PARABOL
Cho một điểm \(F\) cố định và một đường thẳng \(\Delta\) cố định không đi qua \(F\). Tập hợp các điểm \(M\) cách đều \(F\) và \(\Delta\) được gọi là đường parabol.
Điểm \(F\) được gọi là tiêu điểm, \(\Delta\) được gọi là đường chuẩn, khoảng cách từ \(F\) đến \(\Delta\) được gọi là tham số tiêu của parabol đó.
Phương trình Parabol
Xét \((P)\) là một parabol với tiêu điểm \(F\), đường chuẩn \(\Delta\). Gọi \(H\) là hình chiếu vuông góc của \(F\) trên \(\Delta\). Khi đó, trong hệ trục tọa độ \(Oxy\) với gốc \(O\) là trung điểm của \(HF\), tia \(Ox\) trùng với tia \(OF\), parabol \((P)\) có phương trình:
\(y^{2} = 2px\) \((5)\)
Phương trình \((5)\) được gọi là phương trình chính tắc của parabol \((P)\).
Ngược lại, mỗi phương trình dạng \((5)\), với \(p
> 0\), là phương trình chính tắc của parabol có tiêu điểm \(F\left( \frac{p}{2};0 \right)\) và đường chuẩn \(\Delta:x = -
\frac{p}{2}\).
-----------------------------------------
Trên đây là toàn bộ kiến thức trọng tâm về ba đường Conic: Elip, Hypebol, Parabol trong chương trình Toán lớp 10. Hy vọng bài viết giúp bạn nắm vững định nghĩa, tính chất, dạng phương trình và phương pháp nhận dạng từng loại Conic. Hãy tiếp tục theo dõi website để cập nhật thêm nhiều chuyên đề Toán 10 chi tiết, có hệ thống và phù hợp cho ôn kiểm tra, ôn thi học kì.
